НЕЗАЛЕЖНИХ ВИПРОБУВАНЬ
1. Схема Бернуллі. Формула Бернуллі.
2. Найімовірніше число.
3. Формула Пуассона.
Задача. Із партії, в якій 12 стандартних і 4 нестандартні деталі, навмання беруться 3 деталі з поверненням. Знайти ймовірність того, що серед узятих деталей:
1) усі три стандартні;
2) не більш як одна нестандартна;
3) принаймні одна нестандартна.
Розв’язання. Маємо схему трьох незалежних випробувань. Нехай подія А – „узята щоразу деталь стандартна“, тоді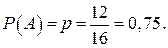 
Імовірності обчислюватимемо за формулою Бернуллі:
1) 
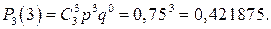
2) Подію «із трьох деталей не більш як одна нестандартна» можна розглядати так: узято 3 стандартні деталі або 2 стандартні і одну нестандартну деталь. У позначеннях формули Бернуллі
3) Протилежною для даної буде подія «усі три деталі стандартні». Їй рівносильна подія 
Обчислимо цю ймовірність: 
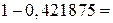
Задача. Частка довгих волокон у партії бавовни становить у середньому 0,6 загальної кількості волокон. Скільки потрібно взяти волокон, щоб найімовірніше число довгих волокон серед них дорівнювало 40?
Розв’язання. Скористаємося формулою, за якою визначається найімовірніше число:
Підставимо сюди значення відомих величин:
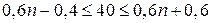
Задача має два розв’язки: n = 66 i n = 67.
Задача. Завод відправив на базу 1000 доброякісних виробів. За час перебування в дорозі кожний виріб може бути пошкоджено з імовірністю 0,003. Знайти ймовірність того, що на базу прибудуть 3 пошкоджені вироби.
Розв’язання. Якщо подія А – «виріб пошкоджено», то її ймовірність р = = 0,003. Розглядається схема незалежних випробувань, n = 1000. Імовірність події А досить мала, тому задачу розв’яжемо за формулою Пуассона:
Виконуючи обчислення, знаходимо: 
Відповідну ймовірність можна знайти за таблицею при 
, 
.
ПРАКТИЧНЕ ЗАНЯТТЯ 5. ПОСЛІДОВНІСТЬ
НЕЗАЛЕЖНИХ ВИПРОБУВАНЬ
1. Локальна теорема Муавра-Лапласа. Функція Гаусса. Її властивості.
2. Інтегральна теорема Муавра-Лапласа. Функція Лапласа. Її властивості.
Задача. На кожні 40 відштампованих виробів у середньому припадає 4 дефектних. Із усієї продукції навмання узято 400 виробів. Знайти ймовірність того, що серед них 350 виробів будуть без дефектів.
Розв’язання. Подія А – «узято виріб без дефекту». За умовою Р (А) = р = 0,9. Проведено n = 400 незалежних випробувань. Розв’яжемо задачу за формулою локальної теореми Лапласа:
Підставляючи дані за умовою задачі, дістаємо: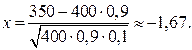 
За таблицями знаходимо 
беручи до уваги, що 
– парна функція.
Отже, 
Задача. Зерна пшениці проростають з імовірністю 0,95. Знайти ймовірність того, що із 2000 посіяних зерен зійде від 1880 до 1920.
Розв’язання. Подія А – «зерно пшениці зійшло». Її імовірність р = 0,95, кількість незалежних випробувань n = 2000. Застосуємо формулу інтегральної теореми Лапласа:
де 
– функція Лапласа, а далі виконаємо обчислення:
Значення функції Лапласа беруться з відповідної таблиці.
Задача. Верстат-автомат виготовляє стандартну деталь з імовірністю 0,9. Із продукції беруть партію деталей. Скільки деталей має містити партія, щоб з імовірністю 0,9973 можна було стверджувати: у партії відхилення відносної частоти появи нестандартної деталі від імовірності її виготовлення не перевищуватиме 0,03? Визначити можливу кількість нестандартних деталей у партії за даних умов.
Розв’язання. Подія А – «виготовлено нестандартну деталь». Маємо схему з n незалежними випробуваннями, в якій 
Скористаємося формулою:
За таблицями знаходимо 
Визначимо кількість нестандартних деталей у партії за даних умов, розв’язавши нерівність:
Отже, у партії із 900 деталей буде від 63 до 117 нестандартних деталей.
Задача. Маємо три партії деталей. Перша складається з 9 стандартних і 3 нестандартних; друга – із 12 стандартних і 3 нестандартних; третя – із 18 стандартних і 9 нестандартних деталей. Із кожної партії навмання беруть по одній деталі. Знайти ймовірність того, що в партії буде 0, 1, 2, 3 стандартні деталі.
Розв’язання. Подія А – «поява стандартної деталі в кожному випробуванні». Позначимо через 
імовірності узяття стандартної деталі із і -ї партії. Для обчислення ймовірностей складемо твірну функцію:
Отже, 
