Практичне заняття 8. Неперервна випадкова

ВЕЛИЧИНА

 

Приклад. Неперервна випадкова величина Х має закон розподілу ймовірностей у вигляді трикутника, зображеного на рис. 5.

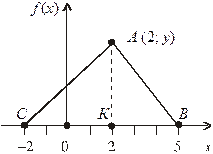
Рис. 5

Записати вирази для щільності ймовірностей і функції розподілу ймовірностей. Побудувати графік F (x) і обчислити Р (0 < X < 4).

Розв’язання. На проміжку [–2; 2] щільність ймовірностей змінюється за законом прямої пропорційної залежності f (x) = k ₁ x + b ₁ (k ₁> 0), а на проміжку [2; 5] за аналогічним законом f (x) = k ₂ x + b ₂ (k ₂< 0). Для знаходження значень параметрів k ₁, b ₁, k ₂, b ₂ обчислимо координати вершини цього трикутника А (х, у). Абсциса цієї точки відома за умовою задачі: х = 2; ординату знаходимо за умовою нормування, згідно з якою площа цього трикутника АВС має дорівнювати одиниці:

Отже, шукані координати:

Знаходимо рівняння прямої, яка проходить через точки С (–2; 0) і :

 

 

Отже, на проміжку [–2; 2] маємо:

Рівняння прямої, що проходить через точки :

Звідси на проміжку [2; 5] дістаємо:

Отже, на проміжку [–2; 5] щільність ймовірностей

Знаходимо F (x) на обох розглядуваних проміжках:

1) на проміжку [–2; 2]:

2) на проміжку [–2; 5]:

Отже, функція розподілу ймовірностей

Графік F (x) зображено на рис. 6.

Рис. 6

Обчислюємо ймовірність події 0 < X < 4 згідно з (65) і (72).

На інтервалі [0; 4] діють два закони розподілу:

1)

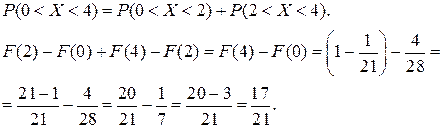
Отже, .

 

Приклад. Дано щільність ймовірностей

Обчислити М (Х).

Розв’язання.

 

Приклад. За заданою функцією розподілу ймовірностей

обчислити М (Х).

Розв’язання. Для обчислення М (Х) необхідно знайти щільність ймовірностей

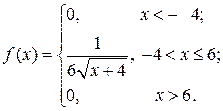
Тоді:

ПРАКТИЧНЕ ЗАНЯТТЯ 9. НЕПЕРЕРВНА ВИПАДКОВА

ВЕЛИЧИНА

Приклад. Задано щільність імовірностей:

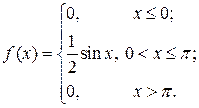
Обчислити D (X); s (X). Знайти Мо; Ме.

Розв’язання.

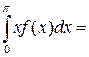
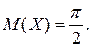
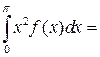
Графік f (x) зображено на рис. 7.

Рис. 7

Оскільки є максимальним значенням, то

Знаходимо F (x) =

Отже,

.

Приклад. Задано щільність ймовірностей (рис 8).

Рис. 8

Обчислити D (X); s (X); Mе. Знайти Мо.

Розв’язання. За умовою нормування знайдемо ординату точки В:

.

На проміжку [–2; 0] .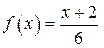

На [0; 4] .

Отже, щільність ймовірностей

Знаходимо функцію розподілу ймовірностей:

На проміжку [–2; 0]

На [–2; 4]

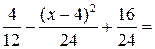
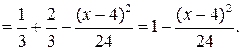
Отже, функцію розподілу ймовірностей можна подати у вигляді

Графік F (x) зображено на рис. 9.

Рис. 9

Далі обчислюємо D (X):

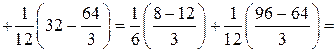
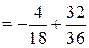
Для визначення Ме необхідно знайти проміжок, в якому вона міститься. Оскільки то медіана належить проміжку [0; 4].

Далі маємо:

Отже, Ме = Мо = 0.

Приклад. Задано щільність ймовірностей:

Обчислити Аs, Еs.

Розв’язання.

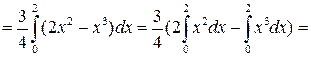
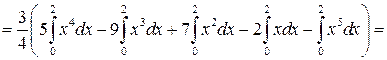
Оскільки m₃ = 0, то і Аs = 0. Отже, можливі значення випадкової величини Х симетрично розподілені відносно М (Х) = 1. Для обчислення Еs необхідно знайти m₄ і s.