МНОЖЕННЯ ЙМОВІРНОСТЕЙ
1. Теореми додавання ймовірностей.
2. Теореми множення ймовірностей.
Задача. Партія містить 12 стандартних і чотири нестандартні деталі. Навмання беруть три деталі. Знайти ймовірність того, що серед узятих деталей:
1) не менш як дві стандартні;
2) усі три нестандартні;
3) принаймні одна стандартна.
Розв’язання. 1) Нехай подія А – «серед трьох узятих деталей не менш як дві стандартні». Тоді її можна подати як суму двох подій: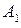 
– «серед трьох узятих деталей дві стандартні і одна нестандартна» і 
– «усі три узяті деталі стандартні». Події 
несумісні, тому маємо:
Імовірності подій 
знайдемо згідно з класичним означенням імовірності.
Отже, 
2) Подія В – «усі три взяті деталі нестандартні». Цю подію можна подати як добуток трьох подій 
де і -та деталь нестандартна, 
Умовою задачі не задано, що деталі беруться з поверненням. Отже, взяти три деталі разом – це те саме, що брати їх по одній без повернення, а тому події залежні. Згідно з цим імовірність події В обчислюємо так:
3) Подія С – «із трьох деталей принаймні одна стандартна». Протилежна подія 
– «усі три деталі нестандартні». Імовірність цієї події щойно знайдено: 
. Остаточно маємо: 
Задача. Маємо 3 партії деталей. Перша партія складається з 10 стандартних і 3 нестандартних деталей, друга – із 15 стандартних і 4 нестандартних, третя – із 20 стандартних і 5 нестандартних деталей. Із кожної партії беруть по одній деталі. Знайти ймовірність того, що серед узятих деталей:
1) тільки одна стандартна;
2) тільки дві стандартні.
Розв’язання. Нехай згідно з умовою з кожної партії взято по одній деталі. При цьому можуть відбутися події 
, які полягають відповідно в тому, що деталь, яку взяли з першої, другої і третьої партії виявилась стандартною.
1) Подія А – «тільки одна із трьох деталей виявилась стандартною». Цю подію можна подати так: 
Групи подій, сумою яких є подія А, несумісні між собою, а події в кожній групі незалежні. Тому ймовірність події А обчислимо так:
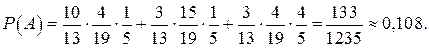
2) Подія В – «тільки дві деталі із трьох виявились стандартними». Подамо цю подію через події 
та протилежні до них:
Подію В подано як суму несумісних груп подій. У кожній групі події незалежні. Знайдемо ймовірність події В:
Задача. Перевезення вантажів для підприємства забезпечують два автогосподарства, які з цієї метою щодня в першу зміну мають виділяти по одному автомобілю. Імовірність виходу автомобіля на лінію в першому автогосподарстві дорівнює 0,7, а в другому – 0,6. Знайти ймовірність того, що в першу зміну на підприємстві перевозитимуться вантажі.
Розв’язання. Розглянемо події: А – «на підприємстві в першу зміну перевозитимуться вантажі»; 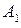– «для перевезення вантажів прибув автомобіль із першого автогосподарства»; – «для перевезення вантажів прибув автомобіль із другого автогосподарства». Тоді 
Події 
сумісні, тому 
Очевидно, що події незалежні і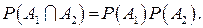 
Остаточно дістаємо:
Задача. Прилад складається із трьох вузлів, які працюють незалежно один від одного, причому другий і третій вузли взаємозамінювані. Ймовірності виходу з ладу вузлів на заданому часовому проміжку становлять відповідно 0,2; 0,3 і 0,4. Знайти ймовірність того, що протягом заданого часу прилад працюватиме.
Розв’язання. Розглянемо події: А – «прилад працює протягом заданого часу»;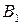 
– «перший вузол працює»; 
– «другий вузол працює»; 
– «третій вузол працює». Подія А настає, якщо працюють перший та другий вузли, або перший та третій вузли, або всі три вузли разом. Звідси: 
За умовою задачі маємо, що події 
незалежні, а події 
– сумісні. Тому
Під час обчислення враховано, що умовою задачі задано ймовірності протилежних подій.
Задача. Ймовірність того, що справним є перший комп’ютер 
, другий – 
,третій 
.Знайти ймовірність того, що справними є принаймні два комп’ютери.
Розв’язання. Нехай 
– подія, яка полягає в тому, що перший комп’ютер справний, 
– подія, яка полягає в тому, що другий комп’ютер справний,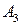 
– подія, яка полягає в тому, що третій комп’ютер справний, 
– подія, яка полягає в тому,що справними є принаймні два комп’ютери.
Виразимо подію через події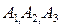 
,а також події їм протилежні.
Використовуючи теореми додавання та множення ймовірностей, маємо
