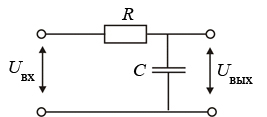
Интегрирование в математическом плане является операцией, обратной дифференцированию. Реализующая функцию интегрирования пассивная цепь (интегрирующая цепь (ИЦ), рис. 2.5) очень похожа на ДЦ, однако элементы R и C в схемах ДЦ и ИЦ переставлены местами. В ИЦ U выx = UC. При подаче на вход ИЦ видеоимпульса прямоугольной формы положительной по-
|
| Рис. 2.5 |
лярности, имеющего амплитуду U 0 и длительность τи, конденсатор будет заряжаться, зарядный ток потечет через сопротивление R. После окончания входного импульса (начиная с момента τи) конденсатор разряжается. Таким образом, процессы в пассивных ДЦ и ИЦ полностью совпадают. Различие заключается лишь в том, напряжение на каком элементе схемы является выходным. Преобразование импульсов интегрирующей цепью иллюстрируют диаграммы напряжений рис. 2.6 (а – случай τи > 3 RC; б – τи < 3 RC).
Рис. 2.6
Для обеспечения высокого качества интегрирования необходимо заряжать конденсатор как можно медленнее, так как только начальный участок экспоненты близок к линейной функции (интегралом от постоянной величины является линейная функция). Ошибка интегрирования [%] определяется как εи = (τи /3τ)100. Эта формула является обратной по отношению к выражению для εд. К сожалению, улучшение качества интегрирования в пассивной ИЦ сопровождается снижением амплитуды U выx, и при очень малых εи сигнал может быть утрачен.
Пассивная ИЦ при подаче на ее вход гармонического сигнала выполняет функции фильтра низких частот (ФНЧ). Как и в ДЦ, резистор R и XC образуютделитель из двух сопротивлений, но в ИЦ коэффициент деления равен (− jXC)/(R − jXC). При f = 0 XC → ∞, поэтому коэффициент передачи делителя равен 1, при f → ∞ XC = 0, конденсатор шунтирует выход схемы и КU = 0. Так же как и ДЦ, ИЦ является фазовращателем (ФВ), обеспечивающим набег фаз в пределах Δφ = 0…60º, извеном задержки на время до 1/6 периода гармонического сигнала.
Полосовой фильтр
Полосовой фильтр (ПФ) – схема, пропускающая сигналы со входа на выход в определенной полосе частот, но имеющая нулевой коэффициент передачи при более низких и более высоких частотах.
Полосовой фильтр получают последовательным соединением ФВЧ и ФНЧ, при этом безразлично, в каком порядке они следуют. Дополнительным условием при этом является соблюдение неравенства f гр ФНЧ > f гр ФВЧ. Если оно не будет выполнено, то через схему не пройдут никакие сигналы (часть не пропустит ФНЧ, другую часть – ФВЧ).
Применительно к полосовым фильтрам вводят целый набор параметров, смысл которых поясняет рис. 2.7: две граничных частоты – нижнюю f н.гр и верхнюю f в.гр, при которых КU» 0,7 mах[ КU (f)]; диапазон частот Δ f = f в.гр − f н.гр называют полосой пропускания. Если Δ f << (f в.гр; f н.гр), т. е. схема является узкополосной, то как параметр используют отношение средней частоты полосы к ее ширине Q = f ср/Δ f = (f в.гр + f н.гр)/(2Δ f), называемое добротностью.
| 
|
| Рис. 2.7 | Рис. 2.8 |
Примером ПФ является мост Вина (рис. 2.8). Схема представляет собой резистивно-емкостный делитель с комплексным коэффициентом передачи.
Максимальное значение модуль КU имеет при f 0 = 1/(2p RC); | КU | = 1/3), при этом набег фаз в схеме отсутствует (Δφ = 0).
Режекторный фильтр
Режекторный фильтр (РФ) – схема, не пропускающая сигналы со входа на выход в определенной полосе частот, но имеющая близкий к единице коэффициент передачи при более низких и более высоких частотах.
Режекторный фильтр получают параллельным соединением ФВЧ и ФНЧ. Дополнительным условием при этом является соблюдение неравенства f гр ФНЧ < f гр ФВЧ. Если оно не будет выполнено, то через схему пройдут все сигналы (часть пропустит ФНЧ, другую часть – ФВЧ, а средние по частоте сигналы – оба фильтра).
Для режекторных фильтров используют те же параметры, что и для полосовых: две граничных частоты – нижнюю f н.гр и верхнюю f в.гр, при которых КU» 0,7 mах[ КU (f)]; однако диапазон частот Δ f = f в.гр − f н.гр называют полосой задержания. Отношение Q = (f в.гр + f н.гр)/(2Δ f) называют добротностью.
Примером ПФ является двойной Т-мост (рис. 2.9). Т-мостом схема называется потому, что по размещению элементов она напоминает букву «Т».
|
| Рис. 2.9 |
Двойным мостом схему называют потому, что вход и выход в ней соединены сразу двумя мостовыми структурами, одна из которых – ФНЧ (с резисторами в «перекладине» и конденсатором в «ножке»), другая – ФВЧ. Минимум коэффициента передачи имеет место при частоте f 0 = 1/(2p RC). Само значение КU при f = f 0 зависит от соотношения значений R и C в «перекладине» и «ножке»; наилучшая режекция достигается при соотношении n = 5 (при этом КU = 1/11).
Кварцевый фильтр
Примером неэлектрического фильтра является кварцевый фильтр (кварцевый резонатор, кварц), основой которого служит пластина, вырезанная из монокристалла двуокиси кремния SiO2. Эту пластину располагают между двумя металлическими обкладками, образующими кварцедержатель. В целом конструкция напоминает плоский конденсатор, однако благодаря свойствам кварцевой пластины характеристики кварцевого фильтра существенно отличаются от свойств емкости.
Эквивалентная электрическая схема кварцевого фильтра приведена на рис. 2.10. Собственно пластина может быть заменена последовательным сое-
|
| Рис. 2.10 |
динением параметров R, C и L. Кварцедержатель включен параллельно и обладает емкостью C 0 < C. В электрической схеме имеют место два резонанса: параллельный на частоте f пар = 1/(2p 
) и последовательный при f посл = 1/(2p 
). Так как C 0 < C,то f пар > f посл. На низких частотах кварцевый фильтр имеет большое сопротивление (так как в обеих параллельных ветвях схемы имеются емкости, сопротивление которых равно XC = 1/(2π fC)), сигналы через него не проходят. С увеличением частоты сопротивление снижается и достигает минимума при f посл. Затем, по мере приближения к параллельному резонансу, сопротивление кварцевого фильтра вновь возрастает и достигает максимума при f пар. При частотах выше f пар сопротивление вновь снижается, так ем-
|
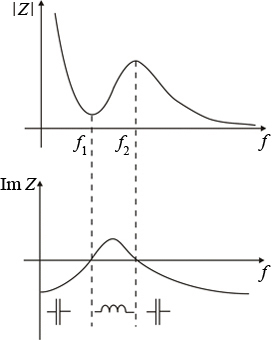
| Рис. 2.11 |
кость кварцедержателя постепенно превращается в короткое замыкание (емкость кварцевой пластины тоже уменьшается, но зато растет XL). Зависимость модуля сопротивления кварцевого фильтра Z изображена на рис. 2.11 (верхний график), там же приведена зависимость мнимой части Z от f (нижний график). На нижнем графике можно выделить области, в пределах которых кварцевый фильтр представляет собой эквивалентную емкость (Im Z < 0), а в узкой полосе частот между f посл и f пар Im Z > 0 и, следовательно, кварцевый фильтр имеет индуктивное сопротивление. Возможность заменить кварцем индуктивность представляет большой интерес в связи с постепенным устранением катушек индуктивности из электронных схем.
ЛИНИИ ЗАДЕРЖКИ
Способностью задержать сигнал обладают многие схемы – как рассмотренные ранее фильтры, в частности пассивные ДЦ и ИЦ, так и инвертирующие усилители, логарифмические преобразователи и т. д. Однако значение времени задержки Δ t з при этом невелико – не превосходит половину периода проходящего через схему гармонического сигнала. Большие значения Δ t з обеспечивают линии задержки (ЛЗ) – специальные электронные устройства, как электрические, так и неэлектрические. Линии задержки по своему принципу действия и конструкции подразделяются на три класса:
1) цепочечные (сосредоточенные) ЛЗ;
2) коаксиальные (распределенные) ЛЗ;
3) ультразвуковые ЛЗ (УЛЗ).
Цепочечные линии задержки
Цепочечные линии задержки представляют собой «гирлянды» из большого количества одинаковых конденсаторов и катушек индуктивности. Схема их соединения приведена на рис. 3.1. Благодаря тому, что напряжение
|
| Рис. 3.1 |
на емкости UC на 90º отстает от тока, а напряжение на индуктивности UL опережает ток на 90º, в каждом LC -звене удается получить набег фаз Δφ = 180º (рис. 3.2).
|
| Рис. 3.2 |
Результат достигается потому, что входной сигнал приложен сразу и к индуктивности, и к емкости, т. е. U вх = = UL + UC (фактически, с учетом противоположной направленности векторов UL и UC получается U вx = UL − UC). Выходной сигнал снимается с емкости, т. е. U выx = UC. Если UL > UC, что достигается подбором значений индуктивностей и емкостей, то векторы U вx и U выx противонаправлены. Задержка в одном звене цепочечной ЛЗ равна ; если ЛЗ содержит N однотипных звеньев, то Δ t з = N .
Наряду с временем задержки существенное значение имеет параметр, называемый волновым (или характеристическим) сопротивлением ρ. Знание ρ позволяет обеспечить оптимальное соединение ЛЗ с источником и получателем сигнала, избавиться от вредных явлений обратного распространения части сигнала вдоль линии и возникновения «эха». Для цепочечной ЛЗ ρ = 
.
Главным недостатком цепочечных ЛЗ является необходимость иметь большое количество (сотни – тысячи) однотипных индуктивностей и емкостей, параметры которых не должны иметь заметного разброса.
