R(квадрат) = [R(X,Y)]^2
То есть нужно просто коэффициент корреляции просто возвести в квадрат:-)
Билет № 58 Дано значение коэффициента корреляции между Yˆ и Y. Найти R2.
Формула для нахождения R2:
 ,
,
где  ,
,  .
.
Иными словами просто возводите этот коэффициент в квадрат.
На всякий случай формула коэффициента корреляции между Yˆ и Y:

Билет № 59 Дано уравнение парной линейной регрессии. Даны выборочные оценки дисперсии иксов и игреков. Найти R2.
Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):

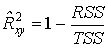 ,
,  , т.к. TSS = ESS + RSS
, т.к. TSS = ESS + RSS
 RSS =
RSS = 
TSS= 
ESS = 
TSS- Total Sum of Squares - полная сумма квадратов
ESS - Explained Sum of Squares - - «объясненная» сумма квадратов
RSS - Residual Sum of Squares - «оставшаяся» сумма квадратов
TSS= RSS+ ESS
или 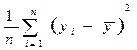 =
= 

или 
Тогда выражение для коэффициента детерминации можно представить в виде:


Даны значения RSS и ESS, число наблюдений и число предикторов в регрессии. Проверить гипотезу о качестве модели на основе статистики Фишера.
Дано значение R2, число наблюдений и число предикторов в регрессии. Проверить гипотезу о качестве модели на основе статистики Фишера.
Ho: R2= 0 vs H1: R2 не равно 0
для проверки значисмости R2 (выборочный) используется специальная статистика Фишера
f(R2 ) = F (статистика Фишера)
(**) F= ((ESS/ТSS) *1/k) / ((RSS/TSS) * 1/N-k) = ((1/k-1) * R2)) /((1/N-k) * (1- R2) )
k- число оцениваемых параметров модели (предикаторов)
N – число наблюдений
При верности Ho: F ~ F (k-1; N-k)
Распределение Фишера (связано с нормальным)
F (k,m) = (1/k * χ² (k)) / (1/m * χ² (m))
χ² (k) = ∑z², где Z ~ N (0,1) z – это стандартная нормальная величина

Считаем F по формуле (**), если попало в критическую зону, то R2 отличен от нуля
R2 =1, если наша регрессионная прямая прошла через все точки, хорошая модель
чем больше R2, тем лучше модель
Дан t-статистика, проверить гипотезу с помощью Фишера.
Гипотеза:
Н0: B0=0
H1: B1не равна 0.
Связь между F-критерием Фишераи t-статистикой Стьюдентавыражается равенством

Если tтабл < tфакт,то Hо отклоняется, т.е. а, b и rxy не случайно отличаются от нуля н сформировались под влиянием систематически действующего фактора x, Если tтабл > tфакт то гипотеза Нo не отклоняется
Дана таблица дисперсионного анализа. Заполнить пропуски в таблице.
Таблица состоит из значений TSS, RSS, ESS.
TSS (Total) = RSS (остатки) + ESS (модель регрессии)
TSS = ∑(yi – yсреднее)2
ESS = ∑(yкрышка – yсреднее)2
RSS = ∑(yi – yкрышка)2
reg dem_2000 cli gini_ye
Дана таблица выдачи регрессионного анализа. Запишите полученное уравнение регрес-сии
Source | SS df MS Number of obs = 25
-------------+------------------------------ F(2, 22) = 13.86
Model | 6.88491132 2 3.44245566 Prob > F = 0.0001
Residual | 5.46595999 22.248452727 R-squared = 0.5574
-------------+------------------------------ Adj R-squared = 0.5172
Total | 12.3508713 24.514619638 Root MSE =.49845
------------------------------------------------------------------------------
dem_2000 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
cli |.3920828.0807622 4.85 0.000.2245922.5595733
gini_ye |.0022019.0182327 0.12 0.905 -.0356105.0400143
_cons | -.7912347.7457838 -1.06 0.300 -2.337896.7554263
------------------------------------------------------------------------------
Уравнение регрессии:
dem_2000 = - 0,79 + 0,39*cli + 0,002*gini_ye + εi
65,66
67. Какова природа проблемы мультиколлинеарности в задачах множественной регрессии?
Природа проблемы мультиколлинеарности заключается в наличии сильных корреляционных связей между независимыми переменными, которые приводят к линейной зависимости нормальных уравнений.
68.К чему ведет мультиколлинеарность?
Мультиколлинеарность — наличие линейной зависимости между независимыми переменными регрессионной модели. При этом различают полную коллинеарность, которая означает наличие тождественной линейной зависимости переменных и мультиколлинеарность — наличие сильной корреляции между переменными.
Если полная коллинеарность приводит к неопределенности значений параметров, то частичная мультиколлинеарность приводит к неустойчивости их оценок. Неустойчивость выражается в увеличении статистической неопределенности — дисперсии оценок. Это означает, что конкретные результаты оценки могут сильно различаться для разных выборок несмотря на то, что выборки однородны
69.Назовите хотя бы 1 способ выявления мультиколлинеарности:
- Исследоване матрицы Х'Х. Если определитель матрицы Х'Х близок к нулю, то этосвидетельствует о наличии мультиколлинеарности.
- Анализ матрицы коэффициентов парной корреляции. Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,8






