Преимущества коэффициента корреляции Спирмена:
- высокая робастность (устойчивость к нетипичным наблюдениям)
- широкая область применения
Недостатки коэффициента корреляции Спирмена:
- не показывает конкретную функциональную связь между двумя переменными
- по большему счету подходит только для фиксации монотонной связи
14. Пусть на основе эмпирических данных вы получили, что R = 0,15 (это коэффициент корреляции Пирсона). Требуется понять, можно ли на основании этого результата утверждать, что на самом деле есть корреляция между иском и игреком. Как это сделать? Дайте ответ, если число наблюдений n = 25.
Решение:
1. H0: Corr (X,Y) = 0 vs. H1: Corr (X,Y)  0
0
2. 
3. 
 t(n-2)
t(n-2)
4. Считаем и подставляем в формулу. Потом смотрим по распределению Стьюдента.
15. Пусть на основе эмпирических данных вы получили, что р = 0,15 (где р = коэффициент корреляции Спирмена). Требуется понять, можно ли на основании этого результата утверждать, что на самом деле есть корреляция между иксом и игреком. Как это сделать? n = 25.
Решение:
1. H0: Corr (X,Y) = 0 vs. H1: Corr (X,Y)  0
0
-

-
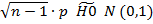
- Считаем и смотрим ответ. Если он лежит в интервале от -1,96 до 1,96, то H0 верна.
16. Для решения какой задачи применяется кластерный анализ?
Кластерный анализ решает задачу разбиения заданной выборки объектов на подмножества-кластеры таким образом, чтобы каждый кластер состоял из схожих объектов, а объекты из разных кластеров имели между собой как можно более существенные отличия. Главная цель – нахождение групп схожих объектов в выборке.
17. Укажите информацию, требующуюся исследователю «на входе» для решения задачи кластеризации.
1. Массив р-мерных наблюдений.
2. Априорные представления о классах.
3. Ожидаемые размеры и число кластеров.
18. Укажите, что является результатом кластеризации (что получается «на выходе»).
На «выходе» мы имеем правило классификации, позволяющее наилучшим в определенном смысле образом разбить имеющиеся р-мерные наблюдения на однородные в определенном смысле группы.
19. Какие виды кластерного анализа вам известны?
Иерархические (делятся на агломерационные и дивизивные) и неиерархические.
20. Как называется графические отражения алгоритма иерархической кластеризации?
1. Дендрограмма
2. Icicle plot (вертикальный и горизонтальный варианты).
21. Сформулируйте свойства, которым должно удовлетворять любое расстояние. Какое из этих свойств выполняется не всегда (например, в психологических исследованиях)?
1) d (O i, O j) > = 0
2) d (O i, O i) = 0
3) d (O i, O j) = 4*) d (O i, O j)= d (O j, O i)
Три свойства расстояния
1) Расстояние всегда положительно.
2) Сумма расстояний от a до b и от b до c равна расстоянию от a до c.
3) Расстояние от a до b равно расстоянию от b до a. (выполняется не всегда)
22. Какие виды метрики (расстояний) Вам известны?
1. Расстояние Евклида
2. Расстояние Манхеттена
3. Расстояние Чебышева
4. Квадрат расстояния Евклида
23. Даны 2 четырехмерных наблюдения (2 точки в четырехмерном пространстве). Вычислите между ними расстояния: Евклида, Манхеттен, Чебышёва.
Расстояние Евклида: dist = 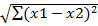
Расстояние Манхеттен: dist = 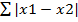
Расстояние Чебышева: dist = Max 
Q1 = x1(1) Q2 = x2(1)
x1(2) x2(2)
x1(3) x2(3)
x1(4) x2(4)
1) Расстояние Евклида:
dев=√ (x1(1) -x2(1))2 + (x1(2) -x2(2))2 +(x1(3) -x2(3))2 +(x1(4) -x2(4))2 (все под корнем)
2) Расстояние Манхетен
dман= ∣x1(1) -x2(1)∣ + ∣x1(2) -x2(2)∣+ ∣x1(3) -x2(3)∣+ ∣x1(4) -x2(4)∣
3) Расстояние Чебышёва
dчеб= max ⎨∣x1(1) -x2(1)∣ + ∣x1(2) -x2(2)∣+ ∣x1(3) -x2(3)∣+ ∣x1(4) -x2(4)∣⎬(из всех разностей выбирается наибольшая, которая и является расстоянием)
24. В каком случае применение евклидова расстояния не имеет под собой теоретического основания (хотя может давать разумные результаты)?
Применять евклидово расстояние можно только тогда, когда корреляция между всеми признаками должна быть равна 0, если корреляция не 0, то нужно ортогонализировать пространство. 24. В каком случае применение евклидова расстояния не имеет под собой теоретического






