Сколько раз вертикальная палка пересечет ветви, столько и будет кластеров.
1 кластер: номера 5,18,6,15,26,4,20,1,2,9
2 кластер: номера 7,22,17,21,13,14,8,10
3 кластер: номера 11,19,23,16,25,12,3,24
28. Какие методы приведения к единой шкале Вы знаете? Даны 5 наблюдений. Приведите их к единой шкале измерения, используя линейное преобразование и z-шкалу.
Методы:
- Стандартизация. 
, где 
– среднее значение 
, а Sx = 
- Линейное преобразование в заданный диапазон значений.
, причем 
Если нужно «развернуть» шкалу, то:
, причем
29. Объясните, почему при кластеризации необходимо приводить все показатели к единой шкале измерения?
Показатели, не приведенные к единой шкале, будут оказывать влияние на метрику. Если первый показатель лежит в диапазоне от 1 до 10, а второй – от 200 до 500, то на результаты анализа влияние оказывать будет по большему счету только второй показатель. (Показатели, измеренные в разных шкалах будут оказывать влияние на метрику, когда один (самый маленький или самый большой, значительно отличающейся от др.) будет доминировать. То есть если у нас показатели измерены в десятках, а один в тысячах, и нас будет перекос в сторону последнего).
Укажите недостатки линейного преобразования как процедуры приведения показателей к единой шкале. Нарисуйте картинку, иллюстрирующую ситуацию, когда применение линейного преобразования окажется неудачным выбором.
Когда у нас есть скопление данных, то при помощи линейного преобразования мы сокращаем вариацию, снижаем значимость наблюдения.
Если ситуация до линейного преобразования была такой:
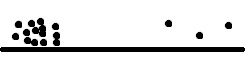
То после преобразования наблюдения, расположенные справа и близко друг другу спрессуются.
Это приводит к смещению R- квадрата и уменьшению значимости каждого наблюдения.
31. Почему не очень осмысленно применять алгоритмы кластерного анализа для классификации объектов в одномерном или двумерном пространстве?
Потому что там проще построить диаграмму рассеивания и посмотреть самим, какие получатся кластеры.
32. Как связаны понятия «регрессия игрека на икс» и «условное математическое ожидание игрека на икс»?
Регрессия игрека на икс – это «условное математическое ожидание игрека на икс» + остатки. «Условное математическое ожидание игрека на икс» - уравнение линейной регрессии в общем виде.
33. Какие соображения оправдывают использование линейных регрессионных моделей в качестве первого приближения заранее неведомых нам функций условного математического ожидания игрека на икс?
Гладкая ф-ция – это функция, непрерывно дифференцируемая на всей области определения. (Диф-ть – возможность подобрать производную). => Любая гладкая функция может быть хорошо приближена к линейной ф-ции (на некотором ограниченных диапозонах значений), то есть апроксимирована. Тк обычно из теории нельзя вывести точное значение функции – необходимо апроксимировать: строить линейную функцию, приближенную к гладкой.
34. Кто и почему впервые назвал регрессию регрессией?
Термин "регрессия" был введён Фрэнсисом Гальтоном в конце 19-го века. Гальтон обнаружил, что дети родителей с высоким или низким ростом обычно не наследуют выдающийся рост и назвал этот феномен "регрессия к посредственности". Сначала этот термин использовался исключительно в биологическом смысле. После работ Карла Пирсона этот термин стали использовать и в статистике.
Общее назначение множественной регрессии (этот термин был впервые использован в работе Пирсона - Pearson, 1908) состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной.
35. В чем суть метода наименьших квадратов?
МНК— один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.
Сущность:
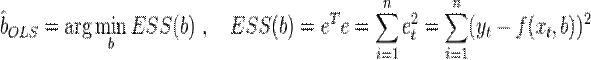Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов. Геометр. смысл. МНК - это ортогональн. проецир. игрека на икс.
