Центрирование переменных состоит в параллельном переносе системы координат по Х и/или по Y, при котором наклон (то есть) не меняется, но упрощается нахождение этого коэффициента. При центрировании Y, дополнительно, свободный член = 0.
Центрированный X =; EX = 0.
Формализация:
x1, x2 … xn – независимые переменные (регрессоры/предикторы)
y1, y2 … yn – зависимые переменные (отклики)
- общая форма парной линейной регрессии (в обычном случае), где - объясненная моделью часть, а - стандартные ошибки (та часть переменной, которую не удалось объяснить моделью). Построить регрессионную модель = оценить коэффициенты и.
В случае центрированных X мы меняем X на =>
Выведите МНК-оценки коэффициентов парной линейной регрессии (в случае центрированных иксов).
Для центрированных X:.
и = 0 => сокращаем.
38. Как получить МНК-оценки коэффициентов парной линейной регрессии в обычном случае центрированных иксов?
Пусть xi, yi – исходные данные, а; - центрированные X и Y.
Для центрированных X и Y:
Тогда для исходных данных:
Выведение МНК-оценок парной линейной регрессии в общем случае (то, что было на лекции):
· |: n (разделим на n)
Подставим во второе уравнение:
·
;; => подставим:
| * n
; => заменим:
39. Покажите связь между коэффициентом корреляции К.Пирсона и коэффициентом β1 парной линейной регрессии. (См рисунок в контакте)
Вопрос 40. Сформулируйте 4 условия Гаусса – Маркова.
1)E(ε1) = E(ε2) = … = E(εn) = 0, (15)
2)Var(ε1) = Var(ε2) = … = Var(εn) = σ2(16) - D(E/x) = сигма в квадрате - условная гомоскедастичность
3)Cov(xi,εj) = 0 при всех значениях i и j (18) -отсутствие эндогенности в узком смысле; распределение Е не зависит от распределения Х
4)Cov(εi, εj) = 0 при i≠j(17)
Единственно-должна отсутствовать автокорреляция
Вопрос 41. Сформулируйте теорему Гаусса – Маркова
Пусть матрица Х коэффициентов уравнений наблюдений (6) имеет полный ранг, а случайные возмущения (8) удовлетворяют четырем условиям,
В этом случае справедливы следующие утверждения:
а) наилучшая линейная процедура (13), приводящая к несмещенной и эффективной оценке (11), имеет вид:
б) линейная несмещенная эффективная оценка (19) обладает свойством наименьших квадратов: 
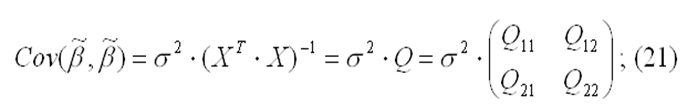
в) ковариационная матрица оценки (19) вычисляется по правилу:
г) несмещенная оценка параметра σ2 модели (2) находится по формуле:
Короче говоря, если выполняются 4 условия Гауса-Маркова, то МНК оценки являются несмещенными, состоятельными и наиб. Эффективными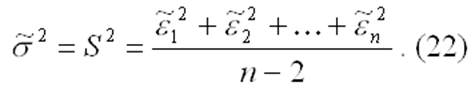 
среди всех линейных оценок.
Свойства точечных оценок
Несмещенность
Поскольку оценки являются случайными переменными, их значения лишь по случайному
совпадению могут в точности равняться характеристикам генеральной совокупности. Обыч-
но будет присутствовать определенная ошибка, которая может быть большой или малой, по-
ложительной или отрицательной, в зависимости от чисто случайных составляющих величин
х в выборке.
Желательно, чтобы математическое ожидание оценки равнялось бы соответствующей харак-
теристике генеральной совокупности. Если это так, то оценка называется несмещенной. Если
это не так, то оценка называется смещенной, и разница между ее математическим ожиданием
и соответствующей теоретической характеристикой генеральной совокупности называется
смещением.
Формальное определение:
Определение. Оценка q ˆ n параметра q называется несмещенной, если ее математическое
ожидание равно оцениваемому параметру при любом объеме выборки, т.е.
E (q ˆ n) = q.
В противном случае оценка называется смещенной.
Эффективность
Несмещенность — желательное свойство оценок, но это не единственное такое свойство.
Еще одна важная их сторона— это надежность. Мы хотели бы, чтобы наша оценка с макси-
мально возможной вероятностью давала бы близкое значение к теоретической характеристи-
ке, что означает желание получить функцию плотности вероятности, как можно более «сжа-
тую» вокруг истинного значения. Другими словами, оценка должна иметь малую дисперсию. Предположим, что мы имеем две оценки теоретического среднего, рассчитанные на основе
одной и той же информации, что обе они являются несмещенными и что их функции плот-
ности вероятности показаны на рис. 1. Поскольку функция плотности вероятности для оцен-
ки В более «сжата», чем для оценки А, с ее помощью мы скорее получим более точное значе-
ние. Эта оценка более эффективна.
Важно заметить, что мы использовали здесь слово «скорее». Даже хотя оценка В более эф-
фективна, это не означает, что она всегда дает более точное значение. При определенном
стечении обстоятельств значение оценки А может быть ближе к истине. Однако вероятность
того, что оценка А окажется более точной, чем В, невелика.
Мы говорили о желании получить оценку как можно с меньшей дисперсией, и эффективная
оценка — это та, у которой дисперсия минимальна. Таким образом, можно дать следующее
определение:
Определение. Несмещенная оценка q ˆ n параметра q называется эффективной, если она
имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра q
при заданном объеме выборки n.
Состоятельность
Состоятельной называется такая оценка, которая дает точное значение для
большой выборки независимо от входящих в нее конкретных наблюдений.
В большинстве конкретных случаев несмещенная оценка является и состоятельной. Можно
построить контрпримеры, но они, как правило, будут носить искусственный характер.
