Задамо центральну перспективну проекцію з центром проекції на початку координат, як показано на рис. 31. Для реальних обчислень необхідно також визначити значення мінімальної та максимальної відтинаючих площин по координаті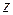 
: 
і 
, відповідно.
Границі екрана, або вікна виводу задають чотири відтинаючі площини зверху, знизу, справа та зліва. Отже, зображення, яке отримуємо за допомогою нашої проекції може знаходитися тільки всередині усіченої піраміди утвореної згаданими площинами, причому об’єкти зовні цієї піраміди не проектуються на екран, тобто є невидимими для спостерігача. Видимим об’ємом називається замкнута область простору, об’єкти всередині якої проектуються на екран. У випадку центральної перспективної проекції видимим об’ємом є усічена піраміда.
Рис 31. Видимий об’єм, вид збоку.
Однією з важливих задач комп’ютерної графіки є знахождення ефективного способу відсікання тривимірних об’єктів по границі видимого об’єму та видалення невидимих ребер і граней. Наприклад, у випадку центральної перспективи, для розв’язку задачі відтинання прийшлося би для кожної грані або ребра знаходити точки перетину із площинами відсіченої піраміди, що в загальному випадку потребувало би значних обчислень. Розв’язок полягає у перетворенні видимого об’єму до вигляду, в якому обчислення проводились би значно простіше. В загальному ідея полягає в тому, щоб звести перетворення центральної перспективи математично до вигляду паралельної проекції, в якій, очевидно, операція взяття проекції зводиться до простого відкидання у точок координати .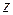
Будемо розв’язувати задачу в два етапи. Спочатку приведемо видимий об’єм до нормованого вигляду. При цьому значення 
, а границі по осям 
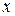і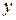 
лежать в діапазоні 
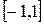, як показано на рис. 32.
Нормуючим перетворенням в цьому випадку буде операція масштабування, яка для довільної точки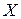 
виражається у вигляді:
,
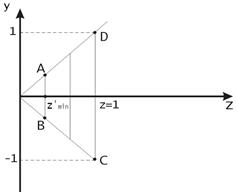
Рис. 32. Нормований видимий об’єм.
де 
, і відповідно, 
.
Нормований видимий об’єм дозволяє з великою легкістю розв’язувати задачу відсікання по границі. А саме, в цьому випадку може застосовуватися модифікований варіант алгоритму Коена-Сазарленда в якому замість 4-бітових використовуються 6-бітові коди зовні/всередині для опису знаходження точки у відповідній області простору. Рівняння бокових граней видимого об’єма сильно спрощуються, наприклад, для правої відтинаючої площини рівняння запишеться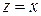 
, а для лівої бокової 
і т.д.. Тоді для деякої точки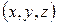 
умова встановлення біта в одиницю буде наступною:
1-й біт: 
2-й біт: 
3-й біт: 
4-й біт: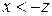 
5-й біт: 
6-й біт: 
Для ефективного розв’язку задачі видалення невидимих ребер/граней перетворимо нормований видимий об’єм до канонічного вигляду, як показано на рис. 33.
Рис. 33. Канонічний видимий об’єм.
Це досягається за допомогою матриці
.
Після застосування матриці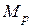 
нормований видимий об’єм стає прямокутним паралелепіпедом, що дозволяє перейти від центральної перспективної до паралельної проекції. Легко перевірити, що як показано на рис. 32, 33: 
, 
, 
, 
, а також, наприклад, 
.
Отже, нормуючи перетворення видимого об’єму можуть відбуватися за два кроки.
1 крок - перетворення до нормованого видимого об’єму та відсікання по 3-х мірному алгоритму Коена-Сазерленда.
2 крок – перетворення до прямокутного паралелепіпеда за допомогою матриці 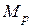і видалення скритих поверхонь при умові рівності координат 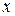і .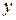
