Подібно тому, як двовимірні перетворення описуються матрицями розміром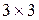 
, тривимірні перетворення можуть бути представлені матрицями розміром 
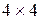. Тоді тривимірна точка 
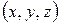записується в однорідних координатах як 
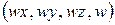, де 
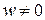. Для отримання декартових координат потрібно перші три однорідні координати розділити на 
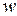. Два однорідних вектора описують одну декартову точку в тривимірному просторі, якщо 
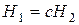, де 
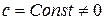и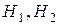 
- вектори, записані в однорідних координатах.
Матриці перетворень будемо записувати в правосторонній системі координат. При цьому додатній поворот визначається наступним чином. Якщо дивитися з додатної частини осі обертання (наприклад, осі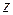 
) в напрямку початку координат, то поворот на 
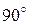проти годинникової стрілки буде переводити одну додатну напіввісь в іншу (вісь 
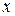в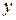 
, у відповідності з правилом циклічної перестановки).
Замітимо, що на практиці зручніше застосовувати лівосторонню систему координат, так як в цьому випадку зручніше інтерпретувати той факт, що точки з великими значеннями 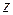знаходяться далі від спостерігача.
Запишемо тепер матрицю тривимірного переносу. Аналогічно двовимірному випадку.
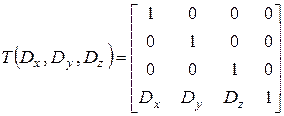, при цьому
.
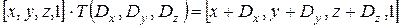Операція масштабування:
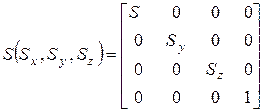
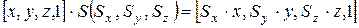
Перейдемо до операції повороту. Так як при двовимірному повороті в площині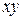 
координати 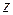залишаються незмінними, то поворот навколо осі 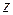записується так:
.
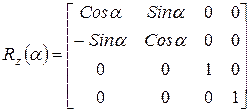Матриця повороту навколо осі 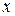має вигляд:
,
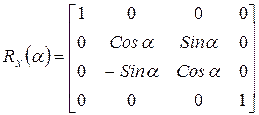і навколо осі :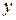
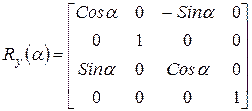
Зверніть увагу на зміну положення синуса кута з негативним знаком в матриці повороту навколо осі 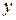. Правильність цих матриць легко перевірити поворотом одного з ортів на 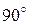, при цьому він повинен перейти в наступний по порядку орт на відповідній координатній осі.
Обернені перетворення будуть виражатися оберненими матрицями. Для операції переносу потрібно лише замінити знаки компонент вектора переносу на протилежні:
;
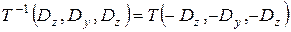для операції масштабування – на обернені значення:
;
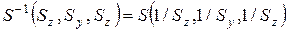для повороту – вибором негативного кута повороту:
.
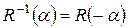Результатом декількох послідовних поворотів буде матриця
.
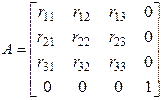Тут верхня матриця розміром 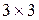називається ортогональною. Важливою її властивістю є те, що обернена до неї матриця є транспоновоною: 
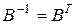. Це корисно тим, що при обрахунках достатньо поміняти індекси місцями та обернене перетворення отримується автоматично.
Після перемноження довільної кількості матриць вигляду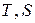 
та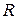 
результуюча матриця завжди буде мати вигляд:
.
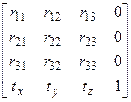Тут верхня частина розміром 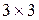визначає сумарний поворот і масштабування, а три коефіцієнти останнього рядка – сумарний перенос.
