Прямоугольное (равномерное) распределение — простейший тип непрерывных распределений. Если случайная переменная X может принимать любое действительное значение в интервале (а, b), где а и b – действительные числа, и если каждому значению случайной переменной соответствует одинаковая плотность вероятности, то переменная X имеет прямоугольное распределение. Иногда пользуются термином «равномерное распределение».
Из приведенного определения следует, что плотность распределения вероятностей этой случайной переменной должна быть постоянной, т. е. что в интервале (a, b) f(x) = с. Отсюда, а также из условия, что интеграл от функции f(x), взятый в интервале (а, b), должен равняться единице, нетрудно найти функцию плотности вероятности f(x). Имеем:
(4.1)
откуда cb – са = 1 и, следовательно, получим 
. Таким образом, функция плотности вероятности для прямоугольного распределения:
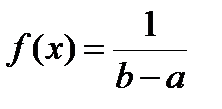для a ≤ x ≥ b. (4.2)
Для х > b и х < а плотность равняется нулю. Нетрудно вычислить математическое ожидание и дисперсию рассматриваемой случайной переменной. Имеем:
(4.3)
(4.4)
Отсюда находим, что дисперсия D2(X) равняется:
(4.5)
Прямоугольное распределение находит широкое применение в математической статистике. Оно имеет основополагающее значение для так называемых непараметрических методов – одного из новейших разделов статистики, находящего все более широкое применение. Понятием прямоугольного распределения иногда пользуются и в теории статистических оценок – в том разделе статистики, где изучаются методы построения выводов о значениях параметров в генеральной совокупности на основании случайной выборки. В некоторых теориях статистического вывода за исходный пункт принимается правило: что, если нам ничего неизвестно о значении оцениваемого параметра, то следует принять, что каждое его значение равновозможно. Это ведет к истолкованию оцениваемого параметра как случайной переменной, характеризующейся прямоугольным распределением.
Нормальное распределение
Нормальное распределение играет основную роль в математической статистике. Это ни в малейшей степени не является случайным: в объективной действительности весьма часто встречаются различные признаки, значения которых распределяются по нормальному закону.
Если число дискретных событий возрастает, график на рисунке 3.2, представляющий разложение бинома (p+q)n, все более приближается к плавной кривой. Это приближение имеет место и для p = q, и для
p 
q. В последнем случае скошенность кривой при возрастании n уменьшается. При приближении n к бесконечности график кривой приближается к симметричной кривой. Пределом такого приближения биномиального распределения является нормальное распределение, выраженное формулой и графически изображаемое на рисунке 4.1.
В этом качестве, а именно в качестве непрерывной формы для предела биномиального распределения, нормальное распределение было открыто для р = q в 1733 г. А. Муавром (Англия). Обобщение его для p q сделано П. Лапласом (Франция) и К. Гауссом (Германия) в начале XIX в. Это открытие привело во второй половине XIX века к особому подчеркиванию значения нормального «закона» как модели, которой следуют распределения результатов наблюдений во всех естественных явлениях. Английский ученый К. Пирсон в начале XX в. показал, что нормальное распределение является одним из многих типов распределений, имеющихся в природе. Значение нормального распределения вследствие этого снизилось в сфере наблюдений, но возросло в теоретическом отношении, особенно в области теории выборок.
Рисунок 4.1 – Нормальное распределение
Уравнение нормальной кривой выражает зависимость теоретических численностей f(x) или у от значений x – непрерывно распределяющейся случайной величины. Оно пишется в различных формах.
Выражение, являющееся основной формой, относится к кривой с площадью, равной единице:
(4.6)
В этом уравнении f(x) – теоретические численности, выраженные в долях единицы, или плотности вероятности случайного события x;
s – квадратическое отклонение данного нормального распределения; π и е известные константы, π = 3,1426, е = 2,7183, s – отклонение случайно распределенной величины X от средней арифметической m, являющейся центром распределения величины X.
Вычислим математическое ожидание нормальной случайной переменной. Согласно определению (2.5):
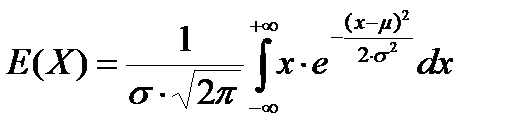(4.7)
Для вычисления этого интеграла введем новую переменную:
, 
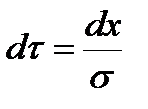. Получим:
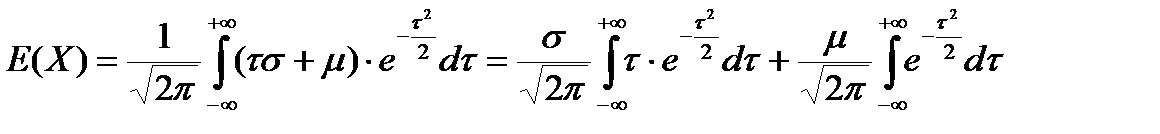(4.8)
Интегрируя по частям, находим, что первый из приведенных выше интегралов равняется нулю. Далее, из математического анализа известно, что интеграл функции 
, взятый в границах (–∞, + ∞), равняется 
. Таким образом, получаем:
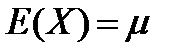(4.9)
Следовательно, параметр μ есть математическое ожидание нормальной случайной переменной, плотность вероятности которой дается формулой (4.6).
Для вычисления дисперсии предварительно точно так же находим значение Е (X2):
. (4.10)
Применив ту же подстановку, что при вычислении E(X), получим:
(4.11)
Интегрируя по частям, находим, что первый из интегралов в правой части формулы (4.11) равняется σ2, второй интеграл – нулю, а третий интеграл имеет значение μ2. Таким образом,
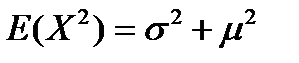, откуда 
Итак, дисперсия нормальной случайной переменной равняется σ2, а ее среднее стандартное отклонение – σ.
Для удобства расчетов отклонение переменной X от m обычно выражают в единицах среднего стандартного отклонения s.
Выражение 
называют нормированным отклонением и обозначают его буквой t.
Тогда уравнение кривой нормального распределения в нормированной форме будет:
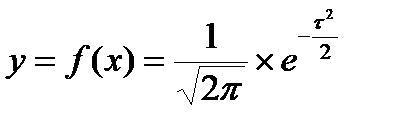(4.12)
Оно выражает зависимость между вероятностью y и нормированным отклонением t. Средняя такого распределения m равна нулю, а квадратическое отклонение s = 1. Графически кривая нормального распределения изображена на рисунке 4.1. Максимального значения у достигает в начале координат, т. е. в точке, соответствующей центру распределения, где Х = t = 0, s = 1.
Максимальная ордината, обозначим ее y0 = 1/2 × p = 0,39894. В других точках, т. е. при t ≠ 0, значения ординат y могут быть вычислены на основе формулы (4.12) путем логарифмирования.
На основе формулы (4.12) и данного анализа видно, что величина ординаты кривой нормального распределения может рассматриваться как функция нормированного отклонения t.
Кривая, показанная на рисунке 4.1, показывает, как плотности вероятностей (ординаты) растут до максимума в точке средней, т. е. в точке 0 и затем симметрично снижаются для значений у выше средней. Причем для X < m – 3s (или t < –3) и для X > m +3s
(или t > 3) ординаты уже незначительно отличаются от нуля. Это означает, что наиболее вероятны те значения X, которые близки к m. По мере удаления от m значения X становятся все менее вероятными. Причем одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной Х от m равновероятны.
В точках m – s и m + s кривая нормального распределения или кривая плотности нормального распределения вероятностей имеет перегибы.
При определении ординат для какого-либо конкретного частного распределения ординаты, полученные по формуле (4.12), умножают на N/σ, где N – общий объем численностей, σ – выборочное квадратическое отклонение в единицах измерения распределенной величины X.
При изучении распределений как теоретической базы статистических заключений наибольший интерес представляет площадь под нормальной кривой. Эту площадь можно представить как интеграл от функции (4.12). Если интегрирование провести от начала координат, т. е. от нуля до любого значения, получим значение площади, заключенной между у0 и значением у, соответствующим избранному τ. Математически функция площади от нормированного отклонения (обозначим ее F(t) при указанных пределах имеет выражение:
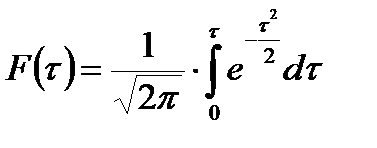(4.13)
При таком предположении и нормальном распределении в совокупности, выражаемом формулой 4.13, можно определить вероятности встретить любые значения исследуемых объектов, т. е получить сумму вероятностей по 4.13.
Этот интеграл относится к разряду неберущихся. Поэтому в литературе приведена четырехзначная таблица площади под нормальной кривой в долях единицы, за которую принята вся площадь под кривой, либо при расчетах можно воспользоваться следующей аппроксимацией:
F(t) = 0,0164 τ3 – 0,1564 τ2 + 0,4917 τ – 0,0119
Пример
Найдем теоретическую относительную численность, т. е. вероятность объектов, имеющих диаметр от Х1 = 12 до Х2 = 22 см, μ = 30 см, σ = 6 см. Стандартизованные отклонения двух указанных значений X будут:
τ1= (X1–μ)/σ = (12 – 30)/6 = –3, τ2 = (X2 – μ)/σ = (22 – 30)/6 = –1,33.
По таблице или представленной формуле F(–3) = 0,4986,
F(–1,33) = 0,4080. Отметим, что знак τ не имеет значения.
Разность F(τ1) – F(τ2) = 0,0904 означает вероятность встретить объекты указанного интервала X в общей совокупности, т. е. 9 объектов из 100.
Установим, пользуясь этим приемом, вероятности трех важных событий в теории выборок:
а) нормальная случайная переменная примет значение в интервале (μ – σ, μ + σ);
б) переменная примет значение в интервале (μ – 2σ, μ + 2σ);
в) она примет значение в интервале (–3σ, μ + 3σ).
Так как нормальная совокупность характеризуется μ = 0 и σ = 1, значения нормированного отклонения τ будут:
для а) –1, +1;
для б) –2; +2;
для в) –3, +3.
По таблице или формуле находим F(+1) = 0,3413, F(–1) = 0,3413, откуда вероятность события а), равная F(+l) + F(–l), составит 0,6826.
F(+2) = 0,4772, F(–2) = 0,4772, вероятность события б) равна 0,9544.
F(+3) = 0,4986, F(–3) = 0,4986, вероятность события в) равна 0,9972.
Эти результаты дают возможность утверждать, что в случае нормального распределения N (0; 1) 68% наблюдаемых значений отклоняются от среднего значения μ не более чем на величину стандартного отклонения σ, 95% значений не выйдут из пределов
μ ± 2σ и практически все значения уместятся в пределы μ ± 3σ. Вероятность отклонения за пределы 3σ равна 0,0026 ≈ 0,003, т. е. такое событие наступит только в среднем в 3 случаях из 1000 испытаний.
