Степень разнообразия особей в группе по изучаемому признаку измеряется несколькими показателями, из которых наибольшее значение имеет стандартное отклонение или стандартное отклонение:
(7.1)
(7.2)
s – стандартное отклонение;
x2 – сумма квадратов центральных отклонений, т. е. квадратов разностей между каждым значением и средней арифметической;
Xi – значение признака у каждого объекта в группе;
μ – средняя арифметическая признака для данной группы;
n – 1 – число степеней свободы, равное числу объектов в группе без одного.
Число степеней свободы
Число степеней свободы равно числу элементов свободного разнообразия в группе. Оно равно числу всех имеющихся элементов изучения без числа ограничений разнообразия.
Например, для исследования требуется взять три объекта с любым развитием изучаемого признака. В данном случае величина признака не имеет никаких ограничений, поэтому число степеней свободы n= 3 – 0 = 3.
Если требуется взять три числа с условием, что сумма их должна быть равна определенной величине, например: 100, то первое число может быть любой величины: 80, 800 и т. д., второе число также может быть выбрано свободно без всяких ограничений, например 10, 1269 и т. д., то третье же число может иметь только одно значение, такое, чтобы оно вместе с двумя предыдущими составило бы в сумме 100. Если два первых числа были 80 и 10, то третье должно быть 10; если два первых числа 800 и 1269, то третье должно быть отрицательным: –1969 (800+1269–1969 = 100).
В данном случае, при одном ограничении (сумма чисел должна быть равна 100), два числа выбираются свободно, а третье не имеет свободы выбора: для трех чисел имеются две степени свободы
n = 3 – 1 = 2.
Для n значений при k ограничениях имеется n = n–k степеней свободы.
При вычислении средней арифметической никаких ограничений величины значений признака не имеется. Поэтому число элементов, образующих среднюю арифметическую, равно числу вариантов.
При вычислении среднего квадратического отклонения имеется одно ограничение. Сигма вычисляется для определенной группы, имеющей определенную среднюю арифметическую. Поэтому разнообразие элементов, образующих стандартное отклонение, ограничено этим одним условием и в данном случае число степеней свободы равно числу вариантов без одного n = n–1.
Определение критерия достоверности разности 
двух средних величин производится при числе степеней свободы
n = n1+n2–2. Это связано с тем, что ошибка разности определяется на основе ошибок 
обеих средних, каждая из которых имеет число степеней свободы (для соответствующей сигмы) n–1. В сумме число степеней свободы:
n = n1–1+n2–1 = n1+n2–2
Для критерия достоверности разности двух коэффициентов корреляции число степеней свободы равно для первого коэффициента n1 = n1–2; для второго коэффициента n2 = n2–2; для их разности:
nd = n1+n2 = n1–2+n2–2 = n1+n2–4
По приведенным формулам можно рассчитывать стандартное отклонение для групп любого объема.
Стандартное отклонение служит основным показателем разнообразия значений признака в группе. Используется сигма и как самостоятельный показатель, и как основа для построения многих других показателей статистики: коэффициента вариации, ошибок репрезентативности, различных показателей распределения, коэффициентов корреляции и регрессии, элементов дисперсионного анализа, формул регрессии.
Основное свойство всякой группы – разнообразие входящих в нее объектов по изучаемому признаку – измеряется несколькими показателями. К ним относятся: лимиты и размах, стандартное отклонение, коэффициент вариации, квартили, децили, перцентили.
Следует иметь в виду, что формула сигмы с числом степеней свободы в знаменателе подкоренного количества применяется только для выборок:
(7.3)
Сигма генеральной совокупности вычисляется по формуле:
, (7.4)
где:
– генеральная сигма;
– генеральная средняя;
N – объем генеральной совокупности
Пример
На сельскохозяйственной выставке сравниваются экспонаты двух хозяйств, представивших лучшие экземпляры тыквы со своих огородов. Первое хозяйство представило 6 тыкв, весивших 33, 37, 32, 38, 34, 36 кг, второе представило 5 тыкв, весивших 33, 37, 34, 36, 35 кг.
Так как средний вес экспонатов оказался одинаковым у обоих экспонатов (μ1 = 35, μ2 = 35), было решено провести сравнение стандартности тыкв по среднему стандартному отклонению.
В данном случае сравнивались не выборки, а генеральные совокупности, так как оценка проводилась по выставочным экземплярам, которые целиком исчерпывали всю требующуюся в данном случае информацию.
Дисперсии и средние стандартные отклонения (сигмы):
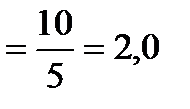(а не 
);
(а не 
).
; 
Коэффициенты вариации:
; 
.
Оказалось, что второй совхоз представил более стандартную партию тыкв.
Так как сравнение в данном случае проводилось по генеральным параметрам, то разность сигм заведомо достоверна и не нуждается в определении достоверности. Обычные методы определения достоверности разности в данном случае не нужны и неприменимы, так как сравниваемые группы выбирались не так, как это требуется при организации выборок (не рендомизированно).
Сравнение стандартности двух партий тыкв характеризует более благоприятно второе хозяйство, которое смогло подобрать более выровненную группу экспонатов.
Коэффициент вариации
Стандартное отклонение – величина именованная, выраженная в тех же единицах измерения, как и средняя арифметическая.
Поэтому для сравнения разных признаков, выраженных в разных единицах измерения, используется не абсолютное, а относительное значение среднего квадратического отклонения в форме коэффициента вариации:
, (7.5)
где:
V – коэффициент вариации;
σ – стандартное отклонение;
μ – средняя арифметическая.
Коэффициент вариации есть сигма, выраженная в процентах от средней арифметической. Этот показатель неименованный, поэтому он и пригоден для сравнения разных признаков или одного и того же признака, но в группах с резко различной средней величиной признака.
Пример
Если в стаде коров сводные показатели по удою за первую лактацию равны μ1 = 3000 кг, σ1 = 600 кг, а по живому весу μ2 = 400 кг, σ2 = 20 кг, то коэффициенты вариации будут иметь следующую величину:
по удою 
;
по живому весу 
Сопоставление коэффициентов вариации указывает на сильное разнообразие первотелок изученного стада по удою и слабое разнообразие их по живому весу.
В соответствии с этими характеристиками можно заключить, что в исследованном стаде имеются большие возможности отбора по удою (лучших – на племя, худших – на мясо), но слабые перспективы для подобного же отбора по живому весу.
Лимиты и размах
Для быстрой и примерной оценки степени разнообразия часто применяются простейшие показатели:
lim = {min ¸ max} – лимиты, т. е. наименьшее и наибольшее значения признака,
p = (max – min) – размах, или разность между лимитами.
Для группы данных 1, 2, 3, 4, 5 лимиты и размах могут быть обозначены так:
lim = l ¸ 5.
Иногда характеристика разнообразия группы в форме лимитов имеет столь большое производственное значение (например, при упаковке яблок, помидор и т. д., при оценке партии беконных тушек), что кладется в основу денежной оценки продукта.
При проведении параллельных анализов лимиты результатов и их размах служат показателем качества работы лаборанта.
В некоторых случаях лимиты могут служить единственной характеристикой признака.
7.1.4 Приближенные значения μ и s
Если не требуется особой точности, то на основе лимитов можно быстро определить приближенные значения средней арифметической и сигмы.
Средняя арифметическая примерно равна полусумме лимитов:
. (7.6)
Стандартное отклонение примерно равно разности лимитов, деленной на число K, зависящее от численности группы (n):
(7.7)
Число K можно находить по таблице 7.1.
Таблица 7.1 – Числа K, на которые надо разделить размах значений признака, чтобы получить примерное значение среднего квадратического отклонения
| n | 2 - 5 | 6 - 15 | 16 - 49 | 50 - 200 | 201 - 1000 | > 1000 |
| K |
Пример
Среди 20 выловленных волков максимальный вес животного оказался 42 кг, минимальный – 30 кг.
кг; 
кг.
Перечисленные свойства лимитов и размаха показывают, что эти простейшие показатели разнообразия представляют вполне реальный интерес даже при наличии и более точных показателей.
Нормированное отклонение
Обычно степень развития признака определяется путем его измерения и выражается определенным именованным числом: 3 кг веса, 15 см длины, 20 зацепок на крыле у пчел, 4% жира в молоке, 15 кг настрига шерсти, 700 г привеса в сутки и др. Этот основной способ характеристики признаков оказывается недостаточным, когда требуется еще и оценить полученное значение, т. е. определить, можно ли его считать значительным или, наоборот, недостаточным, или находящимся в норме.
Задачи подобного рода возникают очень часто как в научных работах, так и в производственных условиях.
Для решения таких задач применяется общий принцип: ценность особи определяется ее отношением к группе, что может быть измерено особым – показателем – нормированнным отклонением, вычисляемым по формуле:
, (7.8)
где:
– нормированное отклонение;
Xi – результат непосредственного измерения признака;
μ – средняя арифметическая соответствующей группы, из которой взята изучаемая особь;
s – стандартное отклонение этого признака в группе.
Нормированное отклонение показывает, на сколько сигм отклоняется значение признака от средней для соответствующей группы.
Нормированное отклонение – величина неименованная, что представляет большое удобство при сравнении развития различных признаков.
Пример
Если мальчик 14 лет имеет длину тела 159 см, обхват груди 64 см емкость легких 2070 см3, обхват головы 52 см и вес 40 кг, то по этим цифрам невозможно дать сравнительную характеристику развития разных частей тела и определить общий тип физического развития ученика.
Для этой цели необходимо сравнить индивидуальные показатели со средними характеристиками мальчиков этого возраста по среднему уровню каждого признака и его разнообразию в форме нормированного отклонения, что показано в таблице 7.2.
Таблица 7.2 – Оценка телосложения
| Показатели | Мальчик 14 лет | Все мальчики 14 лет | Нормированное отклонение
| |
| Xi | μ | s | ||
| Длина тела Обхват груди Емкость легких Обхват головы Вес | 8,5 4,0 2,0 6,0 | (+17) / 8,5= + 2,0 (–2) / 4,0 = – 0,5 (–230) / 460 = – 0,5 (+2) / 2 = + 1,0 0 / 6 = 0,0 |
Выяснилось, что рост мальчика на две сигмы, а обхват головы на одну сигму превышают средние показатели, вес – на среднем уровне, а емкость легких и обхват груди ниже среднего уровня на полсигмы. Очевидно, это – высокий, узкогрудый, большеголовый мальчик астенического типа.
