В этой теме рассмотрим основные типы распределения дискретных случайных переменных. Предположим, что вероятность наступления некоторого случайного события А при единичном испытании равно р. Производится серия испытаний в каждом из которых случайное событие А может наступить с этой вероятностью р, причем следует отметить, что испытания независимы друг от друга.
Примеры исчисления вероятностей можно обобщить на основе следующей ниже иллюстрации.
Если подбрасываются одновременно 2 монеты (а, b), то существуют 4 возможных случая выпадения герба Т и цифры Н:
аb аb аb аb
ТТ ТН НТ НН
В первом исходе имеем 2 герба. Принимая это за 2 благоприятных исхода, получим вероятность каждого из них р, а сложного события (ТТ)  . В данном случае, при р = 1/2;
. В данном случае, при р = 1/2;
p2 = 1/4.
Четвертый из возможных исходов НН представляет 2 неблагоприятных исхода с вероятностью q × q = q2 = 1/4.
Каждый из двух других исходов является комбинацией одного благоприятного и одного неблагоприятного случаев.
Вероятность каждого из этих исходов равна p × q = 1/2 × 1/2 =1/4, а обоих вместе ТН и НТ равна их сумме, т. е. 2 р × q = 1/2.
Обобщенным выражением процесса получения вероятностей различных сочетаний независимых событий, когда вероятности их известны, являются последовательные члены разложения бинома.
Для рассматриваемого примера из двух событий имеем:
(р +q)2 = p2 + 2pq + q2., При p = 1/2 получим (1/2 + 1/2)2 = 1/4+1/2+1/4.
Если 3 монеты а, b, с подбрасываются одновременно, получим 8 возможных комбинаций:
abс abc abc abc abc abc abc abc
ТТТ ТТН ТНН ТНТ НТТ НТН ННТ ННН
Вероятность выпадения 3 гербов составит 1/8, 2 гербов (в сочетании с одним случаем цифры) равна 3/8, одного герба и 2 цифр – 3/8, ни одного герба – 1/8. При 3 независимых событиях степень бинома равна 3.
Вероятности отдельных возможных исходов даются последовательными членами разложения:
(р + q)3 = p3 + 3p2q + 3pq2 + q3.
При p = q = 1/2 имеем (1/2 + 1/2)3 = 1/8 + 3/8 + 3/8 + 1/8, т. e. то же, что и непосредственным подсчетом.
Если число независимых случайных событий n, то вероятность n, n–1, n–2 и т. д. благоприятных исходов равна последовательным членам разложения:
(р + q)n
Если желаем получить вероятные численности разных исходов при данном числе испытаний n, применяем выражение:
N × (p+q)n
Например, при числе испытаний N = 200 и двух независимых событиях n в каждом испытании вероятные численности будут равны 200×(p+q)2 = 200×(р2+2р×q+q2). Если p = q = 1/2, имеем последовательные вероятные численности: 50 + 100 + 50.
При подбрасывании монеты 200 раз (N = 200) выпадения герба следует ожидать в 50 случаях, герба или цифры – в 100 случаях и цифры – 50 случаях.
При тех же р и N, но n = 3 получим последовательные вероятные численности: 25 + 75 + 75 + 25, которые означают 3, 2, 1 наступление события и ненаступление его, причем сумма всех численностей равна N.
При 200 бросаниях трех монет ожидаем в 25 случаях выпадения 3 гербов (ТТТ), в 75 случаях выпадения 2 гербов и одной цифры (ТТН), в 75 случаях выпадения 2 цифр и одного герба (ННТ) и в 25 случаях – 3 цифр.
Итак, когда вероятности независимых событий известны априори, то можно определить вероятные численности любого данного числа n, n–1, n–2.... наступления события и ненаступления его. При этом неважно, равны или не равны р и q, лишь бы они оставались при испытаниях постоянными. Этот факт имеет большое значение в теории статистики.
При изучении природных явлений выделение элементарных событий и вообще расчленения причинного процесса, в результате которого происходят случайные события, обычно невозможно. Классический подход к определению вероятности здесь бессилен. Проблему определения вероятностей таких событий решают на основе статистического подхода.
Однако классический подход к определению вероятностей событий лежит в основе теории анализа случайных событий и теоретических (модельных) распределений исходов испытаний. В свою очередь теория математического анализа случайных событий и модели распределений исходов испытаний являются базой статистических методов, в частности, базой статистических заключений.
Альтернативные, дискретно варьирующие признаки, как было показано выше, распределяются так, что вероятные численности их появления могут быть найдены по формуле бинома Ньютона:
 (3.1)
(3.1)
где n – число независимых исходов в одном испытании; р – вероятность благоприятного исхода одного случая; q – вероятность неблагоприятного исхода; N – общее число испытаний (исходов).
При n = 6 возможны 26 = 64 исходов. При равной вероятности альтернатив, т. е. при условии р = q = 0,5, получим следующий ряд вероятных численностей:
64(0,5 + 0,5)6 = 64 [1/64 + 6/64 + 15/64 + 20/64 + 15/64 + 6/64 + 1/64] = 1+6+15 + 20 + 15 + 6+1
Откладывая значения числа наступления благоприятных исходов m по оси абсцисс, а значения вероятных численностей – по оси ординат, получим многоугольник численностей распределения (рисунок 3.1). Ломаная линия, соединяющая точки на графике, называется кривой распределения.
Найденные по формуле бинома численности или биномиальные коэффициенты (при p = q = 0,5) можно получить также при помощи треугольника Паскаля (таблица 3.1). Числовые значения коэффициентов построены так, что любой из них получается суммированием двух стоящих над ним строкой выше значений, справа и слева.
Значения коэффициентов, начиная с единицы, закономерно возрастают до определенного уровня, а затем в той же последовательности уменьшаются. Кривые, изображающие биномиальные распределения с р = q = 0,5, симметричны. При любой степени бинома п число коэффициентов равно n+1, например при
n = 1 оно равно 2 и т. д. Сумма биномиальных коэффициентов равна 2n, как в нашем примере, n = 6; N = 26 = 64.
Если р и q не равны, распределение будет асимметрично, причем тем в большей степени, чем меньше n. При большом n, например 30 и более, оно симметрично и малоступенчато. Характер распределения остается тем же, независимо от того, выражено оно в значениях вероятности или в значениях частоты m ожидаемого события.

Рисунок 3. 1 – Кривая распределения
Таблица 3.1 – Треугольник Паскаля
| n | Биномиальные коэффициенты | N=2n | ||||||||||
Для вычисления вероятностей у события (появиться m раз в n независимых испытаний) наряду с формулой бинома применяют также формулу Якоба Бернулли:
 (3.2)
(3.2)
Здесь  – число сочетаний из n элементов по m, или биномиальный коэффициент;
– число сочетаний из n элементов по m, или биномиальный коэффициент;
р – вероятность ожидаемого события (благоприятного исхода);
q = 1 – р – вероятность противоположного события; m – частота появления ожидаемого события; n –число испытаний; n! и m! –факториалы, т. е.: 1×2×3×...× n и 1×2×3×...× m.
Совокупность вероятностей при m = 1, 2, 3,...n называется биномиальным распределением вероятностей.
Так, для предыдущего примера, при p = q = 0,5, n = 6 и
m = 0, 1, 2,..., 6 вероятности будут:
m = 0 
m = 1 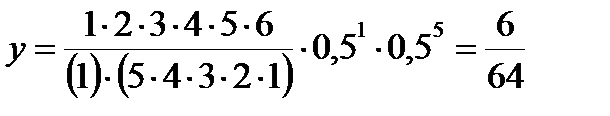
m = 2 
при m = 3, 4, 5, 6 вероятности соответственно будут равны:
20/64; 15/64; 6/64; 6/64 т. е. такие, какие получены по формуле бинома.
Биномиальное распределение определяется двумя параметрами: средней величиной μ = np и дисперсией  или квадратическим отклонением
или квадратическим отклонением  .
.
Для рассматриваемого примера имеем среднюю частоту ожидаемого случайного события m = nр = 6 – 0,5 = 3 и дисперсию
s2 = npq = 6 × 0,5 × 0,5 = 1,5.






