1) одну инерциальную СО от другогй
2) инерциальную СО, находящуюся в гравитационном поле от другой инерциальной СО, в которой поле отсутствует
3) неинерциальную СО от инерциальной, находящейся в гравитационном поле.
4) одну неинерциальную СО от другой, движущейся с другим ускорением.
Принцип эквивалентности масс провозглашает эквивалентность
1) массы покоя и релятивистской массы;
2) массы, движущейся по инерции, и массы, движущейся с ускорением
3) массы у поверхности Земли и массы поднятой над Землей на некоторую высоту
4) гравитационной массы и инерционной массы.
22. Первая космическая скорость – это скорость,
1) которую достигла первая, запущенная в СССР ракета;
2) которую сообщает спутнику первая ступень ракеты;
3) которая позволяет спутнику выйти на околоземную орбиту;
4) которая позволяет осуществить межпланетные перелеты.
23. Вторая космическая скорость – это скорость,
1) которую сообщает космическому кораблю вторая ступень
ракеты;
2) которая позволяет ракете выйти из сферы земного притяжения;
3) необходимая для межзвездных путешествий (субсветовая
скорость)
4) спутника на орбите.
Колебания и волны.
1. На пружине подвешен груз, масса которого 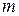 . Если к грузу прикрепить дополнительно гирьку такой же массы, то собственная частота системы:
. Если к грузу прикрепить дополнительно гирьку такой же массы, то собственная частота системы:
1) увеличится в 2 раза;
2) увеличится в  раз;
раз;
3) уменьшится в  раз;
раз;
4) уменьшиться в 2 раза.
2. Тело, масса которого  колеблется под действием силы
колеблется под действием силы  (
(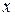 в см,
в см, 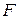 в Ньютонах ). Собственная циклическая частота системы равна:
в Ньютонах ). Собственная циклическая частота системы равна:
1) 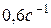 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
3. При увеличении амплитуды колебаний груза на пружине в 2 раза, период колебаний:
1) уменьшиться в 2раза;
2) уменьшиться в  раз;
раз;
3) не изменится;
4) увеличиться в  раз.
раз.
4. Собственные колебания механической системы будут гармоническими, если возвращающая сила:
1) постоянна;
2) пропорциональна смещению из положения равновесия;
3) пропорциональна квадрату смещения
4) пропорциональна косинусу (или синусу) смещения.
5. Колебания происходят по гармоническому закону, если потенциальная энергия колеблющегося тела U зависит от смещения x из положения равновесия следующим образом:
1)  ; 2)
; 2)  ; 3)
; 3) 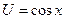 ; 4)
; 4)  .
.
6. Фаза колебаний измеряется: 
1) в метрах;
2) в секундах;
3) в радианах;
4) в герцах.
7. Период малых колебаний математического маятника равен:
1)  ; 2)
; 2) 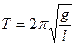 ; 3)
; 3)  ; 4)
; 4)  .
.
8. Период малых колебаний физического маятника, имеющего массу m и момент инерции относительно оси вращения J ( - расстояние от оси до центра масс) равен:
- расстояние от оси до центра масс) равен:
1)  ; 2)
; 2)  ;
;  ;
; 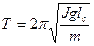 .
.
9. Собственная частота ω0 малых колебаний математического маятника, имеющего массу m, длину l ( g - ускорение свободного падения) равна:
1)  ; 2)
; 2) 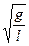 ; 3)
; 3)  ; 4)
; 4)  .
.
10. Собственная частота ω0 малых колебаний физического маятника имеющего массу m , момент инерции J, у которого расстояние от оси до центра массы  , равна:
, равна:
1)  ; 2)
; 2) 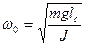 ; 3)
; 3)  ; 4)
; 4)  .
.
11. Если частота звучания двух струн отличается на 16 Гц, то период изменения громкости их совместного звучания будет равен:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 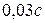 .
.
12. Период малых колебаний математического маятника равен  . Если его поместить в лифт, опускающийся с ускорением (направленным вниз)
. Если его поместить в лифт, опускающийся с ускорением (направленным вниз)  , то колебания будут происходить с частотой:
, то колебания будут происходить с частотой:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
13. Период малых колебаний математического маятника равен  . Если маятник поднимают вверх с ускорением
. Если маятник поднимают вверх с ускорением  , то его колебания будут происходить с частотой:
, то его колебания будут происходить с частотой:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
14. При сложении двух колебаний с одинаковыми частотами, начальные фазы которых 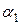 и
и  амплитуда результирующего колебания а связана с амплитудами каждого из колебаний (
амплитуда результирующего колебания а связана с амплитудами каждого из колебаний ( и
и  ) соотношением:
) соотношением:
1) 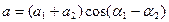 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
15. Если периодический процесс имеет негармонический характер, то его можно представить:
1) как сумму гармонических колебаний с кратными частотами;
2) как сумму гармонических колебаний с близкими частотами;
3) как сумму колебаний с одной частотой, имеющих различные начальные фазы;
16. Биения возникают:
А) при сложении колебаний с близкими частотами;
В) при сложении колебаний с кратными частотами.
Биения представляют собой:
С) короткие импульсы колебаний, перемежающиеся паузами без колебаний,
D) гармонические колебания с периодически меняющейся амплитудой.
Правильными являются утверждения:
1) АС; 2) АD; 3)ВС; 4) BD.
17. При сложении взаимно перпендикулярных гармонических колебаний с одинаковой частой траектория колеблющегося тела может быть:
А) прямой,
В) параболой,
С) синусоидой,
D) эллипсом.
Справедливы утверждения:
1) АВ; 2) ВС; 3) СD; 4) DА.
18. Если  -собственная частота колебаний, а
-собственная частота колебаний, а  -коэффициент затухания, то частота затухающих колебаний равна:
-коэффициент затухания, то частота затухающих колебаний равна:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 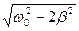 .
.
19. Логарифмическим декрементом затухания называется величина, равная ( А - амплитуда колебаний,  -время затухания,
-время затухания,  -коэффициент затухания, Т- период):
-коэффициент затухания, Т- период):
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
20. Логарифмический декремент затухания  и коэффициент затухания
и коэффициент затухания  связаны между собой соотношением (
связаны между собой соотношением (  -время затухания, Т -период):
-время затухания, Т -период):
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
21. Добротность колеблющейся системы характеризует:
1) насколько механически прочна колеблющаяся система;
2) насколько стабильна частота колебаний;
3) насколько медленно теряется энергия колебаний;
4) насколько процесс колебаний близок к гармоническому.
22. Добротность Q связана с другими характеристиками колебаний ( - коэффициент затухания,
- коэффициент затухания,  - время затухания, Т - период колебаний):
- время затухания, Т - период колебаний):
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
23. Если коэффициент затухания равен 10 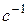 , то амплитуда колебаний уменьшиться в е раз ( е -основание натуральных логарифмов) за время (в секундах):
, то амплитуда колебаний уменьшиться в е раз ( е -основание натуральных логарифмов) за время (в секундах):
1)  ; 2) 0,1; 3) 10; 4)
; 2) 0,1; 3) 10; 4)  .
.
24. Амплитуда затухающих колебаний уменьшается в е раз ( е -основание натуральных логарифмов) за время  , равное (
, равное (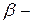 коэффициент затухания,
коэффициент затухания,  логарифмический декремент затухания, Т -период):
логарифмический декремент затухания, Т -период):
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 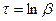 .
.
25. Если  -собственная частота колебаний,
-собственная частота колебаний,  -частота изменения вынуждающей силы,
-частота изменения вынуждающей силы,  -затухание, то вынужденные колебания происходят с частотой:
-затухание, то вынужденные колебания происходят с частотой:
1)  ; 2)
; 2)  ; 3)
; 3) 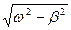 ; 4)
; 4)  .
.
26. Амплитуда вынужденных колебаний равняется ( и
и  - частота вынуждающей силы и собственная частота,
- частота вынуждающей силы и собственная частота,  -коэффициент затухания):
-коэффициент затухания):
1) 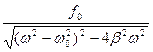 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
27. Если  - собственная частота колебаний, а
- собственная частота колебаний, а  - коэффициент затухания, то резонанс наступит при частоте вынуждающей силы равной:
- коэффициент затухания, то резонанс наступит при частоте вынуждающей силы равной:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 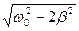 .
.
28. При резонансе амплитуда колебаний достигает величины ( -собственная частота,
-собственная частота,  - частота затухающих колебаний,
- частота затухающих колебаний,  -коэффициент затухания,
-коэффициент затухания,  -приведённая амплитуда вынуждающей силы: 1)
-приведённая амплитуда вынуждающей силы: 1)  ; 2)
; 2)  ; 3)
; 3) 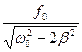 ; 4)
; 4)  .
.
29. Вынужденные колебания сдвинуты по фазе относительно колебаний вынуждающей силы на величину  , определяемую условием:
, определяемую условием:
1)  ; 2)
; 2)  ; 3)
; 3) 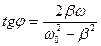 ; 4)
; 4)  .
.
30. При малой величине затухания (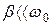 ) в момент резонанса отставание по фазе вынужденных колебаний от обусловившей их вынуждающей силы оказывается близким к величине:
) в момент резонанса отставание по фазе вынужденных колебаний от обусловившей их вынуждающей силы оказывается близким к величине:
1) 0; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
31. Присутствующий в уравнении волны волновой вектор  связан с другими характеристиками волны формулой ( i -обозначает проекция на ось): 1)
связан с другими характеристиками волны формулой ( i -обозначает проекция на ось): 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
32.Скорость распространения упругой волны равна ( , Е,
, Е,  - плотность, модуль Юнга и молярная масса материала в котором распространяется волна):
- плотность, модуль Юнга и молярная масса материала в котором распространяется волна):
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 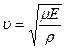 .
.
33.Модуль, присутствующего в уравлении волны вектора  связан с длиной волны λ соотношением ( υ - скорость распространения волны):
связан с длиной волны λ соотношением ( υ - скорость распространения волны):
1)  ; 2)
; 2) 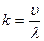 ; 3)
; 3)  ; 4)
; 4) 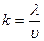 .
.
34. Если волна распространяется по закону  (здесь
(здесь 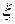 и
и 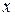 в метрах, а
в метрах, а  в секундах), то длина волны равна:
в секундах), то длина волны равна:
1) 0,4 м; 2) 1 м; 3) 3 м; 4) 6,3 м.
35. Если волна распространяется по закону  (здесь
(здесь 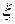 и
и 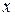 в метрах, а
в метрах, а  в секундах), то скорость волны равна:
в секундах), то скорость волны равна:
1)  ; 2)
; 2)  ; 3)
; 3)  4)
4)  .
.
36. Если распространение волны подчиняется уравнению  (здесь
(здесь 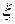 и
и 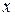 в метрах, а
в метрах, а  в секундах), то частота колебаний (в Герцах) равна:
в секундах), то частота колебаний (в Герцах) равна:
1) 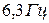 ; 2)
; 2)  , 3)
, 3)  , 4)
, 4) 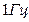 .
.
37. Среднее значение плотности энергии упругой волны равно ( плотность, Е -модуль Юнга среды, а – амплитуда колебаний):
плотность, Е -модуль Юнга среды, а – амплитуда колебаний):
1) 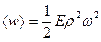 ; 2)
; 2) 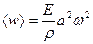 ; 3)
; 3) 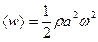 ; 4)
; 4)  .
.
38. Если волновое уравнение имеет вид  , то волна распространяется со скоростью:
, то волна распространяется со скоростью:
1) 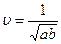 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
39. Если громкость увеличилась на 20 децибел, это означает, что интенсивность звука возросла:
1) в 2раза; 2) в 10 раз; 3) в 20 раз; 4) в 100раз.
40. Если громкость звука увеличилась от 30дБ до 60дБ, то интенсивность звуковой волны возросла:
1) в 2 раза; 2) в 20 раз; 3) в 30 раз; 4) в 1000раз.
41. Эффект Доплера для звука ( - частота источника;
- частота источника; 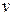 - частота, фиксируемая приемником;
- частота, фиксируемая приемником; 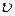 ,
,  ,
,  -скорости звука, источника и приёмника, соответственно)
-скорости звука, источника и приёмника, соответственно)
1)  ; 2)
; 2) 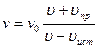 ; 3)
; 3)  ; 4)
; 4)  .
.
Примечание: эффект Доплера записывается для скорости источника и приёмника, двигающихся навстречу друг другу.
42. Высота тонального звука определяется частотой:
1) самой высокочастотной гармоники;
2) самой низкочастотной гармоники;
3) средним значением частот колебаний, образующих звук
4) тональный звук содержит колебания только одной частоты,
она и определяет высоту звука.






