Также как и при описании колебаний, параметрами волны являются амплитуда (ξ0,), циклическая частота (ω), фаза 
и начальная фаза (α), а также, связанные с циклической частотой период и частота (в герцах).
Кроме этого волновой процесс имеет и пространственные характеристики. Во первых, это скорость. Например, когда мы наблюдаем волны на воде, мы следим за гребнем волны, и скорость его движения говорит нам о том, как быстро двигаются волны. Но гребень - это точки, находящиеся в фазе максимального отклонения. То есть мы следим, за тем, как перемещается максимальная фаза колебаний. Но можно следить и за скоростью движения «провалов» или какой-то другой фазы. Во всех этих случаях мы получим величины, характеризующую скорость распространения волны. Поэтому под скоростью волны мы понимаем скорость движения волновой поверхности, имеющей определенную фазу. Эта скорость называется фазовой скоростью волны. Термин фазовая часто опускается, по крайней мере до тех пор, пока не возникает необходимость сравнить эту скорость с групповой скоростью волн.
Расстояние между двумя соседними волновыми поверхностями, имеющими одинаковую фазу (например, расстояние между гребнями волн на воде) называется длиной волны и чаще всего обозначается буквой λ (лямбда). Поскольку фаза повторяется через интервалы времени, равные периоду Т, длина волны равняется расстоянию пройденному волной за это время:
.
Длина волны связана с волновым числом k. Учитывая, что 
, получим:
.
Волновое уравнение.
Уравнение волны 
это функция времени t и координат x,y,z, входящих в радиус-вектор 
.
Эта функция является решением дифференциального уравнения второго порядка. В более простом одномерном случае уравнение имеет вид:
.
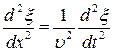Это дифференциальное уравнение содержит производные по времени и по координате. Важно отметить, что коэффициент, связывающий временну́ю часть с координатной равен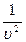 
, где υ - скорость волнового процесса, описываемого решением данного уравнения. Это означает, что правильно составив уравнение, мы сразу получим информацию о скорости волны.
Если при решении конкретной задачи нам необходимо при составлении уравнения учитывать все три координаты, волновое уравнение будет иметь вид:
,
где
- дифференциальный оператор, предполагающий взятие вторых производных по всем трем координатам. И в этом варианте волнового уравнения скорость распространения волны входит в коэффициент, связывающий производную по времени с производными по координатам.
Волны в упругой среде.
Для того чтобы в упругой среде возникли колебания нужно сместить частицы среды из положения равновесия. Сила упругости будет стремиться вернуть эти частицы в положение равновесия, увлекая при этом в процесс колебаний соседние области упругой среды – пойдет волна. Такая упругая волна будет, например, распространяться в стальном рельсе после улара молотком по его торцу - рельс начинает гудеть.
Чтобы проанализировать этот процесс надо рассмотреть движение
очень маленького объема, имеющего массу Δm под действием сил упругости: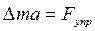 
.
Δm выражается через объем 
, с использованием плотности материала 
.
Ускорение это вторая производная по времени смещения из положения равновесия: 
.
Для нахождения силы необходимо учесть разницу внутреннего напряжения на двух торцах выделенного объема. Внутреннее напряжение оценивается по величине деформации 
с использованием модуля Юнга Е. В результате, сила оказывается равной 
. Таким образом, использование второго закона Ньютона в итоге приводит к равенству:
.
Или после сокращения:
.
Видно, что получено волновое уравнение, решением которого будет уравнение, описывающее волновой процесс в упругой среде. Коэффициент перед второй производной по времени говорит, что эта волна будет распространяться со скоростью
.
Данный результат получен для продольной волны. Но в упругой среде может распространяться и поперечная волна. В этом случае вместо модуля Юнга должен быть учтен модуль сдвига G, и, соответственно скорость распространения волны будет равна:
.
В газовой среде может распространяться только продольная волна, и величина ее скорости зависит от параметров состояния газа: температуры T, давления p, молярной массы μ, показателя адиабаты γ и универсальной газовой постоянной R:
.
Энергия упругой волны
Энергия волны также как энергия колебаний складывается из кинетической и потенциальной энергии. Поскольку буква Е сейчас занята обозначением модуля Юнга привлечем для обозначения энергии латинскую букву W. Итак,
.
Кинетическая энергия выражается через скорость. Скорость колеблющихся частиц это производная по времени смещения из положения равновесия ξ:
.
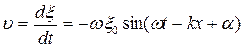Поэтому кинетическая энергия элементарного объема ΔV равняется
.
Потенциальная энергия связана с упругой деформацией
.
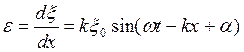И в том же объеме ΔV ее величина равна
.
Для получения плотности w энергии волны просуммируем кинетическую и потенциальную энергию и разделим на ΔV. Кроме того учтем, что 
.
Этот результат говорит о том, что плотность энергии каждый момент времени в разных точках пространства различна. При нахождении среднего по времени значения плотности энергии в каждой точке среды усреднение квадрата синуса дает коэффициент ½:
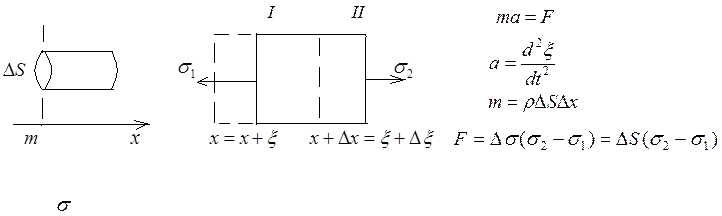С одной стороны волна это процесс, связанный с движением в пространстве, с другой стороны этому процессу соответствует определенный запас энергии. Следовательно, мы можем говорить о переносе волной энергии. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии. Плотность потока энергии это количество энергии, переносимое через единичную площадку за единицу времени. Величина эта равна произведению плотности энергии волны на скорость ее распространения.
.
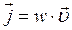Этот вектор плотности потока энергии называется вектором Умова.
Когда говорят об интенсивности волны, то имеют ввиду среднее значение плотности потока энергии, переносимой волной:
Как видно из полученного выражения, интенсивность волны пропорциональна квадрату частоты и квадрату амплитуды.
