1. Момент импульса это:
1) 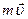 , 2)
, 2) 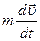 , 3)
, 3) 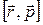 , 4)
, 4)  .
.
2. Вектор момента импульса 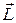 :
:
1) параллелен вектору импульса  ;
;
2) параллелен радиусу-вектору 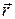 ;
;
3) перпендикулярен вектору  ;
;
4) перпендикулярен произведению 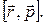
3. Если 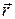 - радиус – вектор,
- радиус – вектор,  - импульс,
- импульс, 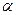 - угол между
- угол между 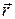 и
и  , то модуль момента импульса
, то модуль момента импульса 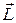 равен:
равен:
1)  , 2)
, 2)  , 3)
, 3) 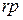 , 4)
, 4) 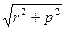 .
.
4. Момент импульса равен:
1) проекции импульса на направление радиус-вектора;
2) мгновенное значение изменения импульса;
3)векторному произведению радиус-вектора на импульс;
4) скалярному произведению радиус-вектора на импульс.
5. Летящая горизонтально пуля ударяется в центр мишени, закреплённой на вертикальном щите. Скорость пули 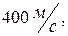 масса
масса 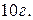 расстояние от центра мишени до основания щита 3м. Момент импульса пули относительно основания щита, когда она находилась на расстоянии 4м от мишени равен:
расстояние от центра мишени до основания щита 3м. Момент импульса пули относительно основания щита, когда она находилась на расстоянии 4м от мишени равен:
1)  , 2)
, 2) 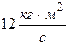 , 3)
, 3) 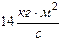 , 4)
, 4) 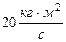 .
.
6. Единицы измерения момента импульса в системе СИ:
1)  , 2)
, 2)  , 3)
, 3) 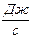 , 4)
, 4) 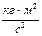 .
.
7. Мяч, брошенный человеком под углом 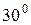 к горизонту, начал полёт на высоте 1,5м. начальная скорость мяча
к горизонту, начал полёт на высоте 1,5м. начальная скорость мяча  , масса 50г. Момент импульса мяча относительно стопы человека, бросившего мяч, в начале полёта равен:
, масса 50г. Момент импульса мяча относительно стопы человека, бросившего мяч, в начале полёта равен:
1)  , 2)
, 2) 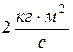 , 3)
, 3) 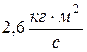 4)
4) 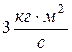 .
.
8. Вектор момента силы  равен:
равен:
1) 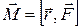 , 2)
, 2)  , 3)
, 3) 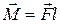 , 4) мгновенному значению силы.
, 4) мгновенному значению силы.
9. Вектор момента силы:
1) параллелен вектору силы;
2) параллелен радиус-вектору;
3) перпендикулярен вектору силы;
4) перпендикулярен векторному произведению 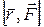 .
.
10. Сторона квадратной пластинки равна 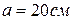 . На один из её углов действует сила
. На один из её углов действует сила 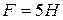 , направленная вдоль одной из сторон пластинки. Момент этой силы относительно противоположного угла пластинки равен:
, направленная вдоль одной из сторон пластинки. Момент этой силы относительно противоположного угла пластинки равен:
1) 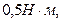 2)
2) 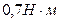 , 3)
, 3) 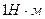 , 4)
, 4) 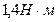 .
.
11. Спутник двигается вокруг Земли по эллиптической орбите. В момент времени, когда он находится на расстоянии 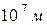 от центра Земли, его скорость составляет угол
от центра Земли, его скорость составляет угол 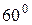 с радиусом орбиты. Если в это время на него действует гравитационная сила
с радиусом орбиты. Если в это время на него действует гравитационная сила  , то момент этой силы относительно центра Земли равен:
, то момент этой силы относительно центра Земли равен:
1) 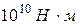 , 2)
, 2) 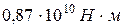 , 3)
, 3)  , 4) 0.
, 4) 0.
12. Тело, масса которого 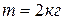 , брошено со скоростью
, брошено со скоростью 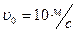 под углом
под углом 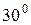 к горизонту. Момент силы тяжести относительно точки бросания через
к горизонту. Момент силы тяжести относительно точки бросания через  равен:
равен:
1)  , 2)
, 2) 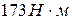 , 3)
, 3) 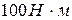 , 4) 0.
, 4) 0.
13. Волчок вращается при наклоне оси относительно вертикали 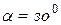 . Расстояние от центра масс волчка до его основания
. Расстояние от центра масс волчка до его основания 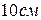 . Масса волчка 500 г. суммарный момент сил, действующих на волчок равен:
. Масса волчка 500 г. суммарный момент сил, действующих на волчок равен:
1) 0, 2) 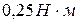 3)
3) 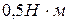 , 4)
, 4) 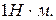
14.Момент импульса 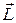 и суммарный момент внешних сил
и суммарный момент внешних сил  связаны между собой соотношением:
связаны между собой соотношением:
1) 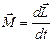 ; 2)
; 2)  ; 3)
; 3) 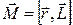 ; 4)
; 4) 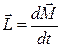 .
.
15. Если на вращающееся тело, имеющее момент импульса 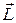 действует сила
действует сила  , создающая момент сил
, создающая момент сил  , то изменение момента импульса
, то изменение момента импульса 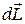 в любом случае направлено:
в любом случае направлено:
1) параллельно 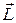 ;
;
2) параллельно  ;
;
3) параллельно  ;
;
4) параллельно векторному произведению  .
.
16. Однородный стержень длиной 1м и массой 4кг вращается вокруг неподвижной оси, проходящей через середину стержня. Если вращающий момент сил равен 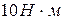 , то угловое ускорение стержня равно:
, то угловое ускорение стержня равно:
1) 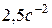 , 2)
, 2) 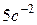 , 3) 7,5
, 3) 7,5 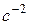 , 4) 30
, 4) 30 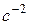 .
.
17. К ободу колеса, имеющего форму диска радиусом 0,2м и массой 10кг, приложена касательная сила 10Н. Угловое ускорение диска равно:
1)  , 2)
, 2)  , 3)
, 3) 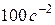 , 4) 1
, 4) 1 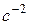 .
.
18. Если на маховик, момент инерции которого 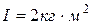 действует момент сил
действует момент сил 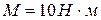 , то маховик вращается с угловым ускорением:
, то маховик вращается с угловым ускорением:
1) 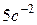 , 2) 10
, 2) 10 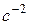 , 3) 20
, 3) 20 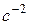 , 4)
, 4)  .
.
19. К ободу маховика диаметром  приложена касательная сила
приложена касательная сила 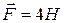 . Если маховик вращается с угловым ускорением
. Если маховик вращается с угловым ускорением  , то его момент инерции равен:
, то его момент инерции равен:
1)  , 2)
, 2) 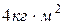 , 3)
, 3) 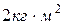 , 4)
, 4) 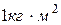 .
.
20..Момент инерции стержня массой m и длиной l , вращающегося вокруг перпендикулярной ему оси, проходящей через один из его концов:
1) 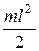 , 2)
, 2) 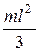 , 3)
, 3)  , 4)
, 4) 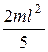 .
.
21. Момент инерции диска относительно перпендикулярной ему оси, проходящей через его край ( m – масса, R – радиус диска):
1) 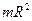 , 2)
, 2) 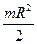 , 3)
, 3)  , 4)
, 4) 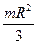 .
.
22. Если масса цилиндра 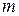 , а радиус
, а радиус 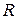 , то его момент инерции относительно оси равен:
, то его момент инерции относительно оси равен:
1)  , 2)
, 2) 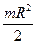 , 3)
, 3) 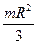 , 4)
, 4) 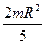 .
.
23.Найти момент инерции твёрдого тела J, имеющего объём 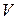 относительно его центра масс, можно по формуле (
относительно его центра масс, можно по формуле (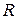 - расстояние до оси вращения,
- расстояние до оси вращения, 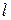 - максимальный размер):
- максимальный размер):
1)  ; 2)
; 2) 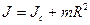 ; 3)
; 3) 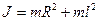 ; 4)
; 4)  .
.
24.По теореме Штейнера момент инерции тела массой 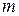 и радиуса R относительно произвольной оси, находящейся на расстоянии
и радиуса R относительно произвольной оси, находящейся на расстоянии  от центра масс «с» равен:
от центра масс «с» равен:
1)  , 2)
, 2) 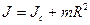 , 3)
, 3) 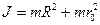 , 4)
, 4)  .
.
25.При вращении твёрдого тела вокруг неподвижной оси  , под действием силы
, под действием силы 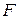 , имеющий момент
, имеющий момент  , угловое ускорение
, угловое ускорение  может быть найдено по формуле ( J - момент инерции):
может быть найдено по формуле ( J - момент инерции):
1) 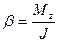 , 2)
, 2) 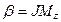 , 3)
, 3) 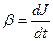 , 4)
, 4) 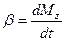 .
.
26. Проекция момента импульса на неподвижную ось  твёрдого тела, вращающегося с угловой скоростью
твёрдого тела, вращающегося с угловой скоростью  равна:
равна:
1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 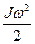 .
.
27. Момент инерции однородного цилиндра диаметром 20 см, массой 10 кг равен:
1)  , 2)
, 2)  , 3)
, 3) 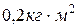 , 4)
, 4) 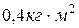 .
.
28. Момент инерции шара диаметром 10 см и массой 10 кг равен:
1) 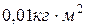 , 2)
, 2) 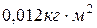 , 3)
, 3)  , 4)
, 4)  .
.
29. При вращении вокруг неподвижной оси  уравнение динамики принимает вид (J – момент инерции, М - момент сил,
уравнение динамики принимает вид (J – момент инерции, М - момент сил,  - угловая скорость):
- угловая скорость):
1) 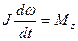 , 2)
, 2) 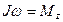 , 3)
, 3) 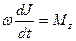 , 4)
, 4) 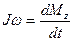 .
.
30. Если  это равнодействующая всех сил, приложенных к центру масс тела, а
это равнодействующая всех сил, приложенных к центру масс тела, а 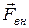 - равнодействующая только внешних (по отношению к движущемуся телу) сил, то для скорости центра масс выполняется соотношение:
- равнодействующая только внешних (по отношению к движущемуся телу) сил, то для скорости центра масс выполняется соотношение:
1) 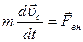 , 2)
, 2) 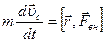 , 3)
, 3)  , 4)
, 4)  .
.
31. В центральном симметричном поле сила 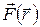 подчиняется условию (
подчиняется условию (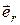 - единичный вектор, совпадающий по направлению с
- единичный вектор, совпадающий по направлению с 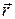 )
)
1) 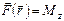 , 2)
, 2)  , 3)
, 3) 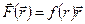 , 4)
, 4)  .
.
32. В центрально симметричном поле сохраняется:
1) только механическая энергия;
2) механическая энергия и импульс;
3) механическая энергия и момент импульса;
4) момент импульса и импульс.
33. Момент инерции материальной точки J имеющей массу 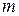 равняется (
равняется ( -радиус – вектор,
-радиус – вектор, 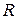 - расстояние от материальной точки до оси вращения,
- расстояние от материальной точки до оси вращения, 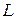 - момент импульса):
- момент импульса):
1)  , 2)
, 2)  , 3)
, 3) 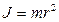 , 4)
, 4) 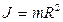 .
.
34.По горизонтальной поверхности катится цилиндр, вращаясь с угловой скоростью  . Радиус цилиндра
. Радиус цилиндра 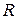 , масса
, масса 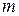 . Кинетическая энергия цилиндра в данном случае равна:
. Кинетическая энергия цилиндра в данном случае равна:
1) 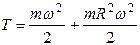 , 2)
, 2)  ,
,
3)  , 4)
, 4) 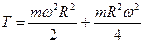 .
.
3 5. Кинетическая энергия при плоском движении твёрдого тела (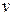 - скорость поступательного движения,
- скорость поступательного движения, 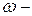 угловая скорость вращения) равна:
угловая скорость вращения) равна:
1)  , 2)
, 2) 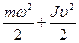 , 3)
, 3) 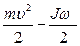 , 4)
, 4) 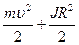 .
.
36. При вращении маховика, радиус которого 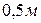 , точка на его ободе двигается со скоростью
, точка на его ободе двигается со скоростью 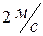 . Если момент инерции маховика
. Если момент инерции маховика  , то его кинетическая энергия равна:
, то его кинетическая энергия равна:
1) 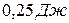 , 2)
, 2) 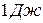 , 3) 4
, 3) 4  , 4)
, 4) 
37. Кинетическая энергия при вращении вокруг неподвижной оси равна:
1)  , 2)
, 2)  , 3)
, 3) 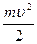 , 4)
, 4) 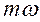 .
.
38. Стержень длиной  и массой
и массой 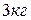 вращается вокруг одного из своих концов с угловой скоростью
вращается вокруг одного из своих концов с угловой скоростью 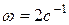 . Его кинетическая энергия равна:
. Его кинетическая энергия равна:
1)  , 2)
, 2) 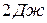 , 3)
, 3) 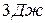 , 4)
, 4) 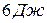 .
.
39. Работа силы 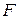 , имеющей момент
, имеющей момент  , при повороте на угол φ вокруг неподвижной оси при прохождении материальной точки пути s равна:
, при повороте на угол φ вокруг неподвижной оси при прохождении материальной точки пути s равна:
1) 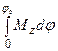 , 2)
, 2) 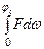 , 3)
, 3) 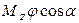 , 4)
, 4) 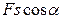 .
.
40. Если с горки высотой h скатываются труба и сплошной цилиндр, имеющие одинаковые массу и радиус, то у подножия горки:
1) их скорости будут одинаковы;
2) скорость цилиндра будет больше;
3) скорость трубы будет больше;
4) скорость будет больше у объекта, имеющего меньшую длину.
41. Колесо в виде обода скатывается с горки высотой 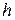 . Скорости колеса в начале υ1 и в конце υ2 связаны между собой:
. Скорости колеса в начале υ1 и в конце υ2 связаны между собой:
1)  , 2)
, 2) 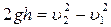 , 3)
, 3) 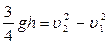 , 4)
, 4) 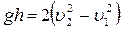 .
.
Горизонтальный стержень может вращаться вокруг вертикальной оси, проходящей через его центр. Масса стержня, длина -. В конец стержня попадает пуля, летевшая со скоростьюυи застревает в нём (масса пули). Стержень начинает вращаться. Как скорость конца стержня связана со скоростью пули?
1)  , 2)
, 2) 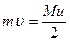 , 3)
, 3) 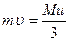 , 4)
, 4)  .
.
43. Если на вращающейся платформе человек переходит с одного места на другое, то изменение угловой скорости от 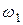 до
до 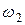 подчиняется следующему соотношению (
подчиняется следующему соотношению (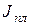 - момент инерции платформы,
- момент инерции платформы,  и
и 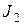 моменты инерции человека в начальном и конечном положениях)
моменты инерции человека в начальном и конечном положениях)
1) 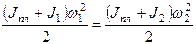 , 2)
, 2) 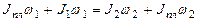 ,
,
3)  , 4)
, 4) 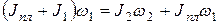 .
.
44. Диск массой 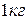 и диаметром
и диаметром 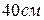 вращается с угловой скоростью 20 с-1 вокруг оси, проходящей через его центр, перпендикулярно плоскости диска. Для того, чтобы его остановить, надо совершить работу:
вращается с угловой скоростью 20 с-1 вокруг оси, проходящей через его центр, перпендикулярно плоскости диска. Для того, чтобы его остановить, надо совершить работу:
1) 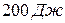 , 2)
, 2) 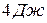 , 3)
, 3) 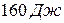 , 4)
, 4) 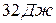 .
.






