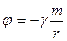Ньютон сделал вывод, что природа силы, «заставляющей падать на землю яблоко» и силы, заставляющая вращаться вокруг Земли Луну, одинакова и это сила гравитационного взаимодействия тел:
.
Здесь m 1 и m 2 - массы притягивающих друг друга тел, r 12- расстояние между ними. А γ – гравитационная постоянная:
γ = 6,67·10-11Н м2/кг2.
Этот закон получил название закон всемирного тяготения, поскольку объединяет явления «земные» и «небесные». Приведенная выше запись закона всемирного тяготения дает информацию о величине (модуле) силы. При анализе явлений, связанных с законом всемирного тяготения возникает необходимость записывать и использовать вектор силы. Для этого чаще всего достаточно мысленно совместить начало координат с одним из тел m 1. Тогда вектор силы F 21, действующий на второе тело m1 со стороны первого, может быть записан в виде:
;
здесь 
- единичный вектор, совпадающий по направлению с радиус- вектором 
, проведенным от первого тела ко второму: 
.
Строго говоря, приведенные выше формулы, применимы только для точечных масс. То есть для случая, когда, размеры взаимодействующих тел значительно меньше расстояния между ними. Если это ус
ловие не выполняется, то в общем случае
для решения задачи о взаимодействии двух
тел необходимо мысленно разбить каждое
тело на элементарные (очень маленькие) массы
m и ml. И записать силу взаимодействия
Рис.24. К взаимодействию между двумя элементарными массами как
«габаритных» тел.. для точечных масс. А затем сложить все силы,
для чего применить операцию двойного суммирования:
.
Тем не менее можно показать, что в случае, когда большое по размеру шарообразное тело массой М взаимодействует с телом, которое можно считать материальной точкой (m), взаимодействие их подчиняется такой же формуле, что и взаимодействие точечных масс:
Гравитационное поле и его характеристики
Гравитационное взаимодействие осуществляется посредством гравитационного поля. Это означает, что любое тело, имеющее массу m , создает гравитационное поле, а другое тело m′ испытывает воздействие со стороны поля. В связи с этим задачу о гравитационном взаимодействии можно разделить на два этапа. Сначала найти характеристики этого поля, а затем, используя их определять результаты воздействия поля на тело, оказавшееся в этом поле. Таких характеристик две: напряженность и потенциал.
Напряженность гравитационного поля - это силовая характеристика поля, физический смысл которой - сила, действующая на единичную массу:
.
По размерности напряженность гравитационного поля совпадает с ускорением. И в частном случае у поверхности Земли, то есть, когда 
а 
модуль напряженности гравитационного поля равен:
Эта величина равняется ускорению свободного падения: 
(g =9,8 м/c2/).
Если сосчитать работу гравитационных сил, то окажется, что эта работа не зависит от формы и длины пути:
.
Это означает, что гравитационное поле имеет градиентный характер и с ним можно сопоставить потенциальную энергию. Поскольку в градиентном поле работа равна разности потенциальных энергий:
,
То можно сделать вывод, что потенциальная энергия тела масса которого m′ в гравитационном поле тела, имеющего массу m, равна:
.
Данная формула предполагает нулевой уровень потенциальной энергии на бесконечности.
Для того, чтобы ввести энергетическую характеристику поля необходимо также привести энергию к единичной массе. Эта величина называется потенциалом гравитационного поля:
.
В частности потенциал поля, которое создается массой m (если эту массу можно считать точечной), равен:
