Гироскопический эффект. Прецессия

Гироскоп – массивное тело, имеющее ось симметрии, которое вращается вокруг этой оси с очень большой угловой скоростью. Какую скорость мы можем считать «очень большой»? Это требование важно для случая, когда гироскоп участвует в дополнительном вращательном движении с угловой скоростью . Тогда, при выполнении условия , можно считать, что направление момента импульса совпадает с осью вращения гироскопа:

.

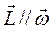
Рис. 18 Гироскопический эффект Если на гироскоп подействовать силой

(на чертеже она направлена от нас), то возникающий момент сил направлен перпендикулярно этой силе (см. рис). Согласно уравнению моментов:

вектор изменения момента импульса совпадает по направлению с вектором момента силы. А это значит, что ось гироскопа будет стремиться повернуться в направлении перпендикулярном приложенной силе. То есть в приведенном примере мы действуем на гироскоп от нас, а он наклоняется в сторону - влево. Это одно из проявлений гироскопического эффекта.

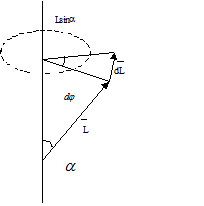
Если сила, стремящаяся повернуть ось гироскопа, действует постоянно, то может возникнуть прецессия гироскопа. Рассмотрим в качестве примера волчок (гироскоп), ось которого наклонена. Тогда сила тяжести mg и реакция опоры N создают пару сил, стремящуюся опрокинуть волчок. Но момент этих сил направлен перпендикулярно оси волчка и так же направлен вектор изменения импульса. В этой ситуации ось волчка будет вращаться вокруг вертикали, проведенной из точки опоры волчка (см. рисунок).

Для того, чтобы определить частоту прецессии рассмотрим эту ситуа-

цию более подробно. Момент сил пары сил можно считать относительно

любой точки. Относительно точки опоры волчка момент сил будет равен 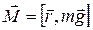, модуль его соответственно 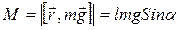, где α – угол между радиус-вектором (направленным вдоль оси волчка) и силой тяжести.

 

:

 

Рис 19. Прецессия гироскопа

 

С другой стороны, если за время dt ось волчка повернется на dφ, то модуль изменения вектора момента импульса будет равен (см. рисунок) . Подставив эти результаты в уравнение моментов, приняв во внимание при этом, что , получим: 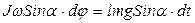. Отсюда следует, что частота прецессии 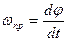равна:

.

Чем меньше частота вращения волчка-гироскопа, тем больше частота прецессии.

 

 

Глава 4. Неинерциальные системы отсчета и гравитационное поле.

 

Силы инерции

Рассмотрим две системы отсчета:

инерциальную (ИСО) и неинерци-

альную (НеИСО). - ускорение

НеИСО, направленное вдоль оси х.

При t=0 системы совпадают. Через

некоторое время t 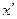уйдет от х

на расстояние . И тогда

Рис. 20. ИСО и НеИСО

 

По второму закону Ньютона в ИСО: . Используя преобразование координаты x, получим:

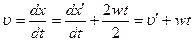и

Таким образом, мы видим, что при переходе из ИСО в НеИСО второй закон Ньютона изменяет свой вид:

для ИСО:

для НеИСО: .

Но если записать второй закон Ньютона в форме

,

появляется возможность записывать его в НеИСО так же как в ИСО. Но для этого надо считать второе слагаемое справа некоей дополнительной силой. Эта сила называется силой инерции:

.

Поскольку сила инерции не связана ни с каким из выше перечисленных взаимодействий, она является некоей условной силой - псевдосилой. Благодаря введению понятиясилы инерции, оказалось возможным записывать второй закон Ньютона в НеИСО так же, как и в ИСО:

;

Но при этом надо учитывать, что под понимается сумма равнодействующей сил и действующих сил инерции:

 

Центробежная сила.

Центробежную силу надо учитывать во вращающейся НеИСО.

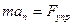Рассмотрим условие равновесия тела массой m во вращающейся НеИСО. На рисунке оно привязана к оси диска вращающегося с частотой ω. С точки зрения наблюдателя, находящегося в ИСО тело вращается вместе с диском, и сила, сообщающая телу нормальное (центростремительное) ускорение – это сила упругости пружинки, которой это тело прикреплено к оси вращения. В ИСО: , где .

В НеИСО тело покоится (относительно диска оно не смещается). Следовательно в

Рис. 21. Центробежная сила этой системе сумма сил, приложенных к

телу (с учетом сил инерции) должна быть равна нулю. В НеИСО: 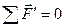, то есть

.

Или:

Отсюда следует, что сила инерции направлено в сторону, противоположную силе упругости, и ее величина зависит от скорости вращения НеИСО. Поскольку эта сила направлено от центра, вокруг которого вращается НеИСО, она называется центробежная сила:

.

 

Сила Кориолиса

Если тело движется во вращающейся НеИСО, возникает эффект, требующий учета еще одной силы инерции – силы Кориолиса. Дело в том, что любое движение во вращающейся НеИСО (кроме движения параллельно ось вращения) приводит к изменению момента импульса движущегося тела. Так, например, если тело двигается в радиальном направлении, у него увеличивается радиус вращения и за счет изменения мо-

мента инерции () согласно формуле

будет увеличиваться и момент импульса.

Следовательно движение тела по прямой вдоль ра-

диуса (см. рис.) может быть осуществлено только,

если какая-то сила создает момент сил, изменяющий

момент импульса. Такой силой может быть реак- Рис. 22 Движение ция «заборчика» поставленного слева от траектории

в НеИСО этого тела. Он будет подталкивать движущееся тело

и увеличивать его момент импульса. Но с точки зрения наблюдателя в НеИСО тело движется по прямой и действие заборчика перпендикулярно траектории должно быть уравновешено другой силой, которая направлена тоже перпендикулярно, но в противоположном направлении. Эта сила и называется силой Кориолиса.

Для того, чтобы определить, чему равняется сила Кориолиса рассмотрим другой случай. Предположим, в НеИСО, вращающейся с угловой

скоростью ω, двигается тело по круговой траектории со скоростью (относительно диска). В ИСО скорость

этого тела будет равна сумме относительной скорости

и скорости вращения вместе с НеИСО:

.

Сила, обеспечивающая такое движение по окружности, должна равняться произведению массы на нормальное (центростремительное) ускорение:

Рис.23. Сила

Кориолиса

 

С точки зрения наблюдателя в НеИСО Тело движется по окружности со скоростью 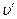и его нормальное ускорение равно . Тогда второй закон Ньютона в НеИСО имеет вид:

.

То есть в этом случае мы должны учитывать две силы инерции (второе и третье слагаемое). Второе слагаемое - это центробежная сила, а третье сила Кориолиса. Совпадение знаков у этих двух слагаемых говорит о том, что в данном случае направления этих сил совпадают.

В общем случае направление силы Кориолиса зависит от направления вращения НеИСО и направления скорости тела, движущегося в этой системе отсчета. Поэтому сила Кориолиса записывается с помощью операции векторного умножения:

.

Соответственно модуль силы Кориолиса равен:

,

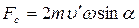где α – угол между векторами и .