1. С разрушением тоталитарных режимов существенно возрос интерес к проблеме разработки адекватного математического аппарата для описания социально - экономических систем (СЭС). К наиболее важным относятся вопросы, связанные с выделением характерных параметров, с использованием которых можно провести классификацию всех возможных состояний СЭС.
В настоящем параграфе описана математическая структура, которая является адекватной для проблемы нахождения и классификации всех возможных состояний СЭС. В качестве примера реализации общего подхода рассмотрен случай простейшей для описания динамики СЭС на макроэкономическом уровне. Изложение ведется на "физическом" уровне строгости, однако восстановление точного "математического" уровня описания не представляет, как правило, затруднений.

|
2. Рассмотрим следующую математическую структуру (Рис.1).
Введем в рассмотрение пространство E всех возможных текущих значений параметров, характеризующих СЭС во всех точках пространства - времени xÎX (город, страна, континент и т.п.). Тогда множество X можно рассматривать как базу, над точками которой при помощи отображения p-1 восстанавливается некий слой FxÌE возможных значений параметров СЭС. Переход к иной точке пространства - времени осуществляется при помощи (группового или полугруппового) преобразования gÎG на точках базы g: x®gxÎX. Слой Fx при таком преобразовании переводится в слой Fgx с помощью отображения Ux(g): Fx®FgxÌE. Заданная конкретная реализация СЭС выделяется некоторой точкой FiÎFx и при преобразованиях gÎG на точках базы задает сечение si(x).
В математическом смысле[87] описанная структура являет собой пример главного расслоения над базой X.
Введем теперь операцию e установления соотношения социально - экономической эквивалентности в пространстве Es всех орбит сечений s(x). Тогда все возможные состояния СЭС могут быть классифицированы при помощи (частично - упорядоченного) множества - "спектра состояний СЭС", которое эквивалентно фактор - множеству S=Ese.
С учетом вышесказанного моделирование социально - экономических явлений можно производить по следующей схеме:
þ Задать пространство E. Его определение должно быть единым (универсальным) и пригодным для широкого класса задач моделирования СЭС.
þ Задать оператор p проектирования на базу X (выбор базы, как правило, диктуется спецификой задачи), с помощью которого выделяется слой Fx над данной точкой базы xÎX (это производится с учетом возможности практического определения необходимых параметров).
þ Задать группу G, которая будет отражать необходимый уровень пространственно - временного рассмотрения.
þ Установить вид отображения Ux(g): Fx®Fgx, где gÎG (в некотором смысле Ux(g) можно назвать оператором "допустимых сценариев").
þ Найти оператор выделения сечений s(x) и построить пространство Es орбит сечений (этот этап по своей сути является чисто математическим и может быть сведен к некоей алгоритмической вычислительной процедуре).
þ Ввести соотношение e эквивалентности орбит в пространстве орбит Es (некоторые предпосылки для выбора соотношения эквивалентности могут быть взяты даже из самой структуры пространства Es).
þ Классификация всех возможных состояний СЭС производится с помощью фактор - множества S=Ese.
В рамках приведенной математической структуры, ориентированной на нахождение спектра состояний СЭС S и на его классификацию однозначный смысл приобретает и термин "процесс" применительно к СЭС, который понимается как переход СЭС от одного состояния к другому.
3. Рассмотрим пример реализации описанной выше процедуры, который можно назвать моделью взаимодействия "связанных" и "свободных" финансов в замкнутой СЭС.
Вначале необходимо рассмотреть те особенности, которые связаны с информационной динамикой в СЭС, ибо только в социальной компоненте может произойти "рождение - синтез" новой информации, важной в экономическом плане.
В финансовом отношении проблема "ценности" информации имеет два измерения. Во-первых, в данное количество информации вложено количество финансов, затраченных на ее получение. Конечно, это количество финансов является различным для разных состояний и структур СЭС. Во-вторых, и это главное, эта синтезированная "экономически - значимая" информация имеет также и независимое финансовое измерение, которое может быть выражено посредством "прибыли" от ее внедрения. Это последнее финансовое измерение также не является инвариантным и зависит от возможностей СЭС по адаптации данной информации и определяется как социальными особенностями (например, наличием специалистов), так и экономическими (например, наличием инфраструктуры, способной перевести эту информацию на технологический уровень, то есть "внедрить" ее).
Таким образом, финансы имеют также и "информационную компоненту, которая сильно связана со спецификой переработки и синтеза информации Человеком, и которая не подчиняется законам сохранения.
В общем случае всю совокупность финансов можно разделить на два основных класса - на "связанные" и "свободные" финансы. Связанные финансы обозначают ту часть финансов, которая вложена в производство новых финансов (например, в технологии, обучение, создание соответствующих инфраструктур и т.п.) и поэтому уже неспособных к движению. Иными словами, связанные финансы уже "овеществлены[88]" и привязаны к неким материальным объектам и структурам. Под свободными финансами понимается та их часть, которая подвижна и может быть переведена в связанное состояние (например, путем вложения их в новые технологии). В свободные финансы входит также и "информационная" компонента, которая синтезирована в СЭС вследствие информационной деятельности Человека[89]. В качестве ее "финансового измерения" можно взять, например, "среднюю прибыль" при внедрении этой информации с учетом данной структуры СЭС (весьма важным является то обстоятельство, что в разных СЭС (например, в разных государствах) финансовое измерение одной и той же новой синтезированной информации будет разным - например, эта величина возрастает при наличии в СЭС инфраструктур, ориентированных на доводку и внедрение информации.
Вследствие вышесказанного связанные финансы Фi и свободные финансы Фc являют собой независимые компоненты финансового поля в макроэкономике: для них, в частности, отсутствует "закон сохранения", то есть Фit + Фct ¹const.
Теперь можно перейти к реализации общей математической структуры для описания макроэкономических процессов в замкнутой СЭС.
В качестве базы естественным образом выбирается время: X=T. На базе T зададим дискретную группу G (дискретную, например, вследствие естественной дискретизации представления социально - экономической статистики), которую можно отождествить с группой целых чисел Z. Так как в главном расслоении производится отождествление базы и группы, то T=Z. В качестве слоя Fx выбираем прямое произведение ФitÄФct. Тогда для нашей модели E=ФiÄФcÄT, а p является оператором проектирования на ось T. Оператор Ux(g), переводящий один слой в другой, для нашей модели будет тождественным, что отвечает неизменным "правилам игры".
Оператор, задающий орбиту сечения по заданному "начальному значению" Фit=0 и Фct=0 в общем виде для замкнутой СЭС записывается так (причем имеют место естественные ограничения Фit>0 и Фct>0)
 (1)
(1)
Учет запрета на неограниченное возрастание значений Фit и Фct, а также учет однородности группы T=Z приводит к распределению знаков для (ai, aс), показанному на Рис. 2 (нетрудно показать, что любой иной простой случай спрямляем к этому типу - см., например, книги в сноске 1). В безразмерных переменных простейший выбор есть
 (2)
(2)

|
Здесь b=Ti/Tc -безразмерный период малых колебаний вблизи точки 1 =(1,1), а Ti и Tc - характерные "времена нарастания" величин соответственно свободных и связанных финансов вблизи точки 1.
Тогда орбиты являют собой винтовые линии в пространстве E, а пространство орбит Es взаимно - однозначно проектируется на плоскость (Фc, Фc) - см. Рис. 2, где оно естественным образом разбивается на прямую сумму пространств
 (3)
(3)
То есть, множество S состоит из двух элементов.
Классификацию орбит можно произвести, например, по их минимальному значению на орбите: Фim=min (Фit)<1 (для нее одновременно Фcm=min (Фct)<1), или же - по их периоду (то есть по минимальному времени Т такому, что Фit+Т=Фit и, соответственно, Фit+Т=Фit).
Итак, в рамках самой простой модели взаимосвязи свободных и связанных финансов для замкнутой СЭС (то есть в отсутствие ее взаимодействия с окружением) могут реализоваться лишь два ее состояния, причем "типичным" является колебательное состояние. Таким образом, хотя данная модель и крайне огрублена, она тем не менее демонстрирует основные черты динамики макроэкономики СЭС, такие как "периодичность" (то есть - "экономические кризисы") и изменение характеристик состояния СЭС (амплитуды, периода колебаний) в результате как внутренней перестройки (когда "сдвигается" точка 1 - см. ниже), так и при внешних воздействиях (когда происходит перевод системы на иную орбиту - см. Рис. 2).
Необходимо также отметить, что учет социальных факторов приводит к выделению орбит с Фim<Фicr<1 (где Фicr - некое критическое значение Фi), которые являются "социально опасными" в том смысле, что оставляют слишком малый резерв запаса свободных финансов для парирования внешних воздействий. Интересно, что данный подход позволяет выделить такие "опасные" орбиты еще далеко в "благоприятной области", когда Фit>>1 и (или) Фсt>>1, что дает время на принятие предупредительных мер.
Данная модель легко обобщается на более сложные зависимости вторых слагаемых в правой части (1). Однако важность этой простой модели состоит в том, что она справедлива всегда для любой замкнутой макроэкономики в "опасной области" - то есть для орбит, далеких от "равновесной точки 1 (см. Рис. 2) и поэтому представляет несомненный практический интерес[90].
4..Перейдем к рассмотрению незамкнутых СЭС.
В общем случае внешнее воздействие на СЭС распадается на два предельных класса: когда t>>Т0 и когда t<<Т0, где t - характерное время внешнего воздействия, а Т0 - период для данной орбиты СЭС.
Рассмотрим случай постоянных внешних воздействий - t>>Т0 (противоположный случай рассмотрен в следующем пункте). Перейдем также к непрерывным координатам, что позволит применять при исследовании методы качественной теории динамических систем на плоскости (см., например[91]).
Итак, уравнения (1) - (2) для открытой СЭС при постоянном внешнем воздействии примут вид
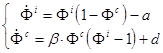 (4)
(4)
Особые точки получаются приравниванием к нулю правой части (4), и для них находим
 (5)
(5)
Здесь обозначено b=db.
Чтобы проследить тенденцию, рассмотрим случай, когда ½a½,½b½<<1. Тогда в первом порядке
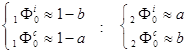 (6)
(6)

Исследование точек 1 и 2 свидетельствует о следующем:
q при a>b точка 1 есть неустойчивый фокус, а 2 - седло; поведение фазовых траекторий (проекций орбит) показано на Рис. 3.

q при a<b точка 1 есть устойчивый фокус, а 2 - седло, см. Рис. 4.
Обратимся к социально - экономической интерпретации полученных данных.
Значения a>0 соответствуют постоянному оттоку свободных финансов из СЭС, что может выражаться, например, в виде так называемой "утечки мозгов" или же вывозу свободного капитала (или же - невывозу капиталов, полученных за экспорт). Значения b>0 соответствуют притоку сторонних связанных финансов - например, товаров или вкладу сторонних капиталов в связанное состояние в данной СЭС.
Таким образом, случай a>0 и b>0 соответствует "экономически слабой" СЭС. Для нее точка 1 сдвигается в сторону меньших средних уровней как свободных, так и связанных финансов по сравнению с замкнутой СЭС[92]. Однако при внешнем воздействии изменяется и устойчивость поведения СЭС: "нейтральный" центр переходит в устойчивый или неустойчивый фокус.
Поведение же СЭС при этом распадается на два сценария.
Первый сценарий реализуется при условии, когда ввоз связанных финансов превышает вывоз свободных, то есть когда внешние капиталовложения в экономику[93] страны и ввоз товаров превышают финансовый эквивалент "утечки мозгов" из страны и вывоз капиталов. Тогда СЭС почти из всех начальных состояний приходит к устойчивому состоянию 1, причем с течением времени "амплитуда кризисов" уменьшается - см. Рис. 4.
К сожалению, чаще реализуется второй сценарий, при противоположном соотношении между величинами вывоза свободных финансов и ввоза связанных финансов, когда почти для всех начальных условий наступает полная деградация и уничтожение СЭС путем полного исчезновения либо связанных, либо свободных финансов (см. Рис. 3). В реальном случае, конечно, при таком сценарии СЭС либо распадается, либо ее распаду помешают такие социальные явления, как диктатуры и войны.
Интересно отметить, что "утечка мозгов" уменьшает средний уровень связанных финансов, что согласуется с "наивной" точкой зрения - "меньше специалистов для внедрения новых технологий". А ввоз чужих капиталов уменьшает средний уровень свободных финансов - ибо "уменьшается выпуск специалистов, способных придумать новые технологии".
Фактически, проанализированный выше случай соответствует внешней экспансии, социально - экономической "атаке" на "слаборазвитую" СЭС. Однако эти же два сценария поведения могут быть реализованы и для "экономически развитых" СЭС, практикующих "ввоз мозгов" и вывоз связанных финансов. В рамках модели (4) этому случаю соответствуют отрицательные значения a и b. Случай превышения притока свободных финансов (например, при "ввозе мозгов") над вывозом связанных финансов стабилизирует "развитые" СЭС (см. Рис. 4). В противном случае СЭС деградирует - и это несмотря на то, что по "внешним признакам" она еще некоторое время может считаться "развитой".
Случай a>0 и b<0 наиболее трагичен - он всегда ведет к деградации СЭС (см. Рис. 3).
Наконец отметим, что для характерного времени "стабилизации" с состоянию 1 (или же - для характерного времени деградации СЭС) может быть получена оценка как Tc~½a-b½-1.
5. Остановимся на некоторых следствиях для посткоммунистических СЭС. Для них характерно, что средний уровень свободных финансов много меньше среднего уровня связанных финансов, или в размерном виде Фi<<Фс. Это является следствием того обстоятельства, что в коммунистических режимах практически полностью отсутствовала инфраструктура для внедрения новой экономически - значимой информации. Поэтому для коммунистического режима a>0 и b<0, а динамика СЭС всегда соответствует Рис. 3. Относительную стабильность таким СЭС мог придать лишь все увеличивающийся вывоз связанных финансов - чаще всего в виде сырья.
Таким образом, главной задачей посткоммунистических СЭС на макроэкономическом уровне является проблема увеличения среднего уровня Фi и уменьшение амплитуды колебаний, то есть сдвиг "вправо" точки 1 (см. рис. 2-4). Осуществить это лишь путем постоянного воздействия со стороны окружающего мира не представляется возможным: как видно из (6), для этого необходимо увеличение вывоза связанных финансов (например, товаров), то есть b<0, что затруднено в силу экономической отсталости страны. Но к тому же при наступлении открытости таких обществ возникает интенсивная "утечка мозгов" (в виде либо физическом, либо информационном), и становится a>0, а тогда деструктивные процессы лишь усиливаются.
Поэтому остается лишь одна возможность: путем перестройки внутренней структуры СЭС, прежде всего в направлении создания инфраструктуры для создания (синтеза) и внедрения новой экономически - значимой информации. Даже внешняя финансовая помощь должна идти не на увеличение доли свободных или связанных финансов (соответственно "без условная" помощь и "целевое финансирование" программ), а лишь на структурную перестройку СЭС. Действительно, "кратковременная" внешняя финансовая поддержка может лишь перевести СЭС на иную орбиту (лучший вариант показан на Рис. 2: переход s3®s2, когда СЭС находится в состоянии А; страна - "донор" при этом должна находиться в состоянии В и осуществить указанный стрелкой переход, чтобы не усугубить свое собственное положение).


Перестройку структуры СЭС можно производить по двум сценариям (Рис. 5 а,б). Либо "быстрым рывком" (Рис. 5а), либо медленным "дрейфом" (Рис. 5б) осуществлять перевод средних уровней 1®11. Первый сценарий соответствует так называемой "шоковой терапии" (и требует существенных кратковременных финансовых вливаний в экономику страны), второй - "китайскому варианту". Отметим при этом, что "шоковый" сценарий требует быстрой структурной перестройки СЭС.
Подробному рассмотрению вопросов перестройки структуры СЭС будет посвящена отдельная работа.
6. Рассмотренная здесь модель макроэкономики СЭС изоморфна известной в популяционной экологии модели "хищник - жертва" для взаимодействующих популяций. Эта модель довольно подробно исследована в математическом плане (см, например[94]), и многие математические выводы сохраняются также и для СЭС.
Аналогия между процессами в социально - экономических и экологических системах имеет ярко выраженный практический интерес: она позволяет производить экспериментальное моделирование макроэкономических процессов посредством интерпретации экологических данных.
7. Подведем основные выводы из приведенного выше:
A) Предложена математическая структура, ориентированная на нахождение спектра всех возможных состояний социально - экономической системы, а также позволяющая корректно определить сам термин "состояние СЭС".
B) Способность Человека производить - синтезировать новую экономически - значимую информацию делает возможным придать ей финансовое выражение, а также разделить всю массу финансов на "связанные" и "свободные", причем информационная компонента включена в последнюю.
C) Простейший вариант взаимодействия связанных и свободных финансов в замкнутой СЭС задается соотношениями (1) - (2) безотносительно к конкретной природе и свойствам этих понятий. В этом смысле такое взаимодействие является универсальным и "единственно возможным".
D) Модели (1) - (2) и (4) корректно описывают основные макроэкономические явления в СЭС, включая проблемы, связанные с устойчивостью СЭС, а также выходом СЭС из посткоммунистического состояния.
E) Важнейшее значение для динамики и устойчивости СЭС имеет наличие и особенности функционирования социально - экономических структур, направленных на появление (синтез) новой экономически - значимой информации и на ее адаптацию и "внедрение" на уровне практики экономической деятельности СЭС. Для посткоммунистических СЭС формирование такой инфраструктуры имеет критическое значение.
8. Наконец, отметим следующее:
þ Трех - и более компонентные модели (например, - несколько отраслей экономики, несколько объектов социально - экономического процесса, несколько партий) с запретом на "инфинитные траектории" могут уже демонстрировать поведение типа так называемого "странного аттрактора", то есть - обладать стохастическим свойствами[95], что резко снижает уровень прогнозируемости развития таких систем.
þ Управление такими системами состоит либо в сохранении, либо в изменении шумовых свойств таких "траекторий" (соответствующих распределений вероятности, размерности аттрактора, корреляционных функций, показателей Ляпунова, f-b - шума и т.п.).
þ Моделирование такого "рынка" - это создание (или изменение существующих) таких аналоговых (например, - электронных) систем, которые проявляют те же самые шумовые свойства.
9. Описанная выше модель имеет значительно более широкую область приложений, чем описание связанных и свободных финансов.
Этой моделью - или ее вариантами - описывается взаимодействие вообще между любыми двумя КС, принадлежащими к одному и тому же уровню иерархии. Действительно: пусть одна КС характеризуется параметром Фi, а другая - параметром Фc. Тогда математическая модель для взаимодействия этих параметров имеет вид (1), а ее простейшая реализация - (1) и (2) (или (3) - при учете взаимодействия этих двух КС с окружающей средой).
Таким образом, моделями (1) - (3) могут быть описаны многие из сторон социальной и экономической активности Человека. В частности, - взаимодействие между двумя партиями или же двумя "общественными мнениями" (и тогда Фi и Фc - это, например, количество людей, придерживающихся соответствующих взглядов или точек зрения) - явление, известное в политологии как "эффект маятника".
Интересно, что наличие в стране 3-х или более "влиятельных" социальных групп (партий, социальных движений и т.п.), как следует из предыдущего пункта, уже не позволяет осуществить надежный политический прогноз и организовать "упорядоченную" передачу власти от одной партии к другой. Вероятно, что это может служить объяснением того, по какой причине в большинстве экономически развитых - и прогнозируемых! - стран мира имеется всего две основные социальные или политические силы ("правящая" и "оппозиционная" группировки), которые периодически сменяют друг друга у власти - по мере того, как они полностью реализуют свою социальную и/или экономическую Программу (или же - по мере того, как будет самой жизнью доказана ее бесперспективность).






