В предыдущем параграфе мы описали математический аппарат, с помощью которого может быть количественно описано распределение по массе финансов для однородных социально - экономических объектов - КС социальной природы. При этом под массой финансов необходимо понимать все имущество данного объекта - как движимое, так и недвижимое, - выраженное в финансовом (денежном) измерении.
Поскольку каждый уровень для социальных иерархических систем состоит из однородных объектов, то такие распределения, построенные для каждого из таких уровней, будут различаться между собой. прежде всего по 1) общей (суммарной) массе финансов, аккумулированной в объектах данного уровня иерархии, 2) средней массе финансов, приходящейся на один единичный структурный элемент данного уровня иерархии - на одну КС, и 3) уровнем вариабельности (изменчивости) массы финансов между отдельными КС. Это - основные параметры, по которым может иметь место такое различие между разными уровнями.
|
В общем случае распределение КС по массе финансов (по общей стоимости их имущества) внутри каждого иерархического уровня будет одномодальным: наличие многомодальности означает наличие нескольких (по числу мод) видов объектов, - что, в общем случае, приводит к нестабильности экономики (см. следующий параграф).
Таким образом, построив график (гистограмму) зависимости N(m) (где N - число объектов (уже произвольного уровня иерархии - от отдельного человека и до транснациональной корпорации), а m - масса финансов, принадлежащих этим объектам), по числу мод данного графика можно найти иерархическое строение данной социальной структуры для социально - экономических иерархических систем произвольной природы - от фирм и до государства (даже - для всей Планеты в целом).
Опишем алгоритм анализа таких графиков.

|
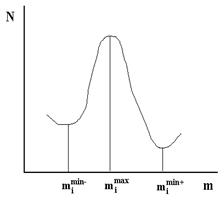
Прежде всего - определим саму степень выраженности иерархии по степени выраженности максимумов распределения N(m). Например, для количественного выражения этой величины можно предложить формулу
 (1)
(1)
Обозначения см. на Рис. 1.
Введенная таким образом величина Pi изменяется от Pi=0 для полного отсутствия иерархического уровня и до Pi=1 для максимально полной отделенности данного иерархического уровня от других.
Далее - из N(m) находим количество иерархических уровней, которые проявляются в функционировании данной социально - экономической структуры. Например, на Рис. 2 изображена трехуровневая иерархическая система.

|
Наконец - область вблизи максимума описываем при помощи блока функций (4) - (5) из предыдущего параграфа (см. Рис. 3), вследствие чего каждый из уровней описывается 3-мя числами. Первое - значение Nimax - наиболее вероятное количество объектов для данного иерархического уровня (количество объектов, которые имеют массу финансов в количестве mimax). Второе - детерминистическое значение массы финансов m0 для объектов данного уровня иерархии (то значение массы финансов, которым обладали бы все объекты в случае, если бы 1) все они были абсолютно одинаковыми и 2) все они находились в абсолютно одинаковых условиях). Третье число - s2, которое описывает уровень вариабельности (разнообразия) либо самих объектов данного уровня иерархии, либо условий, в которых они находятся (более подробно это описано в предыдущем параграфе.)
Интересно также то обстоятельство, что данные экономической статистики позволяют определить уровень развитости также и пирамиды управления в данной стране!
Для такого анализа нужно построить график (гистограмму) N(n), где n - количество людей, работающих в данном объекте - КС, а N - количество объектов с таким количественным составом сотрудников - безотносительно к их уровню иерархии.
Анализ этого графика следует производить совершенно аналогично описанному выше. Спектр чисел {nimax} даст тогда количественный состав пирамиды управления: сравнивая его с представленным в параграфе 2.3, можно сделать заключение о степени оптимальности в организации управления данным объектом, а также выделить наиболее перспективные направления по реконструкции этой пирамиды (распределение {nimax} - а точнее {ni0} - должно приближаться к {16i}, - см. параграф 2.3).
Также совершенно аналогично описанному выше находятся для каждого иерархического уровня свои тройки чисел Nimax, ni0 и sn2, а также - степень Pi(n) выраженности иерархической структуры данного социального объекта (включая и государство в целом). Интересно, что мы можем решать как прямую задачу об оптимальной аппроксимации N(n) - если известен вид зависимости m~ns между массой финансов и количеством сотрудников (для всех уровней иерархии одновременно или же для каждого из уровней в отдельности - соответствующие sобщ или спектр значений {si} могут быть найдены из статистических данных).
Но мы можем решать и обратную задачу: сделав в (4) и (5) замену переменных m®n, мы можем искать те параметры an, bn и sn2, которые наиболее хорошо описывают экспериментальные кривые - а уже после этого, из сравнения найденных значений an, bn, sn2 и am, bm,sm 2 найти зависимость (зависимости) m~ns.
Отметим, что в математическом плане задача о выборе наилучшей аппроксимации заданной кривой с использованием данного класса функций достаточно хорошо разработана и имеется большое количество уже готовых алгоритмов и программ для ее реализации (см., например[86]), и поэтому конкретные методы реализации таких задач здесь мы не описываем.
В заключение этого параграфа сделаем замечание о виде представления экспериментальных (статистических) данных: свести их воедино на одном графике возможно только в дважды логарифмических координатах - то есть когда вдоль осей отложены lgN и lgm (или же lgn; - впрочем, можно использовать и натуральные логарифмы - это не принципиально)






