Условия, по которым должно осуществляться управление, допускают математическую формализацию в рамки стандартной задачи на управление. Ниже кратко опишем эту процедуру (в ряде случаев дополнительная детализация проведена с использованием приближения белого шума для xt и ht - см. Пример).
У1. Одномодальность распределений является, как правило, следствием наличия лишь одного стационарного состояния m0 для уравнения (1) (индуцированными шумом переходами в данном случае пренебрегаем, так как потеря устойчивости обществом достигается до их появления, которое предварительно выражается в значительном увеличении ширины распределений). Нетрудно видеть, что для рассмотренных нами моделей (А) и (В) это условие выполнено.
У2. Критерии “устойчивости” или “оптимальности” состояния СЭС, основанные на количественном сравнении “наиболее богатых” с “наиболее бедными” объектами (или подобные им) фактически сводятся к ограничениям на ширину D распределений Ps(x) (автомодельных распределений, т.к. такие критерии формулируются для относительных величин).
А так как D(s02) является монотонной функцией, то такие критерии могут быть формально представлены как[85]
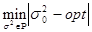 (10)
(10)
где s02=opt - такое оптимальное значение относительной интенсивности шума, при котором достигается наилучшее Ps(x).
У3. Требование роста m0=(c/d)1/(b-a) означает следующее: а). если c>d, то a®b. Таким образом, рост m0 может быть осуществлен как “тонкой балансировкой” внутри области ½1-a/b½<<1 (что может быть реализовано, например, “точным регулированием” налоговой политики, которая сказывается на величине b - см. Рис.1), так и ростом с (то есть более полным использованием информационных возможностей Человека), либо - обоими вместе. Уменьшения разности b-a>0 можно достичь либо увеличивая a, либо уменьшая b. Второй “сценарий” означает уменьшение налогового бремени, но обеспечивает только кратковременный успех, ибо инфраструктуры, необходимые для усиления синтеза информации и социализации ее в финансы остаются практически неизменными (к тому же, при a<1 характерное время T при c=const может даже возрастать с уменьшением d).
б). Если c<d, то вследствие a<b имеем ограничение сверху на m0<1, что ввиду рассмотрения нами размерных величин для m0 представляется бессмысленным. Таким образом, случай c<d для рассмотренных нами задач не может иметь место.
Итак, для роста m0 требуется: c>d и a®b, причем главное внимание надо уделять возрастанию как с, так и a (а “налоговое бремя” при этом может быть даже увеличено по абсолютной величине!).
Математически сказанное можно записать следующим образом. Введем пространства
 (11)
(11)
и
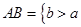 (12)
(12)
Отметим, что для белого шума пространство AB определяется с учетом конкретных особенностей моделей (А) и (В):
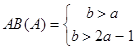
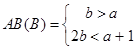 (13)
(13)
Тогда У3 примет вид

 (14)
(14)
Это условие часто с учетом сказанного выше можно переписать в виде
 (15)
(15)
Соотношения (4) - (8) записаны для данного иерархического уровня.
У4. Формализация данного условия требует уже информации о виде и структуре шума xt (или ht). Для белого шума это условие можно записать так:
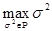 (16)
(16)
где R=[0,¥).
У5. Условие уменьшения T может быть записано как

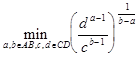 (17)
(17)
Представленная задача оптимального управления должна решаться каждый раз при переводе СЭС в новое состояние.
Выводы
Проведенное рассмотрение позволяет сделать следующие выводы.
1. Рассмотренный класс моделей позволяет формализовать описание многих сторон социально - экономических процессов и состояний, ранее выражавшихся лишь вербально. На основе проведенной формализации возникает возможность синтеза математических критериев для оптимизации управления СЭС разного уровня иерархии.
2. Представленные модели позволяют свести к сравнительно небольшому количеству параметров многие аспекты законодательного порядка, регулирующие широкий круг социально - экономического отношений (прежде всего - налоговых), уровень социально - экономического состояния общества (государства), образования, степень развитости экономики (в том числе - наличия необходимых инфраструктур), и т.п.
3. Введение “медленных” переменных t (с характерным временем изменчивости много больше T0={(1-a)c}-1m01-a) позволяет использовать полученные результаты путем введения зависимостей вида a(t), b(t), c(t), d(t),s2(t) и т.п.
4. Полученный способ описания допускает распространение на нестационарные случаи, но исследование может быть проведено, как правило, лишь численными методами или путем компьютерного моделирования.
5. Сформированный класс моделей позволяет как непосредственно произвести их количественную экспериментальную верификация, так и получить на их основе прогноз поведения числовых параметров, характеризующих СЭС.






