В основе дальнейшего изложения лежит понятие ранжировки. Ранжировка множества представляет собой упорядоченный набор его элементов (кортеж). Считается, что первый в ука-занном порядке элемент получает ранг 1, следующий за ним – ранг 2, и т.д., вплоть до послед-него элемента, который получает ранг m (m – это число элементов, или мощность исходного множества). Записываться ранжировки множества Ω = { x 1, …, xm } будут в виде
r: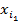 
… 
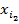
. (1)
Запись (1) означает, что на 1-ом месте в ранжировке r стоит элемент 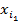, за ним – элемент 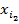, и так далее, вплоть до последнего элемента . Легко понять, что формально любая ранжиров-ка r задаёт отношение линейного Р порядка на том же множестве Ω. Именно, xPy тогда и только тогда, когда в ранжировке r элемент x встречается раньше, чем элемент y (т.е. x записан левее, чем y). Обратно, каждое отношение линейного порядка P на множестве Ω так же естественно определяет некоторую ранжировку r множества Ω.
Описанные ранжировки иногда называются строгими, чтобы отличать их от более общих ранжировок, при которых разные объекты могут получать одинаковые ранги. Таким образом, в общей, или нестрогой ранжировке все элементы исходного множества Ω разбиваются на несколько групп: Ω 1, Ω 2, …, Ωd, так что при этом все элементы из Ω 1 получают ранг 1, из Ω 2 – ранг 2, и т.д., вплоть до Ωd, все элементы которого получают ранг d. Нестрогие ранжировки определяют слабый порядок P (см. раздел 14-2.3) на множестве Ω. Именно, xPy тогда и только тогда, когда индекс множества Ωi, в которое входит элемент x, меньше индекса множества Ωj, в которое входит элемент y. Обратно, каждое отношение слабого порядка P на множестве Ω так же естественно определяет некоторую ранжировку r множества Ω. Для нестрогих ранжировок будем пользоваться обозначением
Ω 1 Ω 2 … Ωd. (2)
Определим рассматриваемое здесь понятие коллективного решения. Предполагается, что члены группы, состоящей из n участников (n > 2), выражают своё мнение относительно альтер-натив из множества Ω = { x 1, …, xm } (m ≥ 2), в виде строгих ранжировок ri этого множества Ω (i = 1, …, n). В ранжировке ri лучшая (с точки зрения i -го участника) альтернатива получает ранг 1, и т.д., вплоть до худшей альтернативы, которая получает ранг m. Под коллективным реше-нием будет пониматься некоторая (уже не обязательно строгая) ранжировка, которая построе-на, исходя из ранжировок, данных всеми участниками. Можно сказать, что она агрегирует их индивидуальные предпочтения и выражает коллективное мнение по поводу рассматриваемых альтернатив из Ω. Различные способы построения такого коллективного решения и излагаются в настоящей главе.
Главным признаком, по которому разделяются представленные в настоящей главе мето-ды, является вид используемой информация о ранжировках участников. В разделе 2 рассматри-ваются коллективные решения, построенные непосредственно по этим ранжировкам. В разделе 3 излагаются методы, использующие не сами исходные ранжировки, а определяемые ими чис-ленности некоторых групп участников. Остановимся на этом подробнее.
Любое множество участников назовём коалицией. Пусть a и b – любые две альтернативы. Обозначим через V (a, b) коалицию участников, считающих, что альтернатива a предпочтитель-ней, чем альтернатива b,т.е. a имеет мéньший ранг, чем b, в ранжировках участников из V (a, b). В разделе 3 излагаются методы, использующие при построении коллективного решения най-денные по исходным ранжировкам числа | V (a, b) | для всех пар альтернатив. Их выделение объ-ясняется не только важностью и распространённостью этих методов для построения коллективного решения, но и тем, что их аналоги и модификации можно применять и для упо-рядочивания альтернатив на основе одного бинарного отношения безотносительно к проблема-тике коллективных решений. Среди методов этой группы можно выделить методы, основанные только на информации о том, для каких пар альтернатив числа | V (a, b) | больше, чем n ⁄ 2. Эти широко распространённые методы называются методами, основанными на мажоритарном отношении.
Разумеется, проблематика коллективных решений гораздо шире вышеуказанной поста-новки. Можно сказать, что здесь рассматривается простейшее понятие коллективного решения. Однако и более сложные модели включают те же базовые элементы: виды индивидуальных предпочтений, вид коллективного предпочтения и само правило его построения.
