Напомним, что m -мерное пространство – это множество всех точек с m координатами (мы «живём» в 3-х мерном пространстве). Многомерное пространство бывает удобным для описа-ния объектов, характеризующихся несколькими параметрами или критериями. При этом оно обычно называется критериальным пространством.
Пусть Ω – множество n точек в многомерном пространстве:
Ω = { x 1, x 2, …, xn }.
Определим отношение Парето (обозначается через P) на множестве Ω следующим образом:
xPy ↔ (xi ³ yi, i = 1, …, m) и ($ j: xj > yj). (1)
В силу этого определения у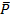 
х (т.е. y не «лучше» x по отношению Парето) означает, что хотя бы одна координата х больше, чем та же координата у. Множеством Парето на Ω называется множество всех мажорант по отношению Парето (см. определение мажоранты по бинарному отношению в разделе 14-3); оно обозначается через ΩP. Отношение и множество Парето факти-чески уже использовалось в пособии: в разделе 11-3 при удалени доминируемых строк и столб-цов в платёжной матрице; в разделе 13-2.3 при определении справедливых дележей.
Множество Парето названо по имени выдающегося ученого Вильфредо Парето (1848 –1923), впервые обратившего внимание на альтернативы, не уступающие друг другу по критери-альным оценкам, т. е. на альтернативы, из которых ни одна не доминирует другую. Напомним, что такие альтернативы находятся между собой в отношении несравнимости (см. определение в разделе 14-2.1).
По самому определению мажоранты, любые две альтернативы, входящие в мажоранту ΩP, несравнимы по отношению Р. Для выбора лучших из них необходимо использовать дополни-тельную информацию – естественно, от ЛПР и ∕ или экспертов. Некоторые возможности этого рассмотрены ниже в разделе 4. Но даже само выделение множества Парето оказывается весьма полезным. Понятно, что альтернативы, не входящие в множество Парето, можно просто не рас-сматривать. Для каждой из них есть не уступающая ей по всем критериям (и хотя бы по одному превосходящая) альтернатива из множества Парето ΩP. Доля элементов из множества Парето по сравнению с общим числом элементов из Ω обычно невелика (и тем меньше, чем больше число элементов в исходном множестве Ω). Подробнее это рассмотрено в разделе 3.
Алгоритм построения мажоранты по любому бинарному отношению R описан в разделе 14-3.1. Там предполагалось, что само бинарное отношение R задано в виде полного перечня за-писей вида xRy. Однако для задач в критериальном пространстве естественно считать, что все элементы множества Ω являются точками в критериальном пространстве Em. Поэтому алгоритм должен и найти все пары векторных оценок á x, y ñ, для которых верно xРy, и удалить все домини-руемые альтернативы. Всё это делается одним алгоритмом.
Заданноемножество m- мерных точек Ω = { x 1, x 2, …, xn } представляет собой вход алгоритма. Выходом является множество Парето ΩP.
Алгоритм 1. Выделение множества Парето.
1. Инициализация. Положим L = Ω, D =Æ, xb = x 1.
2. Точка xb сравнивается последовательно со всеми элементами списка L, кроме элемента x 1.
При сравнении элемента xb с элементом y возможны три случая:
а) xbPy; в этом случае элемент y удаляется из списка L; если в списке остался только один элемент, то переходим к шагу 4; в противном случае элемент Ошибка! Ошибка связи.Ошибка! Ошибка связи.Ошибка! Ошибка связи.Ошибка! Ошибка связи. xb сравнивается со следую-щим элементом списка L;
б) yPxb; в этом случае элемент xb удаляется из списка; если в списке остался только один элемент, то переходим к шагу 4; в противном случае xb = у; элемент xb сравнивается со следующим (после y) элементом списка L;
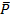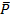в) xb y и у хb; далее элемент xb сравнивается со следующим элементом списка L.
3. При достижении конца списка положим D = D 
{ xb }, L = L 
{ xb }, xb = 1-ому элементу списка L. Возвращаеися к шагу 2.
4. Положим ΩP = D z, где z – единственный элемент списка L. Алгоритм 1 останавливается ■
Пример 1. Найтдём множество Парето ΩP для исходного множества альтернатив Ω = {(3,7,0), (4,5,1), (2,3,0), (3,7,3), (2,6,3), (4,5,2)}.Используем алгоритм 1.
1. Инициализация. Положим L = Ω = {(3,7,0), (4,5,1), (2,3,0), (3,7,3), (2,6,3), (4,5,2)}, D =Æ, xb = x 1 = (3,7,0).
2. Сравниваем xb =(3,7,0) с y =(4,5,1). Имеет место случай в). Переходим к следующему в списке элементу y = (2,3,0).
2. Сравниваем xb = (3,7,0) с y = (2,3,0). Поскольку (3,7,0) P (2,3,0), то имеет место случай а). Элемент (2,3,0) удаляется из списка, и получаем L ={(3,7,0), (4,5,1), (3,7,3), (2,6,3), (4,5,2)}. Пе-реходим к следующему (после удалённого) элементу y = (3,7,3).
2. Сравниваем xb = (3,7,0) с y = (3,7,3). Поскольку (3,7,3) P (3,7,0), то имеет место случай б). Удаляем из списка xb = (3,7,0) и получаем L ={(4,5,1), (3,7,3), (2,6,3), (4,5,2)}. Положим xb = (3,7,3) и переходим к следующему элементу y = (2,6,3).
2. Сравниваем xb = (3,7,3) с y = (2,6,3). Поскольку (3,7,3) P (2,6,3), то имеет место случай а).Элемент (2,6,3) удаляется из списка и получаем L ={(4,5,1), (3,7,3), (4,5,2)}. Переходим к следу-ющему (после удалённого) элементу y = (4,5,2)
2. Поскольку xb = (3,7,3) и y = (4,5,2) несравнимы, имеет место случай в). Поскольку достиг-нут конец списка, переходим к шагу 3.
3. Положим D = Æ { xb } = {(3,7,3)}. Удаляя (3,7,3) из списка L, получим L ={(4,5,1), (4,5,2)}. Положим xb = (4,5,1) и перейдём к шагу 2.
2. Сравниваем xb = (4,5,1) с y =(4,5,2). Поскольку (4,5,2) P (4,5,1), то имеет место случай б). Удаляем из списка xb = (4,5,1) и получаем xb = (4,5,2), L ={(4,5,2)}. Поскольку список L состоит из одного элемента(4,5,2), переходим на шаг 4.
4. Положим D = D {(4,5,2)}= {(3,7,3), (4,5,2)}■
Задание 1. Найти алгоритмом 1 множество Парето для следующих множеств точек
01. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,4), (1,4,3), (8,1,2)}
02. Ω ={(3,7,5), (4,5,-1), (2,3,0), (5,6,-4), (1,4,3), (8,1,2)}
03. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,-4), (-1,4,3), (8,1,2)}
04. Ω = {(3,7,5), (4,5,-1), (2,-3,0), (5,6,4), (1,4,3), (8,1,2)}
05. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,4), (1,4,-3), (8,1,2)}
06. Ω = {(3,7,5), (4,5,-1), (2,3,0), (-5,6,4), (1,4,3), (8,1,2)}
07. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,-4), (-1,4,3), (8,1,2)}
08. Ω = {(3,7,5), (4,5,-1), (2,3,0), (5,6,4), (1,4,3), (8,1,-2)}
09. Ω = {(3,7,5), (4,5,-1), (2,3,0), (5,6,-4), (1,4,3), (8,1,2)}
10. Ω = {(-3,7,5), (4,5,1), (2,3,0), (5,6,4), (1,4,3), (8,1,2)}
11. Ω ={(3,-7,5), (4,5,-1), (2,3,0), (5,6,-4), (1,4,3), (8,1,2)}
12. Ω = {(3,7,-5), (4,5,1), (2,3,0), (5,6,-4), (-1,4,3), (8,1,2)}
13. Ω = {(3,7,5), (-4,5,-1), (2,-3,0), (5,6,4), (1,4,3), (8,1,2)}
14. Ω = {(3,7,5), (4,-5,1), (2,3,0), (5,6,4), (1,4,-3), (8,1,2)}
15. Ω = {(3,7,5), (4,5,1), (2,3,0), (-5,6,4), (1,4,3), (8,1,2)}
16. Ω = {(3,7,5), (4,5,1), (-2,3,0), (5,6,-4), (-1,4,3), (8,1,2)}
17. Ω = {(3,7,5), (4,5,-1), (2,-3,0), (5,6,4), (1,4,3), (8,1,-2)}
18. Ω = {(3,7,5), (4,5,-1), (2,3,-0), (5,6,-4), (1,4,3), (8,1,2)}
19. Ω = {(3,7,5), (4,5,1), (2,3,0), (-5,6,4), (1,4,3), (8,1,2)}
20. Ω ={(3,7,5), (4,5,-1), (2,3,0), (5,-6,-4), (1,4,3), (8,1,2)}
21. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,4), (-1,4,3), (8,1,2)}
22. Ω = {(3,7,5), (4,5,-1), (2,-3,0), (5,6,4), (-1,4,3), (8,1,2)}
23. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,4), (1,-4,-3), (8,1,2)}
24. Ω = {(3,7,5), (4,5,-1), (2,3,0), (-5,6,4), (1,4,-3), (8,1,2)}
25. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,-4), (-1,4,3), (-8,1,2)}
26. Ω = {(3,7,5), (4,5,-1), (2,3,0), (5,6,4), (1,4,3), (8,-1,-2)}
27. Ω = {(3,7,5), (4,5,-1), (2,3,0), (5,6,-4), (1,4,3), (8,1,-2)}
28. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,4), (1,4,3), (8,-1,2)}
29. Ω ={(3,7,5), (4,5,-1), (2,3,0), (5,6,-4), (1,4,3), (-8,1,2)}
30. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,-4), (-1,4,-3), (8,1,2)}
31. Ω = {(3,7,5), (4,5,-1), (2,-3,0), (5,6,4), (1,-4,3), (8,1,2)}
32. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,6,4), (-1,4,-3), (8,1,2)}
33. Ω = {(3,7,5), (4,5,-1), (2,3,0), (-5,6,-4), (1,4,3), (8,1,2)}
34. Ω = {(3,7,5), (4,5,1), (2,3,0), (5,-6,-4), (-1,4,3), (8,1,2)}
35. Ω = {(3,7,5), (4,5,-1), (2,3,0), (-5,6,4), (1,4,3), (8,1,-2)}
36. Ω = {(3,7,5), (4,5,-1), (2,-3,0), (5,6,-4), (1,4,3), (8,1,2)}
37. Ω = {(3,7,5), (4,5,1), (-2,3,0), (5,6,4), (1,4,3), (8,1,2)}
38. Ω ={(3,7,5), (4,5,1), (2,3,0), (5,6,-4), (1,4,3), (8,1,2)}
39. Ω = {(3,7,5), (4,-5,1), (2,3,0), (5,6,-4), (-1,4,3), (8,1,2)}
40. Ω = {(3,7,5), (-4,5,-1), (2,-3,0), (5,6,4), (1,4,3), (8,1,2)}
41. Ω = {(3,7,-5), (4,5,1), (2,3,0), (5,6,4), (1,4,-3), (8,1,2)}
42. Ω = {(3,-7,5), (4,5,-1), (2,3,0), (-5,6,4), (1,4,3), (8,1,2)}
43. Ω = {(-3,7,5), (4,5,1), (2,3,0), (5,6,-4), (-1,4,3), (8,1,2)}
44. Ω = {(-3,7,5), (-4,5,-1), (2,3,0), (5,6,4), (1,4,3), (8,1,-2)}
45. Ω = {(3,7,5), (-4,5,-1), (-2,3,0), (5,6,-4), (1,4,3), (8,1,2)}
46. Ω = {(3,7,5), (4,5,-1), (-2,3,0), (-5,6,4), (1,4,3), (8,1,-2)}
47. Ω = {(3,7,5), (4,5,-1), (2,3,0), (-5,6,-4), (1,4,3), (8,1,2)}
48. Ω = {(3,7,5), (4,5,-1), (2,3,0), (5,6,4), (-1,4,3), (8,1,-2)}
49. Ω = {(3,7,5), (4,5,-1), (2,3,0), (5,6,-4), (-1,4,3), (-8,1,2)}
50. Ω = {(-3,7,5), (4,5,-1), (2,3,0), (5,6,4), (1,4,3), (-8,1,-2)}■
Во многих случаях надо не только выделить множество Парето из исходного множества, но и выделить множество Парето из оставшегося (после удаления 1-го множества Парето) мно-жества, и т.д. Эти последовательно выделяемые множества называются слоями или уровнями Парето. Продемонстрируем весь процесс на том же примере.
Пример 2. Для исходного множества Ω = {(3,7,0), (4,5,1), (2,3,0), (3,7,3), (2,6,3), (4,5,2)} множество Парето ΩP = {(3,7,3), (4,5,2)} (cм пример 1). Далее, Ω 1= Ω ΩP = {(3,7,0), (4,5,1), (2,3,0), (2,6,3)}. Выделяя тем же алгоритмом 1 из множества Ω 1 его паретовскую часть, находим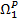 
= {(3,7,0), (4,5,1), (2,3,0), (2,6,3)} P = {(3,7,0), (4,5,1), (2,6,3)}. Поскольку Ω 2= Ω 1 
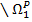= {(2,3,0)}, то окочательно получаем, что всего имеется три паретовских слоя: {(3,7,3), (4,5,2)}; {(3,7,0), (4,5,1), (2,6,3)} и {(2,3,0)}■
Задание 2. Для данных по оценкам 7-и учениц найти и нарисовать их паретовские уровни со всеми дугами, соединяющими только соседние уровни.
| Школьник | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра | ||||
| 2. Баранникова Елена | ||||
| 3. Кулакова Екатерина | ||||
| 4. Михайлова Елена | ||||
| 5. Морозова Мария | ||||
| 6. Перепечаева Арина | ||||
| 7. Полищук Наталья |
| Школьник | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра лександра | ||||
| 2. Баранникова Елена | ||||
| 3. Кулакова Екатерина | ||||
| 4. Михайлова Елена | ||||
| 5. Морозова Мария | ||||
| 6. Перепечаева Арина | ||||
| 7. Полищук Наталья |
| 1Школьник | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра | ||||
| 2. Баранникова Елена | ||||
| 3. Кулакова Екатерина | ||||
| 4. Михайлова Елена | ||||
| 5. Морозова Мария | ||||
| 6. Перепечаева Арина | ||||
| 7. Полищук Наталья |
| Школьник | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра | ||||
| 2. Баранникова Елена | ||||
| 3. Кулакова Екатерина | ||||
| 4. Михайлова Елена | ||||
| 5. Морозова Мария | ||||
| 6. Перепечаева Арина | ||||
| 7. Полищук Наталья |
| Школьник | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра | ||||
| 2. Баранникова Елена | ||||
| 3. Кулакова Екатерина | ||||
| 4. Михайлова Елена | ||||
| 5. Морозова Мария | ||||
| 6. Перепечаева Арина | ||||
| 7. Полищук Наталья |
| Школьник | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра | ||||
| 2. Баранникова Елена | ||||
| 3. Кулакова Екатерина | ||||
| 4. Михайлова Елена | ||||
| 5. Морозова Мария | ||||
| 6. Перепечаева Арина | ||||
| 7. Полищук Наталья |
| Школьник | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра лександра | ||||
| 2. Баранникова Елена | ||||
| 3. Кулакова Екатерина | ||||
| 4. Михайлова Елена | ||||
| 5. Морозова Мария | ||||
| 6. Перепечаева Арина | ||||
| 7. Полищук Наталья |
07■
| Школьница | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра | ||||
| 2. Баранникова Елена | ||||
| 3. Кулакова Екатерина | ||||
| 4. Михайлова Елена | ||||
| 5. Морозова Мария | ||||
| 6. Перепечаева Арина | ||||
| 7. Полищук Наталья |
Метод Подиновского
Выделение множества Парето, хотя и позволяет в значительной степени сократить число альтернатив, которые являются «кандидатами» для выбора лучших из них, всё же целесообраз-но рассматривать как первый этап такого выбора. Дело в том, что при наличии нескольких кри-териев для выбора лучших вариантов необходимо в той или иной форме использовать предпоч-тения лица, принимающего решения (ЛПР). Выявление предпочтений ЛПР и разработка осно-ванных на них алгоритмов выбора является центральной и наиболее трудной проблемой в при-нятии решений. Метод, предложенный более 30 лет назад современным российским учёным В.В. Подиновским(и с тех пор многократно усовершенствованный и модифицированный), явля-ется одним из наиболее эффективных в этой важной области. Здесь даётся его сжатое и упро-щённое изложение.
Как и выше в настоящей главе, речь идёт об объектах (учениках, фирмах, автомобилях, бизнес-планах и т.д.), которые оцениваются по нескольким критериям. Принципиальным в из-лагаемом ниже подходе является однородность критериев. Это означает, что у всех критериев имеется единая (общая) шкала. Более того, должно выполняться следующее условие однород-ности: каждая градация шкалы должна отражать одинаковый уровень предпочтений для каждо-го из критериев. Это условие выполняется, в частности, в том случае, когда градации являются вербальными (словесными). При этом они имеют смысл, одинаковый для всех критериев, на-пример, «превосходно», «отлично», …, «отвратительно». Обычно градации нумеруются в по-рядке возрастания предпочтительности. Нужно подчеркнуть, что номера градаций, которые часто называют баллами, отражают лишь их упорядоченность по предпочтению. Поэтому с числами – номерами градаций нельзя производить арифметические операции для получения ка-ких-либо иных оценок предпочтений. Например, бессмысленно говорить, будто при отличной оценке успеваемость (знания, умения, навыки и компетенции) в 2,5 раза выше, чем при неудов-летворительной. По этой причине рассматриваемые шкалы являются порядковыми (см.раздел 1.1).
Итак, далее предполагается (и специально не оговаривается), что все критерии однород-ны, т.е. они имеют единую порядковую шкалу. В качестве основного примера будем рассматри-вать оценки семи учениц по четырём предметам (см. таблицу 1, совпадающую с вариантом 08 из задания 2), имея в виду, что все рассуждения справедливы для любых объектов, оценивае-мых по однородным критериям.
Таблица 1
| Школьница | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра | ||||
| 2. Баранникова Елена | ||||
| 3. Кулакова Екатерина | ||||
| 4. Михайлова Елена | ||||
| 5. Морозова Мария | ||||
| 6. Перепечаева Арина | ||||
| 7. Полищук Наталья |
3.1. Понятие качественной важности. Под качественной важностью критериев будем понимать качественные оценки их относительной важности. Суждение «критерий К i важнее критерияKj» будем обозначать «словом» i 
j, а суждение «критерии Ki и Kj равноважны» − «словом»i ≈ j.Дляобозначения качественной информация о важностибудет использоваться буква греческого алфавита Θ (тэта). Она формируется накопленными (полученными от ЛПР, экспертов и / или других источников) сведениями о том, что некоторые критерии одинаковы по важности и что одни критерии важнее других, т.е. сообщениями вида i ≈ j и i j. Например, если стало известно, что первый критерий важнее второго, а второй и третий критерии равно-важны, то Θ = {1 2, 2 ≈ 3}.
Обратимся теперь к центральному вопросу точного определения понятий равенства и пре-восходства критериев в важности.Предположим, что школьницы изучали всего два учебных предмета, так что каждая школьница получила всего две итоговые оценки. Если для характе-ристики общей успеваемости достаточно (и так нередко делается в жизни) перечислить полу-ченные ими оценки в произвольном порядке, не указывая при этом, какая оценка относится к тому или иному предмету (т.е. сказать, например, что у этой школьницы пятёрка и тройка, а у той − пятёрка и четвёрка), то это и означает, что каждый из предметов имеет одинаковую важ-ность. Если же это не так, причем считается, что из любых двух школьниц, имеющих одинако-вые пары оценок, лучше учится та, у которой более высокая оценка по определенному предме-ту, то этот предмет важнее другого. Если предметов более двух, то сравнивать относительную важность двух выбранных предметов можно путем сопоставления общей успеваемости таких школьниц, которые имеют одинаковые пары оценок по этим предметам, но по всем остальным предметам оценки у них должны быть одинаковыми.
Идеи разобранного примера лежат в основе следующих определений. В них под xij пони-мается векторная оценка, полученная извекторной оценки х перестановкой её компонент xi и xj. Например, если x = (5,4,3,4), то х 14 = (4,4,3,5) и х 23 = (5,3,4,4).
Введём два основных определения. Критерии Ki и Kj равноважны, или одинаково важ-ны, когда любые две векторные оценки х и xij одинаковы по предпочтению.Критерий Ki важ-нее критерия Kj,когда всякая векторная оценка х, в которой xi > xj,предпочтительнее, чем xij. Согласно первому из этих определений, сообщениеi ≈ jсвязывает векторные оценки х и у, та-кие, что у =xij, отношением безразличия I i≈j.Согласно второму определению, сообщение i > j связывает векторные оценки х и у, такие, что xi > xj, у =xij, отношением предпочтения Pi > j. Например, верно (5,4,3,4) P 1>2(4,5,3,4), поскольку вторая векторная оценка получается из первой перестановкой её первых двух компонент, причем именно в первой векторной оценке на пер-вом месте (как значение более важного критерия) стоит 5 − бóльшее из двух чисел 4 и 5. Ины-ми словами, указанная перестановка приводит к ухудшению первой векторной оценки.Верно также (5,4,3,4) I 2≈3(5,3,4,4). Действительно, здесь вторая векторная оценка получена из первой перестановкой второй и третьей компонент, а второй и третий критерии равноважны. Поэтому такая перестановка не приводит к изменению предпочтений. Но вот (5,4,3,4) I 2≈3(5,3,5,4) неве-рно, поскольку 2-ая векторная оценка не получена из 1-ой перестановкой 2-ой и 3-ьей коорди-нат.
Заметим очень важное обстоятельство. Указанные два правила можно применять для сравнения двух векторных оценок только тогда, когда одна из них получена перестановкой двух координат из другой. Если одна оценка получена перестановкой нескольких координат, то надо построить цепочку векторов, соединяющую две данные векторные оценки, так, чтобы пра-вила можно было бы применять к каждой паре соседних оценок. Если же одна векторная оцен-ка не может быть получена никакой перестановкой из другой (например, (5,4,3,3) и (4,5,3,4)), то иногда можно применять правило Парето P: одна оценка не меньше другой по всем координа-там и при этом хотя бы по одной координате строго больше. Такие пары можно «встраивать» в цепочки. Примеры будут даны ниже.
3.2.Использование качественной информации о важности критериев для сравнения пары векторных оценок. Накопленную качественную информацию о важности Θ нужно про-верять на непротиворечивость, поскольку в неё могут вкрасться ошибки. Противоречивость проявляется в том, что при помощи сообщений из Θ можно составить цикл, приводящий к зак-лючению, что некоторый критерий важнее самого себя. Тогда соответствующие сообщения на-до проверить и скорректировать. Так, если Θ содержит сообщения 1 2,2 3, 3 1, то отсю-да будет формально вытекать, например, что 1 1. Следовательно, по крайней мере, одно из трёх суждений в Θ ошибочно. Если при проверке выяснится, что неверно суждение 3 1, то его нужно заменить на 1 3. Известны формальные методы нахождения таких циклов, но здесь они не рассматриваются. Далее предполагается, что рассматриваемые наборы сообщений из Θ не содержат про-тиворечий.
Пример 3. Построение цепочки оценок. Пусть в двухкритериальной задаче известно, что первый критерий важнее второго, т.е. Θ = {1 2}. Понятно, что для векторных оценок (5,3) и (2,4) неверно (5,3) P 1>2(2,4) просто потому, что 2-ая оценка не получена из 1-ой перестановкой координат. Неверно также, что (5,3) P (2,4), поскольку 2-ая координата у первой оценки меньше, чем у второй: 3 < 4. Однако можно составить цепочку из двух звеньев: верных соотношений
(5,3) P 1>2(3,5) и (3,5) P (2,4).
Это и означает, что оценка (5,3) превосходит (с учётом имеющейся информации Θ о сравни-тельной важности критериев) оценку (2,4). Далее используем для этого факта запись хPΘу ■
Однако подобные цепочки можно построить не всегда. Например, при той же информа-ции Θ = {1 2} невозможно связать цепочкой оценки (5,3) и (4,5). Действительно, по правилу 1 можно утверждать, что (5,3) P 1>2(3,5). Далее, можно утверждать, что (4,5) P (3,5). Но цепочка не выстраивается, поскольку здесь имеются только превосходства «в разные стороны»: обе оцен-ки превосходят одну и ту же оценку (3,5), что не несёт никакой информации о сравнении ис-ходных оценок. Легко сформулировать общие утверждения.
1. Если имеются две векторные оценки, такие, что сумма координат у первой не больше, чем сумма координат у второй, то отношение Парето P не встраивается ни в какую цепочку, соединяющую первую оценку со второй.
2. Если имеются две векторные оценки, такие, что сумма координат у первой меньше, чем сумма координат у второй, то первая оценка не может превосходить вторую.
Первое утверждение очевидно в силу того, что у любой оценки, превосходящей по Парето дру-гую, сумма координат обязательно больше.Второе утверждение следует из того, что правила 1 и 2 применяются только к парам оценок, полученным одна из другой перестановкой двух коор-динат. Значит, при произвольной длине цепочек из таких оценок сумма координат остаётся по-стоянной. А применение правила Парето может только уменьшить сумму координат. Заметим, что эти утверждения ничего не говорят о сравнимости произвольных оценок с совпадающими суммами координат.
Пример 4. Более сложный случай. Рассмотрим 5-ую и 6-ую оценки из таблицы 1: (5,4,3,5) и (3,5,4,4). Предположим, что имеется следующая информация о важности критериев: Θ = {1≈2, 2 3,3≈4}.Попробуем сравнить указанные оценки. Имеем
(5,4,3,5) P 1>2(5,3,4,5) I 1≈2(3,5,4,5) I 3≈4(3,5,5,4) P (3,5,4,4).
При 1-ом сравнении использовано превосходство в важности между 2-ым и 3-ьим критериями, при 2-ом сравнении – равноценность 1-го и 2-го критериев, при 3-ьем сравнении – равноцен-ность 3-го и 4-го критериев, при 4-ом сравнении – превосходство по Парето между соответст-вующими оценками ■
Подчеркнем двоякую роль построенной в примере 4 цепочки и подобных ей. С одной сто-роны, такая цепочка от x к у показывает, что верно хРΘу. С другой стороны, она позволяет на-глядно и ясно объяснить, причем в терминах собранных сведений о предпочтениях, почему х предпочтительнее, чем у. Ив этом ещё одно существенное преимущество рассматриваемых ме-тодов перед теми, которые опираются на построение обобщенных критериев. Поэтому подоб-ного рода цепочки будем называть объясняющими. Понятно, что в роли объясняющей жела-тельно иметь цепочку возможно меньшей длины.
Конечно, есть формальные методы, находящие цепочки минимальной длины или устанав-ливающие отсутствие требуемых объясняющих цепочек. Алгоритм их построения будет изло-жен в сдедующем разделе.
Рассмотрим теперь 2-ую и 7-ую оценки из таблицы 1: (3,4,4,3) и (3,5,3,3). Для этих двух оценок не существует связывающих их объясняющих цепочек. Поскольку суммы координат у них одинаковые, то отношение Парето не может быть встроено в такую цепочку (утверждение 1). Поскольку вторая оценка не получена перестановкой координат из первой (в неё входит 5, которой нет в первой оценке), то применением правил 1 и 2 в любом порядке и количестве нельзя получить требуемого сравнения. Заметим, что этот вывод остаётся в силе для любой информации о важности критериев Θ.
Однако можно привести пример, когда информация Θ существенно влияет на сравнение одной и той же пары векторных оценок. Рассмотрим снова 5-ую и 6-ую оценки из таблицы 1: (5,4,3,5) и (3,5,4,4). Предположим, что имеется следующая информация о важности критериев: Θ = {1≈2, 3≈4},т.е. теперь нет информации о сравнении критериев 1 и 2 с критериями 3 и 4. Поэтому у нас нет возможности менять местами любую из двух первых координат с любой из двух последних. Это значит, что на двух последних местах в любой оценке, входящей в цепочку с началом (5,4,3,5), может стоять только 3,5 или 5,3. А на двух последних местах в заключительной оценке (3,5,4,4) стоят 4,4. Поскольку и 3,5, и 5,3 несравнимы по Парето с 4,4, то и сами оценки несравнимы.
В заключение этого раздела рассмотрим крайние случаи.
1. Если имеется информация о равноважности всех критериев, то вопрос о сравнении двух векторных оценок х и у решается следующим образом. Все координаты оценки х упорядочива-ются в порядке невозрастания, т.е. каждая следующая координата не превосходит предыдущую (равна или меньше). Полученный вектор обозначим через х ↓. Аналогично определяем вектор у ↓. Оценка х лучше оценки у (хPΘу) тогда и только тогда, когда х ↓ Pу ↓.
2. Информация о сравнительной важности критериев отсутствует (Θ =Æ). Тогда P Ø = P (т.е. одна оценка лучше другой тогда и только тогда, когда она доминирует её по Парето).
3.3. Алгоритм сравнения двух векторных оценок по отношениям Подиновского. В настоящем разделе приводится алгоритм построения объясняющей цепочки для двух любых векторных оценок x, y и любой информации Θ рассматриваемого типа. В результате работы алгоритма либо строится требуемая цепочка, либо устанавливается её отсутствие. Рассматрива-ются два случая:
А) S (x) = S (y) и х ↓ = y ↓;
Б) S (x) > S (y).
В остальных случаях, как было указано выше, ответы очевидны и не требуют специальных ал-горитмов.
Рассмотрим случаи А) и Б) по отдельности.
А). Если S (x) = S (y) и х ↓ = y ↓, то надо тщательно и терпеливо выписать всё, что можно по-лучить из вектора x с помощью цепочек допустимых перестановок. Для этого предлагается спе-циальный алгоритм 2А.
Алгоритм 2А. Алгоритм состоит в последовательном записывании информации в строчки по определённым правилам.
Шаг 0. В верхнюю (0-ую) строчку напишем исходный вектор x.
Шаг i (i >0). В i -ую строчку последовательно записываются все векторы, которые можно полу-чить из всех векторов, записанных в (i− 1)-ую строчку, одной допустимой перестановкой коор-динат. (Напомним, что допустимая перестановка координат – это перестановка двух координат s и t, если они указаны в Θ как равноценные или перестановка двух координат с номерами s и t, если указано, что s важнее t, и при этом s -ая координата больше, чем t -ая). При вписывании во все строчки, кроме 0-ой, вписывается слева направо следующие наборы: вектор из предыдущей (i− 1)-ой строчки, символ операции (превосходство Ps > t или равноценность I s≈t), новый вектор (полученный из записанного слева от знака операции перестановкой координат).
При вписывании проверяются три условия:
а) если получившийся вектор уже ранее вписывался на одном из шагов с 0-го до i -го, то ничего не вписывается;
б) если получившийся вектор совпадёт с заданным вектором y, то алгоритм останавливается.
в) если все векторы из (i− 1)-ой строчки проверены и никаких записей в i -ую строчку не сде-лано, алгоритм останавливается ■
Работа алгоритма 2А будет ниже продемонстрирована на примерах.
Если алгоритм 2А останавливается в соответствии с условием б), то объясняющая цепочка строится от конца к началу, переходя от правых частей записей к левым и поднимаясь к пре-дыдущим строкам. Причём, если в эту цепочку не входит ни одного отношения вида Pi > j, то это значит, что векторы х и y равноценны по отношению PΘ. Если в эту цепочку входит хотя бы одно отношение вида Pi > j, то это значит, что x превосходит y по отношению PΘ и при этом y не превосходит x по отношению PΘ. Построенная объясняющая цепочка является кратчайшей.
Заметим, что в случае остановки алгоритма по условию в) никакого вывода о превосходс-тве y над x или об отсутствии такого превосходства сделать нельзя. Надо применить описанный выше алгоритм к векторам y и x в указанном порядке (т.е. начинать построения с y).
Пример 5. Пусть Θ = {3 2, 1 ≈ 3}. Сравним два вектора: x= (5,3,4,5) и y = (4,5,3,5).Поскольку S (x) = S (y) и х ↓ = y ↓, то необходимо применить алгоритм 2А.
В данном случае имеем (по строчкам)
1. (5,3,4,5)
2. (5,3,4,5) I 1≈3(4,3,5,5), (5,3,4,5) P 3>2(5,4,3,5).
3. (4,3,5,5) P 3>2(4,5,3,5).
Алгоритм останавливается, так как получившийся вектор (4,5,3,5) = y. Вся цепочка такова:
x = (5,3,4,5) I 1≈3(4,3,5,5) P 3>2(4,5,3,5) = y.
Так как в эту цепочку входит отношение превосходства P 3>2, то в соответствии с описанием ал-горитма x превосходит y по отношению PΘ, и при этом y не превосходит x ■
Пример 6. Пусть снова Θ = {3 2, 1≈ 3}.Сравним тот же вектор x = (5,3,4,5) с другим вектором y = (3,5,5,4). Поскольку S (x) = S (y) и х ↓ = y ↓, то необходимо применить алгоритм 2А. В данном случае имеем (по строчкам)
1. (5,3,4,5)
2. (5,3,4,5) I 1≈3 (4,3,5,5), (5,3,4,5) P 3>2 (5,4,3,5).
3. (4,3,5,5) P 3>2 (4,5,3,5), (5,4,3,5) I 1≈3 (3,4,5,5).
4. (4,5,3,5) I 1≈3 (3,5,4,5) (применение к (3,4,5,5) отношения P 3>2 приводит к уже найденному (3,5,4,5)).
Понятно, что новых векторов из (3,5,4,5) не получим: P 3>2 неприменимо, так как на 3-ем месте стоит 4, на 2-ом – 5 и 4 < 5. А применение I 1≈3 приводит к тому, что уже было.В соответствии с описанием алгоритм останавливается. При этом установлено, что вектор (5,3,4,5) не превосходит вектор (3,5,5,4)по отношению PΘ ■
Пример 7. Сравним те же два вектора в обратном порядке, т.е. начнём с (3,5,5,4). В соот-ветствии с алгоритмом имеем
1. (3,5,5,4).
2. (3,5,5,4) I 1≈3 (5,5,3,4).
Больше ни одного нового вектора получить нельзя, так как P 3>2 неприменимо, а I 1≈3 приводит к тому, что уже было. Поэтому в данном случае вектор (3,5,5,4) не превосходит вектор (5,3,4,5)
по отношению PΘ. Вспоминая (см. пример 6), что вектор (5,3,4,5) также не превосходит вектор (3,5,5,4), то можно со всей определённостью сказать, что они несравнимы по этому отношению ■
Пример 8. Пусть теперь Θ = {3 2, 1≈3, 4 1}. Рассмотрим те же самые векторы x = (5,3,4,5) и y = (3,5,5,4). Попробуем сравнить их, используя бóльшую информацию Θ. В соответствии с тем же алгоритмом 2А получаем
1. (5,3,4,5)
2. (5,3,4,5) I 1≈3(4,3,5,5), (5,3,4,5) P 3>2 (5,4,3,5).
3. (4,3,5,5) P 3>2(4,5,3,5), (4,3,5,5) P 4>1(5,3,5,4), (5,4,3,5) I 1≈3 (3,4,5,5).
4. (4,5,3,5) P 4>1(5,5,3,4), (4,5,3,5) I 1≈3(3,5,4,5), (3,4,5,5) P 4>1(5,4,5,3).
5. (5,5,3,4) I 1≈3(3,5,5,4),
Вектор (3,5,5,4) появился в 5-ой строчке. Это означает, что найдена объясняющая цепочка x = (5,3,4,5) I 1≈3 (4,3,5,5) P 3>2 (4,5,3,5) P 4>1 (5,5,3,4) I 1≈3(3,5,5,4) = y.
Таким образом, на основе информации Θ = {3 2, 1≈3, 4 1} о сравнительной важности критери-ев можно утверждать, что (5,3,4,5) PΘ (3,5,5,4), т.е. набор оценок (5,3,4,5) является более пред-почтительным, чем набор (3,5,5,4). Заметим, что просто «глазами» найти такую цепочку было бы затруднительным ■
Б. Перейдём теперь к случаю Б: S (x) > S (y). В этом случае возможны только два ответа: xPΘy или x и y несравнимы. Для выяснения ответа используется алгоритм 2Б, в большой степе-ни напоминающий алгоритм 2А.
Алгоритм 2Б.
Шаг 0. В верхнюю (0-ую) строчку напишем исходный вектор x.
Шаг i (i >0). В i -ую строчку последовательно записываются все векторы, которые можно полу-чить из всех векторов, записанных в (i− 1)-ую строчку, одной допустимой перестановкой коор-динат. (Напомним, что допустимая перестановка координат – это перестановка двух координат s и t, если они указаны в Θ как равноценные или перестановка двух координат с номерами s и t, если указано, что s важнее t, и при этом s -ая координата больше, чем t -ая). При вписывании во все строчки, кроме 0-ой, вписывается слева направо следующие наборы: вектор из предыдущей (i− 1)-ой строчки, символ операции (Ps > t или равноценности I s≈t), новый вектор (полученный из записанного слева от знака операции перестановкой координат).
При вписывании проверяются три условия:
а) если получившийся вектор уже ранее вписывался на одном из шагов с 0-го до i -го, то ничего не вписывается;
б) если получившийся вектор превосходит по отношению Парето заданный вектор y, то алго-ритм останавливается.
в) если все векторы из (i− 1)-ой строчки проверены и никаких записей в i -ую строчку не сде-лано, алгоритм останавливается■
Работа алгоритма 2Б будет ниже продемонстрирована на примерах.
Если алгоритм 2Б останавливается в соответствии с условием б), то объясняющая цепочка строится от конца к началу, переходя от правых частей записей к левым и поднимаясь к преды-дущим строкам. В отличие от алгоритма 1, в этом случае всегда x превосходит y по отношению PΘ и при этом y никогда непревосходит x по отношению PΘ. Построенная объясняющая це-почка является кратчайшей.
Заметим, что в случае остановки алгоритма 2Б по условию в), в отличие от алгоритма 2А, можно с уверенностью сделать вывод о несравнимости векторов x и y: в силу условия S (x) > S (y) вектор y не может превосходить вектор x.
Пример 9. Пусть Θ = {3 2, 1 ≈ 3}. Сравним два вектора: x = (5,3,4,5) и y = (4,5,3,4). Поскольку S (x) > S (y), то необходимо применить алгоритм 2Б.
В данном случае имеем (по строчкам)
1. (5,3,4,5)
2. (5,3,4,5) I 1≈3(4,3,5,5), (5,3,4,5) P 3>2(5,4,3,5).
3. (4,3,5,5) P 3>2(4,5,3,5).
Алгоритм останавливается, так как получившийся вектор (4,5,3,5) P (4,5,3,4) = y. Вся цепочка та-кова:
x = (5,3,4,5) I 1≈3 (4,3,5,5) P 3>2 (4,5,3,5) P (4,5,3,4)= y.
В соответствии с описанием алгоритма 2Б x превосходит y по отношению PΘ, и при этом y не превосходит x ■
Пример 10. Пусть снова Θ = {3 2, 1 ≈ 3}. Сравним тот же вектор x = (5,3,4,5) с другим вектором y = (3,5,5,3). Поскольку S (x) > S (y), то необходимо применить алгоритм 2Б.
В данном случае имеем (по строчкам)
1. (5,3,4,5)
2. (5,3,4,5) I 1≈3 (4,3,5,5), (5,3,4,5) P 3>2 (5,4,3,5).
3. (4,3,5,5) P 3>2 (4,5,3,5), (5,4,3,5) I 1≈3 (3,4,5,5).
4. (4,5,3,5) I 1≈3 (3,5,4,5).
Понятно, что новых векторов из (3,5,4,5) не получим: P 3>2 неприменимо, так как на 3-ем месте стоит 4, на 2-ом – 5 и 4 < 5. А применение I 1≈3 приводит к тому, что уже было.
В соответствии с описанием алгоритм 2Б останавливается. При этом установлено, что вектор (5,3,4,5) не превосходит вектор (3,5,5,3) по отношению PΘ ■
Пример 11. Пусть теперь Θ = {3 2, 1≈3, 4 1}. Рассмотрим те же самые векторы x = (5,3,4,5) и y = (3,5,5,3). Попробуем сравнить их, используя бóльшую информацию Ω. В соответствии с тем же алгоритмом 2Б получаем
1. (5,3,4,5)
2. (5,3,4,5) I 1≈3(4,3,5,5), (5,3,4,5) P 3>2 (5,4,3,5).
3. (4,3,5,5) P 3>2(4,5,3,5), (4,3,5,5) P 4>1(5,3,5,4), (5,4,3,5) I 1≈3 (3,4,5,5).
4. (4,5,3,5) P 4>1(5,5,3,4), (4,5,3,5) I 1≈3(3,5,4,5), (3,4,5,5) P 4>1(5,4,5,3).
5. (5,5,3,4) I 1≈3(3,5,5,4),
Алгоритм останавливается, так как появившийся в 5-ой строчке вектор (3,5,5,4) превосходит по Парето (3,5,5,3) = y. Вся цепочка такова:
x = (5,3,4,5) I1≈3 (4,3,5,5) P3>2 (4,5,3,5) P4>1 (5,5,3,4) I1≈3(3,5,5,4) P(3,5,5,3) = y.
В соответствии с описанием алгоритма 2 x превосходит y по отношению PΘ, и при этом y не превосходит x ■
Задание 3. При Θ = {3 2, 1≈3, 4 3} сравнить все пары оценок из таблиц задания 2 ■
Предметный указатель
Критериев,
однородность
равноважность
равноценность
Критерий,
зависимый
независимый
Отношение
безразличия
предпочтения
Оценка
векторная
многокритериальная
по критерию
Парето,
множество
отношение
Подиновского,
метод
отношения
Пространство, критериальное
Срез верхний
нижний
Шкала,
идеальная
интервальная
порядковая
пропорциональная
Коллективные решения
1. Модель коллективного решения
2. Правила на основе ранжировок
3. Правила на основе численности коалиций
4. Предметный указатель
