7. (
х)[ 
(х)→ 
(x)] º ( х) (х)→( х) (x)
8. ( х)[ (х) 
(x)] º ( х) (х) 
( х) (x) ■
Задание 5. Написать отрицания следующих высказываний
1. У каждой собаки есть свой день
2. На равнинах Испании сегодня нет дождей
3. Некоторые книги длиннее, чем эта книга
4. Ни один мастер по ремонту компьютеров не умеет играть в «блэкджек»
5. Некоторым людям всегда везёт
6. Каждый иногда любит кого-то
7. Все любят победителя
8. Все мужчины созданы равными
9. Некоторые ученики из нашего класса ездили на загородную экскурсию ■
Задание 6. Для изображений из примера 15 отметить одной (или несколькими) буквами группу или группы картинок, удовлетворяющих условиям:
1. Ни одна картинка не имеет рамки
2. По меньшей мере одна картинка не имеет рамки
3. Не каждая картинка имеет рамку
4. По меньшей мере одна картинка имеет рамку
5. Нет картинок, которые не имеют рамки
6. Все картинки не имеют рамки
7. Не каждая картинка не имеет рамки ■
Предметный указатель
Выражение
Квантор,
общности,
по переменной
существования,
по переменной
Квантора навешивания операция
Константа
Константыравносильные
Переменная,
высказывательная
несущественная
свободная
связанная
фиктивная
числовая
Переменной,
значения допустимые
область значений
Форм,
равносильность
неравносильность
Форма,
высказывательная
одноместная,
всюду определённая
нигде не определённая
равносильная константе
функциональная
числовая
s-местная,
всюду определённая
нигде не определённая
Формы, равносильные
высказывательной область истинности
функциональной область прибытия
Глава 5. Булева алгебра
1. Понятие булевой функции
2. Функции и формулы
3. Формальный анализ высказываний
4. Булевы функции для описания систем голосования
5. Код Хемминга
6. Задания
7. Предметный указатель
Понятие булевой функции
Булевы функции названы в честь английского математика XIX века Джорджа Буля, кото-рый впервые применил алгебраические методы для решения логических задач. Иногда они на-зываются также логическими функциями и функциями алгебры логики. Булевы функции находят применение в вычислительной технике, логике, теории управления, принятии решений и многих разделах информатики.
Обозначим через В двухэлементное множество {0,1}, состоящее из двух символов 0 и 1. Тогда Вп = В×В×... ×В (n сомножителей) – это множество всех кортежей длины n, компоненты которых равны 0 или 1. По определению, В 1= В = {0,1}. Обратим особое внимание на тот факт, что 0 и 1 – это, вообще говоря, не числа ноль и один, а формальные символы, некоторые опера-ции над которыми действительно напоминают обычные арифметические операции сложения и умножения, однако другие операции над ними совсем не похожи на арифметические.
Определим булевы функции, используя общую конструкцию функции из раздела 4-1.1. Булевой функцией называется функция с областью отправления Вп и областью прибытия В. Число n может быть произвольным натуральным числом: 1, 2, …. Возвращаясь к привычным обозначениям, можно сказать, что булева функция является функцией от n переменных, прини-мающих значения из множества В = {0,1}; значения булевой функции принадлежат тому же са-мому двухэлементному множеству В. Если не указано противное, булевы функции будем счи-тать определёнными на всех наборах из Вп. Это значит, что область определения булевой функ-ции совпадает с её областью отправления.
Имеется несколько различных способов представления и интерпретации булевых функций. В данной главе рассматривается табличное представление, а также представление с помощью булевых или логических формул.
1.1. Табличное представление. Булевы функции от небольшого числа переменных удоб-но представлять с помощью таблиц. Таблица для функции f (x 1, …, xn) имеет п + 1 столбец. В первых n столбцах указываются значения переменных x 1, …, xn, а в (n + 1)-ом столбце – значе-ние f (x 1, …, xn) функции f на этом наборе значений.
Таблица.1. Табличное представление функции f (x 1, …, xn)
| x 1 | ...... | xn –1 | xn | f (x 1, …, xn –1, xn) |
| ...... | f (0, …, 0, 0) | |||
| ...... | f (0, …, 0, 1) | |||
| ...... | f (0, …, 1, 0) | |||
| ...... | ..... | |||
| ...... | f (1, …, 1, 1) |
Наборы переменных в строках обычно располагаются в лексикографическом порядке:
(α 1, …, αn) 
(β 1, …, βn) ↔ i 
{1, …, n }, такое, что при всех j < i αj = βj и αi < βi. (1)
Если эти наборы рассматривать как записи чисел в двоичной системе счисления, то 1-ая строка является записью числа 0, 2-ая – числа 1, 3-я – числа 2,..., а последняя – числа 2 n –1. Типичное представление булевой функции от трёх переменных даётся в таблице 2. В этой таблице, как и во всех последующих таблицах, задающих булевы функции, наборы переменных расположены в лексикографическом порядке. Обратим особое внимание на удобство такого расположения. Его не надо запоминать. Просто в последнем (самом правом) столбце значения меняются, начиная с нуля, через одну позицию; в предпоследнем столбце, начиная с двух нулей, через две позиции, и т.д., вплоть до первого столбца, в котором в первой половине позиций стоят нули, а во второй половине – единицы. Другие важные свойства наборов, расположенных именно в таком порядке, будут рассмотрены в разделе 5.
Таблица 2. Функция от трёх переменных
| x 1 | x 2 | x 3 | f (x 1, x 2, x 3) |
При больших п табличное представление становится громоздким. Например, для функции от 10 переменных потребуется таблица с 1024 строками. Но для малых п (п = 2, 3, 4) оно достаточ-но наглядно.
1.2. Булевы функции от одной и двух переменных. Прежде чем двигаться дальше и гово-рить о других представлениях булевых функций, необходимо детально рассмотреть булевы функ-ции от одной и двух переменных. Функции от одной переменной записаны в таблице 3. Этих функций – четыре:
Таблица 3. Булевы функции от 1-ой переменной
| x | φ 0 | φ 1 | φ 2 | φ 3 |
Левый столбец содержит два значения переменной x. Следующие 4 столбца определяют все 4 фун-кции от одной переменной. Функции φ 0 и φ 3 – константы 0 и 1; их значения не зависят от значения переменной x. В конце раздела 4-1.1 такие переменные названы несущественными. Функция φ 1 «повторяет» x: φ 1(x) = x. Функция φ 2(x) называется отрицанием x. Для отрицания будет использо-ваться тот же знак Ø, который использовался в таблицах 1-1 и 1-2 для отрицания высказываний. Иногда для отрицания используются также обозначения 
, x 0, ~ x.
Отличие от введённой в разделе 1-2 операции отрицания состоит в том, что там отрицание относилось только к высказываниям и их истинностным значениям. Здесь отрицание относится к формальным символам 0 и 1, для которых интерпретация их как истинностных значений F и T является хотя и часто используемой, но далеко не единственной. То же самое относится и к булевым функциям от любого числа переменных.
Рассмотрим теперь логические функции от двух переменных. Их число равно 16. Все они записаны в таблице 4.
Таблица 4. Булевы функции от 2-ух переменных
| x 1 | x 2 | ψ 0 | ψ 1 | ψ 2 | ψ 3 | ψ 4 | ψ 5 | ψ 6 | ψ 7 | ψ 8 | ψ 9 | ψ 10 | ψ 11 | ψ 12 | ψ 13 | ψ 14 | ψ 15 |
Два левых столбца содержат все четыре набора переменных: (0, 0), (0, 1), (1, 0), (1, 1), расположен-ные в лексикографическом порядке. Следующие 16 столбцов определяют все 16 различных функ-ций от двух переменных: в столбце под символом ψi находятся 4 значения функции ψi на этих 4-ёх наборах. Эти столбцы также расположены в лексикографическом порядке, но не сверху-вниз, как в таблицах 1 и 2, а слева направо.
Многие из этих 16-и функций часто используются в качестве «элементарных» и имеют собствен-ные названия и обозначения. Часть этих названий уже использовалась в главе 1 для описания операций над высказываниями и их истинностными значениями. При замене F и T на 0 и 1 все 6 рассмотренных в разделе 1-2.1 операций перейдут в 6 функций, представленных в таблице 4. Естественно, что используются те же названия.
1. ψ 0(x 1, x 2) = 0 – константа 0;
2. ψ 15(x 1, x 2) = 1– константа 1;
3. ψ 3(x 1, x 2) = x 1 – функция, равная 1-му аргументу;
4. ψ 12(x 1, x 2) = Ø x 1 – отрицание x 1;
5. ψ 5(x 1, x 2) = x 2 – функция, равная 2-му аргументу;
6. ψ 10(x 1, x 2) = Ø x 2 – отрицание x 2;
7. ψ 1(x 1, x 2) = x 1Ù x 2 – конъюнкция x 1 и x 2 (обозначается также через x 1& x 2 и x 1 x 2);
8. ψ 7(x 1, x 2) = x 1Ú x 2 – дизъюнкция x 1 и x 2;
9. ψ 13(x 1, x 2) = x 1 → x 2 – импликация x 1 и x 2 (читается «х 1 влечёт х 2» или «из х 1 следет х 2»;
10. ψ 6(x 1, x 2) = x 1 Å x 2 – сложение по модулю 2или разделительная дизъюнкция (исполь-зуется также обозначение x 1 + x 2);
11. ψ 9(x 1, x 2) = x 1 x 2 – эквивалентность x 1 и x 2 (читается как «x 1 эквивалентно x 2» или «x 2 = 1 тогда и только тогда, когда x 1 = 1»);
12. ψ 14(x 1, x 2) = x 1 | x 2 – штрих Шеффера(отрицание конъюнкции –«антиконъюнкция»);
13. ψ 8(x 1, x 2) = x 1 ↓ x 2 – стрелка Пирса(отрицание дизъюнкции –«антидизъюнкция»).
Заметим, что для 2-местных функций из этого списка в правых частях равенств использованы не только собственные имена, но и инфиксная запись,в которой значок операции помещается между 1-ым и 2-ым аргументами (запись вида ψ (x 1, x 2) называется префиксной). Функции ψ 2(x 1, x 2), ψ 4(x 1, x 2), ψ 11(x 1, x 2) не имеют специальных названий.
Пример 1. Таблица 4 задаёт все функции от двух переменных. Приведём в качестве примера использования этой таблицы несколько тождеств для булевых функций, в верности которых легко убедиться проверкой значений функций на всех четырёх наборах – 00, 01, 10 и 11 – значений двух переменных. Под тождествами здесь и далее понимаются равенства функций при всех наборах значений их переменных.
a → b º Ø a Ú b (2)
a Å b º (Ø a Ù b) Ú (a Ù Ø b) (3)
a Å 1 º Ø a (4)
a b º (a Ù b) Ú (Ø a Ù Ø b) (5)
a | b º Ø(a Ù b) (6)
a ↓ b º Ø(a Ú b). (7)
Использование других имён переменных вместо x 1, x 2 и x подчёркивает независимость свойств функций и связей между ними от этих имён, что, впрочем, совершенно естественно для всех разделов математики ■
Отметим, что функции ψ 3(x 1, x 2), ψ 12(x 1, x 2), ψ 5(x 1, x 2), ψ 10(x 1, x 2) зависят только от одной переменной, так что в ψ 3(x 1, x 2) и ψ 12(x 1, x 2) несущественной является переменная x 2, в ψ 5(x 1, x 2) и ψ 1(x 1, x 2) несущественной является переменная x 1. Функции ψ 0(x 1, x 2) и ψ 15(x 1, x 2) являются константами 0 и 1, т.е. в них обе переменные несущественны. Конъюнкция называется также логическим умножением, а дизъюнкция – логическим сложением.
Для удобства дальнейшего использования перепишем таблицу 4 ещё раз, заменив в ней нейтральные обозначения ψi на принятые значки для соответствующих функций:
Таблица 5. Булевы функции от 2-ух переменных со значками функций
| x 1 | x 2 | x 1Ù x 2 | ψ 2 | x 1 | ψ 4 | x 2 | x 1Å x 2 | x 1Ú x 2 | x 1 ↓ x 2 | x 1  x 2
| Ø x 2 | ψ 11 | Ø x 1 | x 1→ x 2 | x 1 | x 2 | ||
Понятие несущественных переменных позволяет дать несколько непривычное, но очень удобное определение равенства функций. Именно, две булевы функции f 1 и f 2 называются рав-ными, если функцию f 2 можно получить из функции f 1 путём добавления и ⁄ или удаления несу-щественных переменных. В частности, это позволяет считать, что во всяком конечном множес-тве функций все функции зависят от одного и того же множества переменных.
Разумеется, эти понятия относятся не только к булевым, но и к произвольным функциям. Хорошо известным примером является равенство sin2 x + cos2 x = 1, означающее, что переменная x в функции f (x) = sin2 x + cos2 x несущественна.
Функции и формулы
Табличное представления булевых функций подходят лишь для функций с небольшим числом аргументов. Формулы позволяют удобно представлять многие функции от бóльшего числа аргументов и оперировать различными представлениями одной и той же функции. Пусть B– некоторое (конечное или бесконечное) множество булевых функций. Зафиксируем некото-рое счётное множество переменных V = { x 1, x 2, …}. Определим по индукции множество формул над B с переменными из V. Одновременно будем определять числовую характеристику dep (Ф) формулы Ф, называемую её глубиной, и множество её подформул.
а) Базис индукции. Каждая переменная xi V и каждая константа c B является форму-лой гл-бины0,т.е. dep (xi) = dep (c)= 0. Множество её подформул состоит из неё самой. Напом-ним, что константа является функцией, все переменные которой несущественны, и c {0, 1}.
б) Шаг индукции. Пусть f (x 1, …, xm) B, Ф 1, …, Фт – формулы, и 
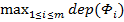= k. Тогда выражение Ф = f (Ф 1, …, Фm) является формулой, её глубина dep (Ф) равна k + 1, амножество подформул Ф включает саму формулу Ф и все подформулы формул Ф 1, …, Фт.
Понятие «доказательства по индукции», может быть, встречалось читателю. Но вот «опре-деления по индукции», чаще называемые индуктивными или рекурсивными определениями, для большинства читателей являются новыми. Остановимся на этом подробнее.
Речь идёт о задании, построении или описании множеств – в данном случае множества формул – некоторым процессом, который обычно называется порождающей процедурой (см. раздел 2-1). Идея такой процедуры состоит в определении некоторого достаточно простого исходного множества (это и есть базис индукции) и затем в последовательном добавлении в рассматриваемое множество новых элементов, полученных из уже имеющихся элементов, либо из каких-либо других объектов. Точная формулировка этих понятий далеко выходит за рамки настоящего пособия. Здесь мы просто проиллюстрируем «работу» порождающей процедуры на примере.
Пример 2. Определение множества формул над множеством функций B, состоящем из четырёх функций: константы 0, константы 1, Ø (отрицания) и Ú (дизъюнкции).
Сначала определяется исходное множество формул: {0, 1, x 1, x 2, …}. В соответствии с описанием базиса индукции, это множество объявляется множеством всех формул глубины 0. Далее, форму-лами глубины 1 являются все формулы вида Ø x 1, Ø x 2, …, а также формулы вида xi Ú xj (i, j = 1, 2, …) и вида c Ú xi, xi Ú c (i = 1, 2, …, c = 0, 1). Далее, формулами глубины 2 являются все формулы вида Ø xi Ú xj, xi ÚØ xj, Ø xi ÚØ xj, Ø(Ø xi), (xi Ú xj)Ú xk, и т.д.
Убедимся, например, что формулы Ø xi Ú xj и (xi Ú xj)Ú xk имеют глубину 2. По построению, подформулами формулы Ø xi Ú xj являются формулы Ф 1 = Ø xi и Ф 2 = xj. Формула Ф 1 имеет глубину 1, формула Ф 2 имеет глубину 0, максимальное из этих чисел равно 1 и по описанию шага индукции глу-бина формулы Ф = Ø xi Ú xj равна 1 + 1 = 2. В формуле (xi Ú xj)Ú xk Ф 1 = xi Ú xj, Ф 1 = xk, их глубина равна 1 и 0 и, значит, глубина Ф = (xi Ú xj)Ú xk равна 2. Заметим, что глубина формулы Ø xi ÚØ xj также равна 2 ■
Указанная конструкция определяет только «внешний» вид выражений, являющихся формула-ми, или их синтаксис. Для сопоставления каждой корректно построенной формуле определяемой ею булевой функции, т.е. для определения семантики формул, нам понадобится ещё одна индук-тивная процедура, в большой степени аналогичная уже рассмотренной.
Базис индукции. Пусть dep (Ф) = 0. Тогда Ф = xi V или Ф = c B. В 1-ом случае Ф опре-деляет функцию fФ (xi) = xi, во 2-ом – функцию, тождественно равную константе c.
Шаг индукции. Предположим (по индукции), что всем формулам над B глубины не бо-лее k булевы функции уже сопоставлены. Пусть Ф (x 1, …, xn) – произвольная формула глубины k + 1. По процедуре построения формул это означает, что Ф = f (Ф 1, …, Фm), где f (x 1, …, xm) B и при этом 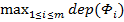= k. По предположению индукции, всем формулам глубины не более k уже сопоставлены булевы функции g 1(x 1, …, xn), …, gm (x 1, …, xn). Тогда формула Ф определяет функцию fФ (x 1, …, xn) = f (g 1, …, gm). Для полной аккуратности конструкции надо включить в индуктивное предположение очевидное условие, что формулы с переменными x 1, …, xn определяют функции от этих же переменных.
