В дальнейших разделах пособия оказывается достаточным интуитивного понятия функ-ции, представляемой стандартной записью (1). Проведённые рассуждения лишь демонстриру-ют возможность аккуратного определения понятия функции, основывающегося только на ба-зисных понятиях высказывания, множества и кортежа, без привлечения таких трудно форму-лируемых и нечётких понятиях, как независимая и зависимая переменная величина, измене-ние, закон, правило, и т.д.
Высказывательные формы
Высказывательные формы были определены в предыдущем разделе как формы, которые обозначают высказывания, т.е. являются высказываниями. Например, выражение
A 
(x > 3)
естественно считать двухместной высказывательной формой с высказывательной переменной A и числовой переменной x. Для случаев (которые нельзя априори исключать), когда на некото-рых наборах значений переменных высказывательная форма неопределенна, доопределим её логическим значением «Ложь» (т.е. значением F из двухэлементногомножества { T, F }). Поэто-му далее рассматриваются только всюду определённые высказывательные формы. Введённые в разделе 1-2.1 операции над высказываниями очевидным образом можно рассматривать и как операции над высказывательными формами. Для любых высказывательных форм 
и 
и без специальных пояснений ясен смысл форм: Ø , 
, 
, → 
, 
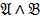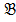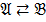, Å .
Пусть (x 1, …, xs) – s -местная (s ≥l) высказывательная форма, где x 1, …, xs – переменные формы , выписанные в каком-нибудь порядке. Пусть областью определения переменной xi бу-дет множество Мi (i = 1, …, s). Тогда областью истинности высказывательной формы назы-
| вается и как |
| или | (x 1, …, xs)
| обозначается множество тех кортежей á a 1, a 2,..., as ñ, для ко- |
торых (a 1, …, as) истинно.
Понятие области истинности позволяет связать операции над множествами с операциями над высказывательными формами. Так, очевидно, при s ≥ 1
(x 1, …, xs)  (x 1, …, xs)
| = | (x 1, …, xs)
| 
| (x 1, …, xs),
|
(x 1, …, xs)  (x 1, …, xs)
| = | (x 1, …, xs)
| 
| (x 1, …, xs).
|
Если Мi – обласги значений переменных xi (i = 1, …, s), то
| Ø (x 1, …, xs)
| = 
| (x 1, …, xs)).
|
2.1. Высказывательные формы и разрешающие процедуры. Вернёмся к вопросу о раз-решающей процедуре задания множеств, упомянутому в разделе 2-1. Суть дела состоит в опи-сании характеристических свойств его элементов и проверке этих свойств. Такая проверка и оп-ределяет «разрешение» для данного элемента принадлежать рассматриваемому множеству. В примерах 3-8, 3-9, 3-15 и 3-16 именно так задавались бесконечные графики. Теперь можно дать более детальное описание этого способа задания множеств. Именно, во многих случаях описы-ваемое множество естественно совпадают с областью истинности некоторой высказывательной формы. В примере 3-8 рассматривалось множество М точек á x, y ñ на плоскости, удовлетворяю-щих условию x 2 +y 2 = 1 (т.е. М – это окружность единичного радиуса с центром в начале коор-динат). Определим высказывательную форму (x, y): x 2 + y 2 = 1. Понятно, что рассматриваемое множество М совпадает с областью истинности данной высказывательной формы. В пункте 5) примера 1 высказывательная форма (x): x > 3 определяет бесконечное множество чисел, бóль-ших 3.
Вообще, в тех случаях, когда интересующее нас множество М совпадает с областью ис-тинности некоторой высказывательной формы , это множество М именно так и может быть задано. Для этого используется стандартное обозначение
М = { x | (x)}, (3)
которое читается так: М – это множество элементов x, для которых высказывательная форма истинна. В формуле (3) x = á x 1, x 2,..., xs ñ– это набор переменных данной высказывательной фор-мы. Более сложные вопросы проверки истинности произвольной высказывательной формы, приводящие, в частности, к формальному определению одного важного класса высказыватель-ных форм – предикатов – здесь не рассматриваются.
Кванторы
Рассмогрим две операции, применяемые только к высказывательным формам. Эти опера-ции, гак называемые навешивания кванторов, будучи применёнными к высказывательной форме, приводят либо снова к высказывательной форме, либо к высказыванию.
Начнем с простейшего случая. Пусть (х) – одноместная высказывательная форма; об-ласть значений переменной х обозначим буквой M. Обозначим через
(
х 
M) 
(х), (4)
или, если М ясно из контекста, через
( х) (х), (5)
следующее высказывание: «для любого значения переменной х высказывание, полученное под-становкой этого значения в форму (х) вместо х, истинно». Знак называется квантором общ-ности, переход от формы (х) к высказываниям (4), (5) – навешиванием на форму (х) кванто-ра общности по переменной х.
Обозначим через
(
х M) (х), (6)
или, если М ясно из контекста, через
( х) (х), (7)
следующее высказывание: «существует такое значение переменной х, что высказывание, полу-ченное подстановкой этого значения в форму (х) вместо х, истинно». Знак называется кван-тором существования, переход от формы (х) к высказываниям (6), (7) – навешиванием на форму квантора существования по переменной х.
Пример 12. Рассмотрим следующую высказывательную форму (х): «Девочку в группе зовут Маша» с одной переменной «девочка». Областью значений переменной является множес-тво всех девочек из данной группы. Используя кванторы, получаем высказывания (не высказы-вательные формы!):
«Всех девочек в группе зовут Маша»
«Некоторую девочку в группе зовут Маша»
«Ни одну девочку не зовут Маша», и т.п ■
Рассмотрим общий случай. Пусть (x 1, …, xs) – s-местная высказывательная форма (s ≥ 2); область значений переменной xi – множество Мi (i = 1, …, s). В силу введённых выше обозначе-ний для любого i = 1, …, s выражения
( хi M) (x 1, …, xs), (8)
( хi M) (x 1, …, xs) (9)
являются (s –1)-местными высказывательными формами, зависящими от переменных x 1, …, x i–1,
xi +1, …, xs. Буква xi в выражениях (8), (9) называется связанной переменной, а все остальные пе-ременные, на которые не навешаны кванторы, называются в таких случаях свободными пере-менными. Сразу скажем, что свободные переменные – это просто переменные в смысле опре-деления из раздела 1. А связанные переменные переменными в этом смысле (т.е. буквами, вмес-то которых можно подставлять элементы из множества значений) вообще не являются. Всё, что можно с ними сделать: заменить букву, написанную сразу после квантора, и все вхождения этой буквы в рассматриваемую форму, на одну и ту же букву, отличную от имён всех осталь-ных переменных. Заметим, что близкий смысл имеет индекс суммирования i в суммах вида 
, переменная интегрирования t в интегралах 
, переменная, по которой берётся максимум (или минимум): 
, и т.д. Общими во всех этих случаях являются два факта: 1) результат (сумма, интеграл, максимум и пр.) не зависит от этой связанной переменной, и 2) эту букву можно везде заменить на любую другую, не совпадающую с другими в данном выра-жении. Таким образом, можно сказать, что навешивание квантора по переменной х связывает эту переменную.
По определению квантора общности, высказывание
( хi M) (a 1, …, ai –1, xi, ai +1, …, as), (10)
истинно тогда и только тогда, когда для любого значения ai Mi переменной xi высказывание
(a 1, …, ai –1, ai, ai +1, …, as) (11)
истинно.
По определению квантора существования высказывание
( хi M) (a 1, …, ai –1, xi, ai +1, …, as), (12)
истинно тогда и только тогда, когда существует такое значение ai Mi переменной xi, что вы-сказывание
(a 1, …, ai –1, ai, ai +1, …, as) (13)
истинно.
С помощью кванторов можно ввести некоторые понятия, относящиеся к произвольным соответствиям (см. раздел 3-5). Пусть Г = á G, X, Y ñ– соответствие, А – множество. Образом А относительно Г называется и через Г (А) обозначается множество всех тех элементов из Y, каждый из которых соответствует в соответствии Г какому-нибудь элементу множества А. Таким образом,
Г (А) = { y Î Y | ( x Î А) á x, y ñÎ G }. (14a)
В формуле (14a) выражение после знака | имеет такой же смысл, как в формуле (3). Оно являет-ся одноместной высказывательной формой, зависящей от переменной y с областью значений Y. В множество Г (А) входят все те элементы Y, для которых высказывательная форма ( x Î А)á x, y ñÎ G истинна.
Если Г = á G, X, Y ñ– соответствие, А – множество, то полным прообразом А относитель-но Г называется и через Г –1(А) обозначается множество всех тех элементов из X, каждому из ко-торых соответствует в соответствии Г элемент множества А. Таким образом,
Г –1(А) = { x Î X | ( y Î А) á x, y ñÎ G }. (14b)
3.1. Отрицание высказываний с кванторами. Как и для любых высказываний, отрица-ние высказывательных форм, содержащих кванторы, является высказывательной формой или высказыванием с противоположным значением истинности. Если в высказывательной форме имеется ровно одна переменная, то после навешивания на неё кванторов (общности или сущес-твования) эта форма становится высказыванием – именно, высказыванием, содержащим кван-тор. Именно такие высказывания рассматриваются в данном разделе.
Пример 13. Вернёмся к 1-ому из высказываний из примера 12: «Всех девочек в группе зовут Маша». Отрицанием этого высказывания является высказывание «Некоторых девочек в группе не зовут Маша». Как обычно, то же самое утверждение может быть выражено различны-ми способами:
«Не всех девочек в группе зовут Маша»
«Неверно, что всех девочек в группе зовут Маша»
«По крайней мере одну девочку в группе не зовут Маша», и т.д ■
Пример 14. Рассмотрим высказывание «У некоторых кошек есть блохи». Поскольку «не-которые» в данном контексте значит «по меньшей мере, одна», высказывание «У некоторых ко-шек есть блохи» по смыслу совпадает с высказыванием «По меньшей мере, у одной кошки есть блохи». Отрицанием этого высказывания является «Ни у одной кошки нет блох», которое мо-жет быть записано также в виде «У всех кошек нет блох» ■
Обобщая рассуждения из примеров 13 и 14, можно прийти к следующей таблице, содер-жащей схемы для построения отрицаний высказываний с кванторами.
Таблица 1. Отрицания высказываний с кванторами
| Высказывание | Отрицание |
| Все делают (имеют и пр.) | Некоторые не делают (Эквивалентно: не все делают) |
| Некоторые дела-ют (имеют и пр.) | Никто не делает (Эквивалентно: все не делают) |
Отрицанием отрицания является само исходное высказывание. Как и все остальные высказыва-ния, они могут быть записаны в разном виде (см. таблицу 1).
Пример 15. Рассмотрим следующие изображения, разделённые на группы A, B, и C.
Отметим одной (или несколькими) буквами группу или группы картинок, удовлетворяющих условию «По меньшей мере хотя бы одна картинка из группы не имеет рамки». Группы A и B
удовлетворяют этому условию, а группа C – нет ■
Задания
Задание 1. См. пример 3 для образца. Для данной одноместной формы и данной области значений переменной х:
а) найти допустимые значения;
б) установить, является ли форма всюду определённой;
в) установить, является ли форма нигде не определённой;
г) установить, является ли форма числовой.
1. Форма 1 ∕ x, область значений {3, 5, 0}
2. Форма 1 ∕ x, область значений {3, 5}
3. Форма 1 ∕ x, область значений {0}
4. Форма 1 ∕ x, область значений { 
, +}
5. Форма 
, область значений {–5,–4,–3, –2,–1, 0, 1, 2, 3, 4}
6. Форма , область значений {–5,4}
7. Форма , область значений {3,–4}
8. Форма , область значений {–8, 7, 100}
9. Форма , область значений {3,–4,!}
10. Форма , область значений {3, 1+ i }■
Задание 2. Для данных высказывательных форм найти области истинности.
1. (x, y): x 2 + y 2 ≥ 2 xy
2. (x, y): x + y ≥ 2 xy
3. 
(x, n): xn > 1 + n (x – 1)
4. (x, y) → (x, y)
5. 
(x, n): x < n
6. (x, n) 
(x, n) ■
Задание 3. Нарисовать на координатной плоскости область истинности высказывательной формы (x, y) с числовыми переменными x, y, если
1. (x, y): y = x 2.
2. (x, y): 2 x + 3 y – 1 > 0.
3. (x, y): sin(x + y) = 0.
4. (x, y): y = x 2 + 1 ∕ x.
5. (x, y): y < x 2 + 1 ∕ x.
6. (x, y): y = 
.
7. (x, y): y = 
■
Задание 4. Проверить следующие равносильности
1. ( х)[ (х) (x)] º ( х) (х) ( х) (x)
2. ( х)[ (х) (x)] º ( х) (х) 
( х) (x)
3. ( х)[ (х) (x)] º ( х) (х) ( х) (x)
4. ( х)[ (х) (x)] º ( х) (х) ( х) (x)
5. ( х)[ (х)→ (x)] º ( х) (х)→( х) (x)
6. ( х)[ (х) 
(x)] º ( х) (х) 
( х) (x)
