Выражения, переменные и формы 4 страница

Заметим, что разделение конструкций на синтаксическую и семантическую части доста-точно естественно для дискретной математики. Примерно по такой же схеме (но заметно слож-нее) выглядит определение предикатов (здесь не рассматривается).

Далее будут рассматриваться формулы над множествами функций от одной и двух пере-менных, которые являются подмножествами одного множества так называемых элементарных функций B _e = {0, 1, Ø, Ù, Ú, →, Å, , |, ↓} (см. раздел 1.1). Определение формул в этих бази-сах и сопоставляемых им функций является частным случаем рассмотренных выше общих конструкций.

Пример 3. Для определения функции, задаваемой (говорят также реализуемой) форму-лой, удобно использовать таблицу, строки которой соответствуют наборам значений перемен-ных, а в столбцах под знаком каждой операции стоят значения функции, реализуемой соответс-твующей подформулой. Для формулы Ф (x ₁, x ₂, x ₃) = (x ₁Ú x ₂) → (x ₃ (x ₁ ↓ Ø x ₂)) функция f_Ф опре-деляется в последнем столбце следующей таблицы 6:

Таблица 6. Построение таблицы истинности для функции f_Ф = (x ₁Ú x ₂) → (x ₃ (x ₁ ↓ Ø x ₂))

x 1	x 2	x 3	1) x 1Ú x 2	2) Ø x 2	3) x 1↓2	4) x 3 3	5) 1→4

Заголовок x ₁Ú x ₂ столбца 1) и заголовок Ø x ₂ столбца 2) понятны – в эти столбцы заносятся ре-зультаты указанных действий. Заголовок x ₁↓2 столбца 3) означает стрелку Пирса, применённую к x ₁ и функции, уже подсчитанной в столбце 2). Заголовок x ₃ 3 столбца 4) означает эквивалент-ность, применённую к x ₃ и функции, уже подсчитанной в столбце 3). Заголовок 1→4 столбца 5) означает импликацию, посылка которой уже подсчитана в столбце 1), а заключение – в столбце 4). Таблицы, помогающие аналогичным образом вычислять булевы функции от двух-четырёх переменных по заданным формулам, называются таблицами истинности ■

Укажем на различие между таблицами 6 и 2. В таблице 2 в последнем столбце значения функции на всех наборах задавались, а понятие формулы не использовалось. В то же время в таблице 6 функция задаётся формулой, а заголовки столбцов подробно указывает на процесс вычисления булевой функции, реализуемой данной формулой.

2.1. Равносильность булевых формул. Булевы формулы Ф и Ψ называются равносиль-ными, если соответствующие им функции f_Ф и f_Ψ равны. Равносильность двух формул обозна-чается как Ф º Ψ. Равносильные формулы называют также тождественно равными, а выраже-ния вида Ф º Ψ – логическими тождествами. Вместо термина «равносильность» иногда ис-пользуется термин «эквивалентность».

Таким образом, равносильные формулы реализуют одну и ту же булеву функцию. Ниже при-водится ряд пар равносильных формул (тождеств), отражающих существенные свойства логичес-ких операций и важные соотношения между различными операциями. Они часто позволяют нахо-дить для булевых функций по реализующим их формулам более простые эквивалентные формулы. Большинство из приводимых тождеств имеют собственные имена. Часто их называют законами логики.

Пусть ○ – это одна из функций Ù, Ú, Å. Для этих трёх функций выполнены следующие две равносильности (законы ассоциативности и коммутативности).

1) Закон ассоциативность: (a ○ b ₂) ○ c º a ○ (b ₂ ○ c).

Законы ассоциативности показывают, что значения формул, составленных из переменных и одних операций конъюнкции, одних операций дизъюнкции, одних операций сложения по моду-лю 2 не зависят от расстановки скобок. Поэтому вместо формул (a ○ x ₂) ○ c и a ○ (b ○ c) мы бу-дем для упрощения писать выражение a ○ b ○ c, которое не является формулой непосредственно по определению, но может быть легко превращено в неё с помощью расстановки скобок.

2) Закон коммутативность: a ○ b º b ○ a

3) Законы дистрибутивные:

(a Ú b) Ù c º (a Ù c) Ú (b Ù c)

(a Ù b) Ú c º (a Ú c) Ù (b Ú c)

(a Å b) Ù c º (a Ù c) Å (b Ù c)

4) Закон двойного отрицания: Ø(Ø a) º a

5) 3аконы де Моргана (внесение отрицания внутрь скобок):

Ø (a Ú b) º Ø a Ù Ø b

Ø (a Ù b) º Ø a Ú Ø b

6) Законы упрощения:

законы идемпотентности a º a, a Ú a º a

закон противоречия a ÙØ a º 0; закон исключенного третьего a ÚØ a º 1

законы 0 и 1 a Ù0 º 0, a Ú 0 º a, a Ù1 º a, 1 º 1

7) Правила поглощения: a Ú ab º a; a (a Ú b) º a

8) Правило склеивания: a b Ú a (Ø b) º a

9) Правило вычёркивания: a b Ú Ø a º b Ú Ø a

Далее будем часто писать ab вместо a Ù b. Эта «вольность записи» общепринята, так как она приводит к заметному сокращению формул, а «оправдывается» тем, что результаты опера-ции конъюнкции 0Ù0 = 0Ù1 = 1Ù0 = 0, 1Ù1 = 1 полностью совпадает с таблицей умножения чисел 0 и 1. При отсутствии скобок знак отрицания, стоящий перед переменной, имеет самый высокий приоритет, т.е. операция отрицания выполняется прежде всего. Следующий приоритет имеет логическое умножение. Остальные операции выполняются в порядке, указанном скобка-ми.

Обратим также внимание на следующее. Все приведённые законы и правила – это не зако-ны природы. Они доказываются (точнее, проверяются) подстановкой в левую и правую части логических тождеств всех наборов значений переменных (при n = 2 – четырёх наборов, при n = 3 – восьми).

Пример 4. Проверим справедливость 2-го закона дистрибутивности

(a Ù b) Ú c º (a ₁ Ú c) Ù (b Ú c)

Для левой и правой частей проверяемого тождества получаем две таблицы истинности (см. для сравнения таблицу 5):

Таблица 7а. Левая часть тождества a 1 b c 1) a 1Ù b 2)1Ú c

Таблица 7б. Правая часть тождества a 1 b c 1) a 1Ú c 2) b Ú c 3) 1Ù2

Поскольку правые столбцы полностью совпадают, то функция, реализуемая формулой из левой части, совпадает с функцией, реализуемой формулой из правой части. Это и означает справед-ливость 2-го закона дистрибутивности

Если в этом законе удалить знак конъюнкции (см. выше) и заменить дизъюнкцию на сло-жение, то данное тождество примет вид ab + c º (a + c)(b + c), что, разумеется, для чисел с опе-рациями умножения и сложения неверно. Заметим, что при такой же замене в 1-ом законе дистрибутивности получаем закон, очевидно выполняющийся для чисел (и даже матриц): (a + b) c º ac + bc, что ещё раз говорит об аккуратности при использовании аналогий между буле-выми и числовыми формулами ■

Многие из приведённых тождеств (2) – (7) и 1) – 9) можно не проверять, а выводить из других тождеств. Но на этом мы останавливаться не будем, стремясь к максимально возможной стандартизации рассуждений (для чего на самом деле и разрабатывалась булева алгебра ещё в 19-ом веке). Заметим, что все тождества остаются в силе, если вместо переменных a, b, c под-ставлять произвольные формулы в любом базисе.

Из определения равносильности формул непосредственно следует так называемый прин-цип замены равносильных подформул: пусть формула α является подформулой формулы Ф, формула α' равносильна α и формула Ф' получена из Ф посредством замены некоторого вхож-дения α на α'. Тогда Ф' равносильна Ф, т.е. Ф ' º Ф.

Применяя этот принцип и используя основные тождества, можно находить для заданной формулы другие равносильные ей формулы.

Пример 5. Упрощение формулы. Имеет место цепочка тождеств, устанавливающая рав-носильность всех входящих в неё формул:

((x ₁→ x ₂) x ₁ÚØ x ₁ x ₂)(x ₁ÚØ x ₂) º ((Ø x ₁Ú x ₂) x ₁ÚØ x ₁ x ₂)(x ₁ÚØ x ₂) º (Ø x ₁ x ₁Ú x ₁ x ₂ÚØ x ₁ x ₂)(x ₁ÚØ x ₂) º

(x ₁ x ₂ÚØ x ₁ x ₂)(x ₁ÚØ x ₂) º x ₂(x ₁ÚØ x ₂) º x ₁ x ₂.

Дадим пояснения. В исходной формуле заменяем подформулу x ₁→ x ₂ на равносильную в силу формулы (2) подформулу Ø x ₁Ú x ₂. Получаем формулу, стоящую справа от 1-го знака º. Да-лее, заменяя в ней по 1-му закону дистрибутивности 3) формулу (Ø x ₁Ú x ₂) x ₁ на Ø x ₁ x ₁Ú x ₁ x ₂, полу-чаем формулу, стоящую справа от 2-го знака º. Далее, используя в формуле Ø x ₁ x ₁ закон проти-воречия, получаем Ø x ₁ x ₁ º 0, откуда в силу закона нуля x Ú 0 º x выводим, что Ø x ₁ x ₁Ú x ₁ x ₂ÚØ x ₁ x ₂ º x ₁ x ₂ÚØ x ₁ x ₂, и получаем формулу справа от 3-го знака º. Далее, по правилу склеивания, заме-няем подформулу x ₁ x ₂ÚØ x ₁ x ₂ на x ₂ и приходим к формуле справа от 4-го знака º. Пользуясь ещё раз дистрибутивностью и законом противоречия, заменяем x ₂(x ₁ÚØ x ₂) на окончательную прос-тую формулу x ₁ x ₂, равносильную исходной формуле ((x ₁→ x ₂) x ₁ÚØ x ₁ x ₂)(x ₁ÚØ x ₂) ■

Как уже говорилось, закон ассоциативности позволяет рассматривать многоместную конъюнкцию и многоместную дизъюнкцию 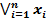в качестве формул. В случае n = 1 обе формулы означают х ₁. Пустая конъюнкция (при п = 0) полагается равной 1, пустая дизъюн-кция – равной 0.

Законы де Моргана 5) могут быть обобщены для произвольного неотрицательного n:

Ø(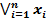) º (8а)

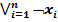Ø() º (8б)

При п > 2 в этом можно убедиться, представив многоместную функцию расстановкой скобок с помощью двуместных. При п = 3, например, цепочка преобразований для (8б) имеет вид:

Ø(x ₁ Ù x ₂ Ù x ₃) = Ø((x ₁ Ù x ₂) Ù x ₃) = Ø(x ₁ Ù x ₂) Ú Ø x ₃) = (Ø x ₁ Ú Ø x ₂) Ú Ø x ₃ = Ø x ₁ Ú Ø x ₂ Ú Ø x ₃.

В случае п = 0 и п = 1 соотношения (8) выполняются очевидным образом.

Соотношения (8) допускают дальнейшее обобщение. Пусть функция f реализуется некото-рой формулой в базисе B = {0, 1, Ø, Ù, Ú}. Тогда формула, реализующая её отрицание Ø f,может быть получена по следующему алгоритму.

Алгоритм отрицания в базисе {0, 1, Ø, Ù, Ú}.

1. Все конъюнкции (значки Ù) должны быть заменены на дизъюнкции (значки Ú) и наоборот, все дизъюнкции должны быть заменены на конъюнкции.

2. Переменные x_i должны быть заменены на их отрицания Ø x_i.

3. Константы 0 и 1 должны быть заменены противоположными константами 1 и 0 ■

Обоснованием алгоритма являются законы де Моргана. Приведём пример, иллюстрирую-щий работу алгоритма отрицания.

Пример 6. Пусть функция f задается формулой (x ₁Ù x ₂)Ú(Ø x ₁ÙØ x ₂) º x ₁ x ₂ (см. тождество (5)). При отрицании левой части предполагаемого тождества получаем

Ø((x ₁Ù x ₂)Ú(Ø x ₁ÙØ x ₂)) º Ø(x ₁Ú x ₂)ÙØ (Ø x ₁ÙØ x ₂) º (Ø x ₁ÙØ x ₂) Ù (Ø(Ø x ₁)ÚØ(Ø x ₂)) º (Ø x ₁Ù Ø x ₂)Ù(x ₁Ú

x ₂) º (Ø x ₁Ù x ₁ÚØ x ₂Ù x ₁ÚØ x ₁Ù x ₂ÚØ x ₂Ù x ₂ º Ø x ₂Ù x ₁ÚØ x ₁Ù x ₂ º Ø x ₁Ù x ₂ Ú x ₁ÙØ x ₂ º x ₁ Å x ₂. (9)

1-ое тождество следует из 2-го закон де Моргана. 2-ое тождество получено применением законов де Моргана к обоим слагаемым дизъюнкции. 3-ье тождество получено применением закона двойного отрицания к выражениям Ø(Ø x ₁) и Ø(Ø x ₂). Далее последовательно использова-на дистрибутивность для 4-го тождества, закон исключённого третьего для 5-го тождества (два члена из четырёх пропадают), коммутативность в 6-ом тождестве и тождество (3) в последнем, 7-ом тождестве. Преобразования заканчиваются формулой x ₁ Å x ₂. Таблица 5 подтверждает, что функции x ₁ x ₂ и x ₁ Å x ₂ (т.е. эквивалентность и сложение по модулю 2) действительно являются отрицаниями друг друга, поскольку на любом наборе, где одна из них равна 1, другая равна 0, и наоборот ■

2.2. СДНФ и СКНФ. Всякая булева функция от n переменных, по определению, задаётся своими значениями на 2 ⁿ наборах нулей и единиц. Однако уже при сравнительно небольших значениях n задание функции таблицей громоздко и неудобно. Поэтому желательно иметь не-который регулярный способ представления булевых функций при помощи формул, которые (в отличие от таблиц) могут быть преобразованы, упрощены и т.д. В настоящем разделе даются наиболее известные представления булевых формул в виде совершенной дизъюнктивной нор-мальной формы (СДНФ) и совершенной конъюнктивной нормальной формы (СКНФ).

Пусть σ {0, 1}. Положим

x^σ = . (10)

Сформулируем несколько почти очевидных утверждений, необходимых для определения СДНФ и СКНФ.

Утверждение 1. x^σ = 1 тогда и только тогда, когда x = ■

Утверждение 2. Конъюнкция … равна 1 на единственном наборе значений пе-ременных x ₁, …, x_k: x ₁ = σ ₁, …, x_k = σ _k ■

Следующее утверждение позволяет выразить функцию f (x ₁, …, x_n) через функции от мéньшего числа аргументов.

Утверждение 3. Всякая логическая функция f (x ₁, …, x_n) при любом k = 1, 2, …, n представляется в виде

f (x ₁, …, x_k, x_{k +1}, …, x_n) = 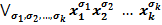f (σ ₁, …, σ_k, x_{k +1}, …, x_n), (11)

где дизъюнкция берётся по всем 2 ^k наборам σ ₁, …, σ_k значений 0 и 1.

Доказательство следует из того, что для любого набора α ₁, …, α_n левая и правая части (11) совпадают ■

Представление (11) произвольной булевой функции называется разложением по перемен-ным x ₁, …, x_k. Его частный случай при k = 1 имеет вид

f (x ₁, x ₂, …, x_n) = x ₁ f (1, x ₂, …, x_n) Ú Ø x ₁ f (0, x ₂, …, x_n) (12)

и носит название формулы разложения по одной переменной. Разумеется, вместо x ₁ можно взять любую другую переменную.

Воспользовавшись утверждением 3 при k = n, получаем представление

f (x ₁, …, x_n) = f (σ ₁, …, σ_n). (13)

При этом в правую часть (13) входят только те «слагаемые», на которых значения f (σ ₁, …, σ_n) равны 1. Опуская значения f (σ ₁, …, σ_n), поскольку логическое умножение» на 1 можно не пи-сать, получаем из (13) равенство

f (x ₁, …, x_n) = , (14)

где дизъюнкция берётся по всем наборам σ ₁, …, σ_n, на которых функция f (σ ₁, …, σ_n) = 1.

Представление (8) и называется совершенной дизъюнктивной нормальной формой (сок-ращённо СДНФ) булевой функции f от n переменных. С учетом соглашения о том, что пустая дизъюнкция равна 0, оно распространяется на функцию f (x ₁, …, x_n), тождественно равную 0.

СДНФ обладает следующими свойствами.

1. Она является дизъюнкцией некоторых конъюнкций К ₁ Ú К ₂ Ú … Ú К_s.

2. Каждая из конъюнкций К_i имеет вид , где n – число переменных функции.

3. Все конъюнкции К ₁, К ₂, …, К_s различны.

Утверждение 4а. Представление булевой функции, обладающее свойствами 1 – 3, единст-венно с точностью до перестановки конъюнкций ■

Введём в рассмотрение также важное для дальнейшего понятие дизъюнктивной нор-мальной формы (ДНФ). От СДНФ ДНФ отличается только одним: входящие в неё конъюнк-ции не обязаны включать все переменные. Например, формула xy Ú y Ø z является ДНФ, но не яв-ляется СДНФ. Однако СДНФ является частным случаем ДНФ.

Всякая функция f (x ₁, …, x_n) 1 может быть выражена также в виде конъюнкции некото-рых дизъюнкций …Ú . Чтобы получить это представление, выпишем СДНФ функ-ции Ø f (x ₁, …, x_n) 0:

Ø f (x ₁, …, x_n) = . (15)

Воспользовавшись алгоритмом отрицания из раздела 2.1 и тем, что Ø(Ø f) = f), из (9) получаем

f (x ₁, …, x_n) = (16)

(условие суммирования Ø f (x ₁, …, x_n) = 1 заменено на эквивалентное условие f (x ₁, …, x_n) = 0).

Представление (16) носит название совершенной конъюнктивной нормальной формы (сокращённо СКНФ). С учетом соглашения о том, что пустая конъюнкция равна 1, оно распрос-траняется на функцию f (x ₁, …, x_n), тождественно равную 1.

СКНФ обладает следующими свойствами.

1. Она является конъюнкцией некоторых дизъюнкций D ₁ Ù D ₂ Ù … Ù D_t.

2. Каждая из дизъюнкций D_i имеет вид , где n – число переменных функ-ции.

3. Все дизъюнкции D ₁, D ₂, …, D_s различны.

Утверждение 4б. Представление булевой функции, обладающее свойствами 1 – 3, единст-венно с точностью до перестановки дизъюнкций ■

Это утверждение может быть доказана непосредственно либо на основе утверждения для СДНФ, применённой к функции Ø f.

Понятие КНФ определяется аналогично понятию ДНФ.