2) угловая скорость w – векторная физическая величина, показывающая, как изменяется угол поворота Dj в единицу времени, численно равная первой производной от угла поворота по времени. Вектор угловой скорости направлен вдоль оси вращения в сторону, определяемую правилом правого винта:
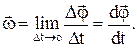
3) угловое ускорение e – векторная физическая величина, характеризующая изменение угловой скорости в единицу времени, численно равная первой производной от угловой скорости по времени или второй производной от угла поворота по времени Направление вектора углового ускорения совпадает с направлением вектора угловой скорости в случае ускоренного вращения и противоположно – в случае замедленного:
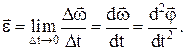
Период вращения (T) – время, в течение которого тело совершает один полный оборот.
Частота вращения (n) – число оборотов, совершаемых в единицу времени.
Круговая (циклическая) частота ω – число оборотов, совершаемых за время, равное 2π.
Связь между периодом, частотой и круговой частотой:
ω=2πn=2π/T; n=1/T.
Связь между линейными и угловыми скоростями и ускорениями:
Колебательные движения (колебания) – движения или процессы, обладающие повторяемостью во времени.
Гармонические колебания (простейший вид колебаний) – движения, при которых смещение материальной точки (тела) от положения равновесия изменяется по закону синуса или косинуса (рис. П 1. 5):
x=x0×sin(w0t+j0),
где x – смещение это удаление материальной точки от положения равновесия в данный момент времени t;
x0 – амплитуда колебаний это максимальное удаление материальной точки от положения равновесия;
(wt+j0) – фаза колебаний. Периодически изменяющийся аргумент функции, описывающей колебательный или волновой процесс. Определяет положение материальной точки в данный момент времени t;
j0 – начальная фаза колебаний. Определяет положение материальной точки в начальный момент времени t=0;
w=2p/T=2pn – круговая (циклическая) частота колебаний;
T – период колебаний;
n – частота колебаний.
Скорость при гармоническом колебательном движении (колебательная скорость) – физическая величина, которая показывает, как изменяется смещение в единицу времени, численно равная первой производной от смещения по времени:
.
Ускорение при гармоническом колебании – физическая величина, которая показывает, как изменяется скорость в единицу времени, численно равная первой производной от скорости или второй производной от смещения по времени:
.
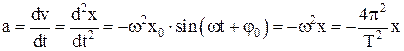Знак "минус" означает – ускорение направлено в сторону, противоположную смещению.
Сложение гармонических колебаний одного направления (рис. П 1. 6) с одинаковыми амплитудами и частотами (x01=x02; w1=w2=w), но разными начальными фазами (j02 ¹ j01), проводят аналитически. Уравнение результирующего колебания имеет вид
где 
– амплитуда результирующего колебания;
– фаза результирующего колебания.
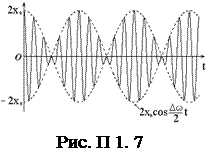Биения – возникают при сложение колебаний одного направления (рис. П 1. 7), с одинаковыми амплитудами (x02=x01), начальными фазами j01=j02=0 и круговыми частотами, мало отличающимися друг от друга (w1» w2). Уравнения таких колебаний имеют вид
x1=x01×sinw1t; x2=x01×sinw2t.
Уравнение результирующего колебания:
x=x1+x2=2x01× 
,
где 
– амплитуда результирующего колебания, которая зависит от Dw=w1 – w2 – разности частот складываемых колебаний;
– смещение результирующего колебания, изменяющееся по гармоническому закону;
Частота и период результирующего колебания:
Частота и период изменения амплитуды в этом случае:
Сложение взаимно перпендикулярных колебаний приводит к тому, что траектория движения представляет собой замкнутые фигуры, называемые фигурами Лиссажу (рис. П 1. 8):
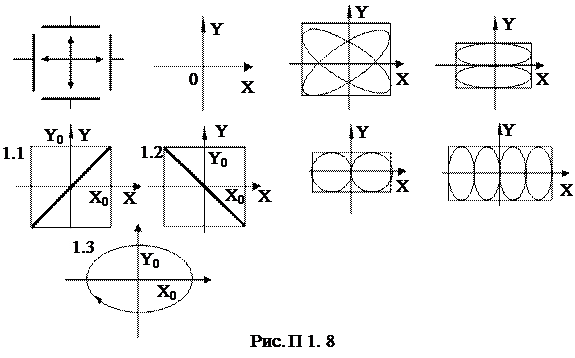
1) сложение колебаний с одинаковыми частотами (w1=w2=w), различными амплитудами (x0¹ y0) с начальными фазами j1=j2=0 – результирующее колебание – гармоническое. Траектория движения – прямая линия, уравнение которой имеет вид
y=(y0/x0)×x;
2) сложение колебаний, начальные фазы j1 и j2 которых отличаются на p/2 (j1 – j2=p/2) – результирующее колебание – гармоническое. Траектория движения – эллипс (при равных амплитудах x0=y0 – траектория результирующего движения – окружность) с полуосями, равными, x0 и y0, уравнение которого:
(y/y0)2+(x/x0)2=1;
3) сложение колебаний, периоды которых относятся как целые числа – через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка возвращается в начальное положение – получаются фигуры Лиссажу более сложной формы.
Динамика изучает движение и взаимодействия тел совместно с причинами, обусловливающими тот или иной характер движения и взаимодействия.
Основная задача динамики – для данного тела по известной силе найти его ускорение и, наоборот, по известному ускорению найти результирующую силу, действующую на тело.
Масса m – физическая величина, характеризующая количество вещества, инертность, гравитационные свойства и энергию материального тела. Массу тела, определяющую его инертные свойства, называют инертной массой.
Центр масс (или центр инерции) системы – воображаемая точка С, положение которой характеризует распределение массы этой системы и определяется радиус – вектором:
,
где mi и r i – соответственно масса и радиус – вектор i – й материальной точки;
n – число материальных точек в системе.
Скорость центра масс
,
где 
– полный импульс системы.
Импульс p ( количество движения) – физическая величина, описывающая свойства движущихся тел, равная произведению массы на скорость:
p=mv.
Полный импульс системы равен произведению массы системы на скорость ее центра масс:
p= m v c.
Покой – частный случай равномерного прямолинейного движения со скоростью v =0.
