Механика – раздел физики, в котором изучается механическое движение, причины, вызывающие это движение, и происходящие при этом взаимодействия между телами.
Механическое движение – изменение с течением времени взаимного положения тел или их частей (частиц) в пространстве.
Кинематика – раздел механики, в котором изучают геометрические свойства движения и взаимодействия тел в не связи с причинами их порождающими.
Физические модели (научные абстракции) классической механики:
1) материальная точка – протяженное тело, размерами которого в условиях данной задачи можно пренебречь, обладающее массой. Понятие применимо при поступательном движении или когда в изучаемом движении можно пренебречь вращением тела вокруг его центра масс;
2) абсолютно твердое тело – тело, расстояние между двумя любыми точками которого в процессе движения остается неизменным. Применимо, когда можно пренебречь деформацией тела;
3) сплошная изменяемая среда – понятие применимо при изучении движения изменяемой среды (деформируемого твердого тела, жидкости, газа), когда можно пренебречь молекулярной структурой среды.
Система единиц измерения физических величин – совокупность основных и производных эталонов. В настоящее время предпочтительной во всех областях науки и техники является система СИ.
В системе СИ единицами измерения являются: 1) основные – единица измерения длины (L) – 1 м; единица измерения массы (M) – 1 кг; единица измерения времени (T) – 1 с; единица измерения температуры (Т) – 1 К; единица измерения силы тока (I) – 1 А; единица измерения силы света (I) – 1 св.; 2) дополнительные – единица измерения плоского угла – 1 рад; единица измерения телесного угла – 1 стерад.
Тело отсчета – произвольно выбранное, условно неподвижное тело, по отношению к которому рассматривается движение данного тела.
Система отсчета – произвольная система координат, связанная с телом отсчета, например: а) прямоугольная, трехмерная система координат, в точке пересечения осей которой помещают тело отсчета; б) полярная система координат, положение материальной точки (тела) в которой задается радиус – вектором r и углами: j; q.
Траектория движения – совокупность последовательных положений материальной точки (тела) в процессе ее движения
Поступательное движение – движение, при котором тело перемещается параллельно самому себе. При этом все точки тела описывают одинаковые траектории, смещенные относительно друг друга.
Положение материальной точки (тела) в прямоугольной системе отсчета, в данный момент времени, может быть определено: с помощью координат x, y, z – M(x,y,z); с помощью радиус – вектора r и естественным (траекторным) способом (рис. П 1. 1).
Уравнения движения материальной точки (тела) в кинематике:
x=f1(t); y=f2(t); z=f3(t);
rx=f1(t); ry=f2 (t); rz=f3(t),
где x, y, z – координаты;
rx, ry, rz – проекции радиуса вектора r на соответствующие оси координат.
Основные понятия и определения кинематики материальной точки и твердого тела, движущегося поступательно:
1) перемещение (рис. П 1. 2) – вектор D r, проведенный из начального положения материальной точки (тела) в положение этой точки в данный момент времени (приращение радиус – вектора за рассматриваемый промежуток времени):
D r = r 1– r 2;
2) элементарное перемещение d r – бесконечно малое перемещение, которое с достаточной степенью точности совпадает с соответствующим участком траектории движения. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения численно равен пройденному пути:
½D r ½=DS;
3) путь – расстояние, пройденное телом при его движении по траектории. В частных случаях перемещение и путь могут совпадать;
4) мгновенная линейная скорость – векторная физическая величина, характеризующая состояние движения, показывающая, как изменяется перемещение в единицу времени, равная первой производной от перемещения по времени:
;
5) средняя скорость неравномерного движения – скалярная физическая величина, численно равная отношению всего пути, пройденного телом (материальной точкой), к тому промежутку времени, в течение которого совершалось движение:
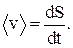
6) линейное ускорение – векторная физическая величина, характеризующая изменение скорости в единицу времени, равная первой производной от скорости или второй производной от перемещения по времени:
;
7) тангенциальное ускорение а t – составляющая ускорения, направленная вдоль касательной к траектории движения. Изменяет линейную скорость только по величине:
;
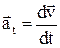8) нормальное ускорение a n – составляющая линейного ускорения, направленная по нормали n к вектору линейной скорости, т.е. к касательной в данной точке:
,
где R – радиус кривизны траектории движения;
n – единичный вектор нормали к траектории движения;
9) полное ускорение a:
.
10) среднее ускорение при неравномерном движении:
.
Принцип относительности Галилея (в классической механике) – никакие опыты, проводимые в инерциальных системах отсчета с механическими приборами, не позволяют установить, покоится система отсчета или движется равномерно и прямолинейно по отношению к другой инерциальной системе отсчета. Предполагается, что время не зависит от относительного движения систем отсчета.
Преобразования Галилея определяют положение произвольной материальной точки в двух инерциальных системах отсчета, одна из которых движется со скоростью v o относительно другой (при условии, если направление скорости v 0 совпадает с направлением r o):
r=r ' +r 0 =r ' +v ot; t=t'.
где r и r ' – радиус – векторы, определяющие положение материальной точки в неподвижной и подвижной системе отсчета в данный момент времени;
r o – радиус вектор, определяющий положение начала координат системы К' (подвижной) в системе К (неподвижной).
В проекциях на оси координат в произвольный момент времени t положение выбранной точки в системе К можно определить так:
x=x'+v0xt, x'=x – v0xt,
у=у'+v0уt, у'=у – v0уt,
z=z'+v0zt, z'=z – v0zt,
t=t'. t=t'.
Ковариантные или инвариантные уравнения – уравнения, обе части которых при переходе от одной системы координат к другой преобразуются одинаково и сохраняют свой вид во всех инерциальных системах отсчета.
Закон сложения скоростей в классической механике:
v = v '+ v 0.
Относительное расстояние между выбранными точками пространства в системах отсчета определяется соотношением – они абсолютны, т.е. инвариантны:
В подвижной
,
В неподвижной
.
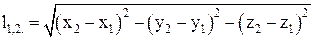Инварианты преобразований – инвариантные величины (расстояния между телами (точками), промежутки времени между событиями, относительные скорости тел, ускорения).
Вращательное движение твердого тела вокруг неподвижной оси – движение, при котором какие – либо две его точки остаются неподвижнымив процессе движения. Прямая, проходящая через эти точки, – ось вращения; все остальные точки твердого тела описывают окружности в плоскостях, перпендикулярных к оси вращения, центры которых лежат на этой оси (рис. П 1. 3).
Основные кинематические характеристики вращательного движения (рис. П 1. 4):
