C1: Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
|
Рисунок 2
На рисунке 2 точка А принадлежит плоскости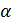 
, а точки B и С не принадлежат ей.
C2: Если две различные плоскости имеют общую точку, то они пересекаются по прямой.
Рисунок 3
На рисунке 3 две различные плоскости 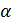и 
имеют общую точку А, а значит, по аксиоме С2существует прямая принадлежащая каждой из этих плоскостей. Приэтом если какая-либо точка принадлежит обеим плоскостям, то она принадлежит прямой а.
Плоскости 
и 
в этомслучае называются пересекающимися по прямой а.
C3: Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Рисунок 4
На рисунке 4 изображены две различные прямые a и b имеющие общую точку О, а значит, по аксиоме С3, существует плоскость 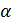, содержащая прямые a и b. При этом по той же аксиоме C3 плоскость 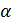единственная.
Пользуясь этими аксиомами, можно доказать несколько первых теорем стереометрии.
Теорема 1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
Теорема 2. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Теорема 3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Упражнения с решениями
Пример 1. Дана плоскость 
. Доказать, что существует прямая, не лежащая в плоскости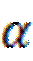 
и пересекающая ее.
Решение. Возьмем в плоскости точку А, что можно сделать по аксиоме С1. По той же аксиоме существует точка В, которая плоскости не принадлежит. Через точки А и В можно провести прямую. Прямая АВ не лежит в плоскости и пересекает ее (в точке А).
Пример 2. Дана плоскость 
. Доказать, что существует другая плоскость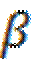 
, пересекающая 
.
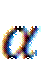Решение. Возьмем точки А и В, принадлежащие плоскости, и точку С, не принадлежащую ей (аксиома С1). Точки А, В и С не лежат на одной прямой. Через них по теореме 3 можно провести плоскость, и притом только одну. Плоскости и имеют общую точку, а значит, по аксиоме С2 плоскости и пересекаются.
Задания к практической работе
Задание 1. Через данную точку А, не принадлежащую данной плоскости, проведите прямую, параллельную.
Задание 2. Верно ли утверждение: если прямая параллельна плоскости, то она не пересекает ни одной прямой: а) лежащей в этой плоскости; б) параллельной этой плоскости? Ответ обоснуйте.
Задание 3. Известно, что прямая m параллельна плоскости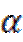 
. Параллельна ли эта прямая любой прямой, лежащей в плоскости ? Ответ обоснуйте.
Задание 4. Через данную прямую а проведите плоскость, параллельную данной прямой b. (Рассмотрите возможные случаи взаимного расположения прямых a и b)
Контрольные вопросы
1. Перечислите основные геометрические фигуры в пространстве.
2. Перечислите основные аксиомы стереометрии.
3. Докажите одну из теорем, приведенных в теоретическом материале данной практической работы.
Рекомендуемая литература: 1.2, 2.2
Практическая работа №45
