Задание 1. Каким событием (достоверным, невозможным или случайным) является событие:
1) изъятая из колоды одна карта оказалась семеркой треф;
2) при комнатной температуре и нормальном атмосферном давлении медь оказалась в жидком состоянии;
3) при температуре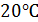 
и нормальном атмосферном давлении вода оказалась в жидком состоянии;
4) наугад названное натуральное число оказалось больше нуля;
5) вынутый наудачу цветок из букета гвоздик оказался розой;
6) в результате броска игрального кубика появилось число 5?
Задание 2. Выяснить, являются ли события А и В несовместными, если:
1) А – появление туза, В – появление дамы в результате одного изъятия одной карты из колоды карт;
2) А – появление туза, В – появление карты бубновой масти в результате одного изъятия одной карты из колоды;
3) А – выпадение числа 6, В – выпадение четного числа при одном бросании игральной кости;
4) А – выпадение числа 4, В – выпадение нечетного числа в результате одного броска игральной кости.
Задание 3. Двадцать карточек пронумерованы числами от 1 до 20. Произвольно из них выбирается одна карточка. Пусть событие А – на карточке записано число, кратное 4; событие В – на карточке записано число, кратное 6. Выяснить в чем состоят события А+В и АВ.
Задание 4. На стол бросают две игральные кости. Событие А – на первой кости выпало число 5, В – на второй кости выпало число, не меньшее пяти. Установить, в чем заключаются события А+В и АВ.
Задание 5. Пусть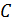 
и 
– произвольные события. Записать следующие события:
1) произошли оба данных события;
2) произошло только событие ;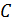
3) произошло только событие ;
4) ни одно из данных событий не произошло;
5) произошло, по крайней мере, одно из данных двух событий;
6) произошло только одно из данных событий.
Задание 6. Какова вероятность выпадения числа: 1) 2; 2) 5 в результате одного бросания игрального кубика?
Задание 7. Какова вероятность того, что при изъятии одной карты из колоды в 36 листов игрок вынет: 1) даму треф; 2) короля пик; 3) валета красной масти; 4) семерку черной масти; 5) шестерку; 6) туза; 7) или даму, или валета; 8) или восьмерку, или девятку; 9) или короля червовой масти, или даму любой масти; 10) или валета любой масти, или туза пик; 11) не короля треф; 12) не даму?
Задание 8. Какова вероятность того, что на открытом наугад листе откидного календаря на январь окажется: 1) 21-е число; 2) 10-е число; 3) 31-е число; 4) 32-е число; 5) число, содержащее в своей записи цифру 0; 6) число, содержащее цифру 4; 7) число, содержащее хотя бы одну цифру 2; 8) число, содержащее хотя бы одну цифру 1?
Задание 9. В коробке находятся 2 белых, 3 черных и 4 красных шара. Наугад вынимается один шар. Найти вероятность того, что вынутый шар: 1) белый; 2) черный; 3) красный; 4) белый или черный; 5) белый или красный; 6) черный или красный; 7) или белый, или черный, или красный; 8) синий.
Задание 10. В лотерее участвуют 100 билетов, среди которых: 1) 4 выигрышных; 2) 5 выигрышных. Наугад берут один билет. Какова вероятность того, что взятый билет выигрышный?
Задание 11. Среди 20 деталей, лежащих в ящике, 3 детали бракованные. Наугад вынимают 2 детали. Какова вероятность того, что: 1) обе детали оказались бракованными; 2) одна деталь бракованная, а другая нет; 3) обе детали не бракованные?
Задание 12. Среди 15 лампочек 4 испорчены. Наугад берут две лампочки. Какова вероятность того, что: 1) обе выбранные лампочки испорчены; 2) одна лампочка исправная, а одна – испорченная; 3) обе лампочки исправные?
Задание 13. Из полного набора домино, не глядя, извлекают две костяшки. Найти вероятность того, что: 1) обе костяшки окажутся дублями; 2) на каждой из костяшек одна половинка будет «пустой».
Задание 14. В папке находятся 15 билетов спортивной лотереи, 20 билетов художественной лотереи и 30 билетов денежно-вещевой лотереи. Найти вероятность того, что наугад вынутый из этой пачки один билет окажется билетом: 1) либо спортивной, либо денежно-вещевой лотереи; 2) либо спортивной, либо художественной лотереи; 3) либо художественной, либо денежно-вещевой лотереи. Решить задачу двумя способами.
Задание 15. Найти вероятность того, что в результате одного бросания игральной кости выпадет число, отличное от 1.
Задание 16. Найти вероятность того, что наугад вынутая из полного набора домино одна кость окажется не дублем.
Задание 17. Вероятность попадания мяча в корзину, брошенного один раз некоторым баскетболистом, равна 0,4. Найти вероятность того, что, бросив мяч в корзину, этот баскетболист промахнется.
Задание 18. Вероятность выигрыша по одному билету в некоторой лотерее равна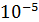 
. Какова вероятность приобретения невыигрышного билета при покупке одного билета?
Задание 19. В коробке лежат 5 белых и 7 черных шаров. Наугад вынимают 3 шара. Найти вероятность того, что среди них окажется по крайней мере один: 1) белый шар; 2) черный шар.
Задание 20. В студенческой группе 24 человека, среди которых только 6 девушек. Случайным образом из числа всех студентов выбирают троих на профсоюзную конференцию. Найти вероятность того, что среди них окажется: 1) по крайней мере одна девушка; 2) по крайней мере один юноша.
Задание 21. Выяснить, являются ли события А и В независимыми, если:
1) 
;
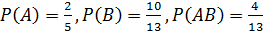2) 
;
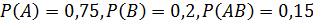3) 
;
4) 
.
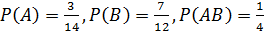Задание 22. Вероятность выигрыша на некоторой бирже в течение каждого из двух фиксированных дней равна 0,3. Найти вероятность того, что на этой бирже: 1) выигрыши произойдут в каждый из этих двух дней; 2) два этих дня не будет выигрышей; 3) выигрыши произойдут хотя бы в один из двух фиксированных дней.
Задание 23. Для сигнализации об угоне установлены два независимых датчика. Вероятность того, что при угоне сработает первый датчик, равна 0,97, что сработает второй, равна 0,95. Найти вероятность того, что при угоне: 1) сработают оба датчика; 2) оба датчика не сработают; 3) сработает хотя бы один из датчиков; 4) хотя бы один из датчиков не сработает.
Задание 24. В первой коробке находятся 7 белых и 3 черных шара, а во второй – 5 белых и 9 черных. Не глядя из каждой коробки вынимают по одному шару. Найти вероятность того, что: 1) оба вынутых шара белые; 2) оба вынутых шара черные; 3) хотя бы один шар белый; 4) хотя бы один шар черный.
Задание 25. Вероятность того, что цель будет поражена хотя бы одним из двух выстрелов, равна 0,96. Полагая, что каждый раз вероятность поражения цели при одном выстреле одна и та же, найти эту вероятность.
Задание 26. Вероятность 
того, что при измерении прибором некоторой физической величины будет допущена ошибка, превышающая заданную точность, постоянна. Вероятность того, что ошибка будет допущена этим прибором хотя бы один раз из двух измерений, равна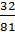 
. Найти .
Задание 27. Вероятность попадания по мишени при одном выстреле некоторым стрелком равна 0,8. Найти вероятность попадания по мишени этим стрелком: 1) в каждом из трех выстрелов; 2) хотя бы одним из трех выстрелов.
Задание 28. Заполнить последний столбец таблицы (с точностью до тысячных):
| № п/п | Испытание | Число испытаний ( )
| Наблюдаемое событие | Частота события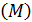 
| Относительная частота события 
|
| Брошена монета | Выпала решка | ||||
| Брошен игральный кубик | Выпало число 4 | ||||
| Спортсмен стреляет по мишени | Попадание по мишени | ||||
| Брошен игральный тетраэдр (с гранями, пронумерованными числами 1, 2, 3, 4) | Выпало число 3 |
Задание 29. Проводились серии из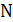 
испытаний с подбрасыванием некоторой правильной треугольной призмы, сделанной из стали. Результаты заносились в таблицу:
Число испытаний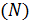 
| ||||||
Частота падения призмы на любую боковую грань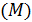 
| ||||||
Относительная частота падения призмы на боковую грань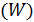 
|
Контрольные вопросы
1. Какое событие называют случайным?
2. Какое событие называют невозможным?
3. Какое событие называют достоверным?
4. Что называется объединением событий?
5. Что называется пересечением событий?
6. Какие события называются равносильными?
7. Какие события называются противоположными?
8. Дайте определение вероятности.
9. Сформулируйте теорему сложения двух вероятностей.
10. Чему равна сумма вероятностей противоположных событий?
11. Какие события называются независимыми?
12. Дайте определение относительной частоты событий.
Рекомендуемая литература: 1.1
Практическая работа №43
Тема: Основные понятия математической статистики: генеральная совокупность, выборка, среднее арифметическое, медиана
Цель: формирование навыков нахождения предела функции
Вид работы: индивидуальный
Время выполнения: 8 часов
Теоретический материал
Статистика занимается сбором, представлением (в виде таблиц, диаграмм, графиков и др.) и анализом информации о различных случайных величинах.
Случайными величинами называют такие величины, которые в ходе наблюдений или испытаний могут принимать различные значения. Можно говорить о том, что их значения зависит от случая.
Различают непрерывные и дискретные случайные величины. Дискретной случайной величиной называется такая величина, которая в результате испытания принимает отдельные изолированные значения. Например: Производится 3 выстрела по цели. Случайная величина х - это число попаданий в цель, тогда х может принимать значения: 0, 1, 2, 3.
Непрерывной случайной величиной называют случайную величину, которая может принимать все значения из некоторого промежутка. Значения могут быть конечными и бесконечными. Например: Время безаварийной работы станка; расход горючего на единицу расстояния; количество осадков, выпавших в сутки.
Случайные величины будем обозначать заглавными буквами конца латинского алфавита - X, Y, Z, а их возможные значения - соответствующими малыми буквами - х, у, z. Например, X - число шахматных партий, окончившихся ничейным результатом, из трёх сыгранных. В этом случае величина X может принять следующие значения: 
.
В статистике исследуют различные совокупности данных – числовых значений случайных величин с учетом частот, с которыми они встречаются в совокупности. При этом совокупность всех данных называют генеральной совокупностью, а любую из нее часть – выборкой. В статистических исследованиях выборку называют репрезентативной, если в ней присутствуют те и только те значения случайной величины, что и в генеральной совокупности, причем частоты имеющихся в ней данных находятся практически в тех же отношениях, что и в генеральной совокупности.
Совокупность данных иногда бывает полезно охарактеризовать (оценить) одним числом – мерой центральной тенденции числовых значений ее элементов. К таким характеристикам относятся мода, медиана и среднее.
Мода (обозначают 
) – это значение случайной величины, имеющее наибольшую частоту в рассматриваемой выборке.
Например, мода выборки 7, 6, 2, 5, 6, 1 равна 6; выборка 2, 3, 8, 2, 8, 5 имеет две моды: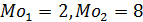 
.
Медиана (обозначают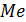 
) – это число (значение случайной величины), разделяющее упорядоченную выборку на две равные по количеству данных части. Если в упорядоченной выборке нечетное количество данных, то медиана равна серединному из них. Если в упорядоченной выборке четное количество данных, то медиана равна среднему арифметическому двух серединных чисел.
Пример 1. Найти медиану выборки значений случайной величины 1) 5, 9, 1, 4, 5, -2, 0; 2) 7, 4, 2, 3, 6, 1.
Решение. 1) Расположим элементы выборки в порядке возрастания: -2, 0, 1, 4, 5, 5, 9. Количество данных нечетно. Слева и справа от числа 4 находятся по 3 элемента, т.е. 4 – серединное число выборки, поэтому 
.
2) Упорядочим элементы выборки: 1, 2, 3, 4, 6, 7. Количество данных четно. Серединные данные выборки: 3 и 4, поэтому 
.
Среднее (или среднее арифметическое) выборки – это число, равное отношению суммы всех чисел выборки к их количеству. Среднее арифметическое обозначают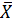 
.
Пример 2. Найти среднее выборки значений случайной величины 
, распределение которых по частотам представлено в таблице.
|
| |||||
|
.
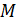
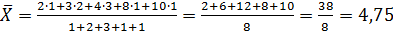Одной из наиболее распространённых характеристик выборки значений случайной величины, чье распределение по вероятностям известно, является так называемое математическое ожидание.
Пусть распределение по вероятностям 
значений некоторой случайной величины задано таблицей.
|
| 
| 
| 
| … | 
| 
|
|
| 
| 
| 
| … | 
| 
|
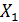
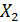
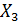
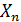
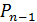
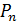
Тогда число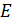 
, где
, ()
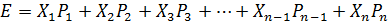Называют математическим ожиданием (или средним значением) случайной величины .
Разность наибольшего и наименьшего значений случайной величины выборки называется ее размахом и обозначается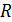 
.
Рассмотрим пример.
На место токаря претендуют двое рабочих. Для каждого из них установили испытательный срок, в течение которого они должны были изготавливать одинаковые детали. Результаты работы претендентов представлены в таблице.
Каждый из рабочих за 5 дней изготовил 250 деталей, значит, средняя производительность труда за день у обоих рабочих одинаковая:
(дет./день).
| День недели | Дневная выработка | |
Первого рабочего 
| Второго рабочего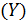 
| |
| Понедельник | ||
| Вторник | ||
| Среда | ||
| Четверг | ||
| Пятница |
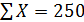
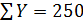
Моды у предложенных совокупностей отсутствуют, а медианы одинаковые (50 и 50). Кого же из этих рабочих предпочтительнее взять на работу? В данном случае в качестве критерия сравнения совокупностей может выступать стабильность производительности труда рабочего. Ее можно оценивать с помощью отклонений от среднего значения элементов совокупности.
Отклонением от среднего называют разность между рассматриваемым значением случайной величины и средним значением выборки.
Например, если значение величины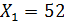 
, а значение среднего 
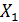, то отклонение от среднего будет равно 
.
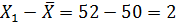Очевидно, отклонение от среднего может быть как положительным, так и отрицательным числом. Сумма отклонений всех значений выборки от среднего значения равна нулю. Поэтому характеристикой стабильности элементов совокупности может служить сумма квадратов отклонений от среднего.
| День недели | Значение случайной величины | Отклонение от среднего
| Квадраты отклонений | |||
|
| 
| 
| 
| 
| 
| |
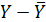
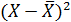
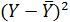
| Понедельник | -2 | |||||
| Вторник | -10 | |||||
| Среда | ||||||
| Четверг | ||||||
| Пятница | -4 | -6 | ||||
| Сумма |
Из предложенной таблицы видно, что у второго рабочего сумма квадратов отклонений от среднего больше, чем у первого рабочего:
.
На практике это означает, что второй рабочий имеет нестабильную производительность труда.
Если бы рабочие работали разное количество дней и производили в среднем за день одинаковое число деталей, то стабильность работы каждого из них можно было бы оценить по величине среднего арифметического квадратов отклонений.
Такая величина называется дисперсией и обозначается буквой .
Для случайной величины , принимающей различных значений и имеющей среднее значение 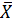, дисперсия находится по формуле
. ()
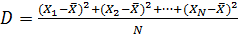Для оценки степени отклонения от среднего значения удобно иметь дело с величиной той же размерности, что и сама величина . С этой целью используют значения корня квадратного из дисперсии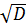 
.
Корень квадратный из дисперсии называют средним квадратичным отклонением и обозначают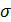 
, т.е. 
.
Дисперсию и среднее квадратичное отклонение в статистике называют также мерами рассеивания значений случайной величины около среднего значения.
Упражнения с решениями
Пример 3. Имеются результаты 20 измерений диаметра 
болта (в миллиметрах с точностью до 0,1): 10,1; 10,0; 10,2; 10,1; 9,8; 9,9; 10,0; 10,0; 10,2; 10,0; 10,0; 9,9; 10,0; 10,1; 10,0; 9,9; 10,0; 10,1; 10,1; 10,0. Представить эти данные с помощью: 1) таблиц распределения по частотам и относительным частотам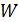 
; 2) полигона частот.
Решение. 1) Имеющиеся данные (значения случайной величины ) представим в виде таблицы распределения по частотам и относительным частотам:
|
| 9,8 | 9,9 | 10,0 | 10,1 | 10,2 |
|
| |||||
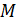
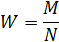
| 0,05 | 0,15 | 0,45 | 0,25 | 0,1 |
Отметим, что 
.
Пример 4. Распределение по частотам значений величины – числа забитых голов игроками футбольной команды за период соревнований показано в таблице. Найти среднее квадратичное отклонение от среднего значения числа всех забитых голов.
|
| ||||
|
|
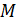
Решение. Результаты последовательных вычислений будем заносить в таблицу, при этом:
.
|
| ||||
|
| ||||
|
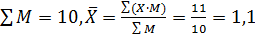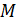
| -1,1 | -0,1 | 0,9 | 1,9 |
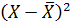
| 1,21 | 0,01 | 0,81 | 3,61 |
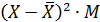
| 4,84 | 0,02 | 2,43 | 3,61 |
.
.
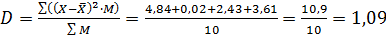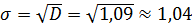