Задание 1. Составить таблицу распределения по вероятностям 
значений случайной величины 
– суммы чисел, появившихся при бросании двух игральных тетраэдров, грани которых пронумерованы натуральными числами от 1 до 4.
Задание 2. На стол бросают обыкновенный игральный кубик и игральный октаэдр, грани которого пронумерованы числами от 1 до 8. Составит таблицу распределения значений случайной величины – суммы выпавших чисел по их вероятностям .
Задание 3. Составить таблицу распределения по частотам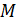 
значений случайной величины – цифр, встречающихся в выборке следующих телефонных номеров:
1) 3965184, 6542913, 7902914, 2878858.
2) 1316573, 4336582, 2983412, 3941009.
Задание 4. Построить полигон частот и полигон относительных частот значений случайной величины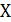 
, распределение которой представлено в таблице
|
| |||||
|
|
| ||||||
|
|
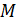
Задание 5. Составить таблицы распределения по частотам 
и относительным частотам 
, а также полигон частот значений случайной величины 
– ростов 30 девушек спортивной секции гимнастики, приведенных (с точностью до 1 см) в таблице:
Задание 6. Найти моду выборки:
1) 4, 15, 6, 7, 3, 6, 8;
2) 18, 9, 5, 3, 7, 9, 1;
3) 1, 3, 5, 1, 4, 3, 2;
4) 6, 8, 5, 4, 8, 3, 6.
Задание 7. Найти медиану выборки:
1) 17, 12, 34, 18, 6;
2) 24, 15, 13, 20, 21;
3) 4, 1, 8, 9, 13, 10;
4) 15, 6, 12, 8, 9, 14.
Задание 8. Найти среднее значение выборки:
1) 24, -5, 13, -8;
2) 7, 16, -9, -2, 10;
3) 0,3, 0,8, 0,2, 0,5, 0,8, 0,2;
4) 1,3, 1,4, 1,3, 0,9, 0,9, 1,4.
Задание 9. Найти моду, медиану и среднее выборки:
1) 3, -2, 1, 0, 2, -1;
2) 7, 4, -1, 3, -3, 0.
Задание 10. Найти математическое ожидание значений случайной величины 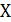, распределение которых по вероятностям представлено в таблице:
|
| -3 | -1 | ||
|
| 
| 
| 
|
|
|
| -1 | ||||
|
| 
| 
| 
| 
|
|
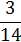
Задание 11. Найти размах выборки:
1) 15, -7, 13, -6, 8, 2, 1, -8, -2;
2) 21, 12, -1, 7, -3, 20, 14, 0, 1.
Задание 12. Найти дисперсию выборки:
1) 10 см, 12 см, 7 см, 11 см;
2) 16 г, 14 г, 13 г, 17 г;
3) 11 с, 14 с, 11 с, 12 с, 12 с;
4) 5 м, 13 м, 8 м, 12 м, 12 м.
Задание 13. Найти среднее квадратичное отклонение от среднего значения элементов выборки:
1) 3 кг, 5 кг, 5кг, 8 кг, 4 кг;
2) 12 м, 10 м, 7 м, 12 м, 9 м.
Задание 14. Сравнить дисперсии двух выборок, имеющих одинаковые средние значения:
1) 6, 10, 7, 8, 9 и 8, 9, 5, 10;
2) 5, 12, 7, 8, 18 и 17, 6, 11, 7, 9, 10.
Задание 15. Найти среднее квадратичное отклонение величины 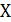, заданной частотным распределением:
|
| ||||
|
|
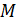
Задание 16. Сравнить дисперсии выборок, имеющих разные средние значения:
1) 4, 6, 8, 9, 8 и 6, 8, 10, 12, 9;
2) 6, 3, 4, 8, 9 и 2, 6, 3, 7, 5, 7.
Контрольные вопросы
1. Дайте определение случайной величины.
2. Какие виды случайных величин вы знаете? Приведите примеры.
3. Что называется генеральной совокупностью?
4. Что называется выборкой?
5. Дайте определение моды, медианы и среднего арифметического.
6. Как вычислить математическое ожидание случайной величины?
7. Дайте определение отклонения от среднего.
8. Что называется дисперсией?
9. Как вычислить дисперсию?
10. Дайте определение среднего квадратичного отклонения.
Рекомендуемая литература: 1.1, 1.3, 2.1
Практическая работа №44
Тема: Прямые и плоскости в пространстве
Цель: формирование навыков решения задач на доказательство существования прямых и плоскостей, используя основные аксиомы стереометрии
Вид работы: индивидуальный
Время выполнения: 6 часов
Теоретический материал
Основными геометрическими фигурами в пространстве являются точка, прямая и плоскость.
Плоскости обозначаются строчными греческими буквами:
