Дабы избежать неопределенности в оценивании отношения оддов OR, возникающей при наличии нулевых численностей в анализируемой таблице перекрестной классификации 2´2, точечную статистическую оценку OR и ДИ для него лучше производить с поправками по формулам:
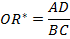
где
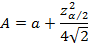
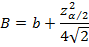
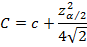
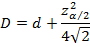
Для нахождения 100(1 – α)%-го ДИ для оцениваемого значения OR находят cтандартную ошибку для его логарифма lnOR по формуле:
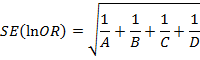
Тогда статистическими оценками границ 100(1 – α)%-го ДИ для оцениваемого значения OR будут:
Статистическая оценка нижней границы:
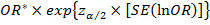
Статистическая оценка верхней границы:
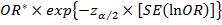
Источник:
Bolboacă S., Cadariu A.A. Binomial distribution sample confidence intervals estimation.
5. Odds ratio // Leonardo Journal of Sciences, 2004. – No. 4. – P. 26-43.
URL: http://ljs.academicdirect.org/A04/26_43.htm
Элементы планирования эксперимента в клинико-лабораторных диагностических исследованиях
Оценка объемов выборок для надежной оценки PPV и NPV в клинико-лабораторных диагностических при формировании выборок по схеме «случаи-контроли».
Оптимальное соотношение объемов выборок субъектов с болезнью и без нее для оценки PPV:
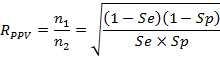
Для любого приемлемого диагностического теста Se + Sp > 1. Это означает, что это отношение всегда меньше 1. Например, если мы ожидаем, что и чувствительность и специфичность должны быть не меньше 0,8, то исследование должно включать в 4 раза больше прациентов без болезни, чем с болезнью. Если Se и Sp обе равны 0,9, то оптимальным будет соотношение 9:1. Если же объемы выборок будут равными, то асимтотические дисперсии оценок PPV будут, соответственно, на 36% и 64% больше, чем при указаных оптимальных соотношениях.
Ситуация с NPV симметрична. В этом случае оптимальное соотношение пациентов с болезнь и без нее задается выражением:
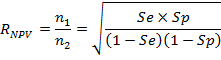
Таким образом, RNPV = 1 − RPPV и оптимальное соотношение для NPV требует больше субъектов с болезнью.
Интересное свойство заключается в том, что оптимально соотношение объемов выборок не зависит от распространенности болезни.
Для вычисления соотношения числа субъектов с болезнью и без нее до начала исследования необходимы предварительные оценки чувстивтельности и специфичности.
При некоторых исследованиях бывает так, что стоимость тестирования больных субъектов может превышать таковую для субъектов без болезни. Подобные различия в стоимости можно довольно легко учесть при планировании объемов выборок. Для этого в указанные формулы вводят величину с, которая есть соотношение стоимостей тестирования субъектов с болезнью и без нее:
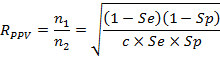
для PPV и
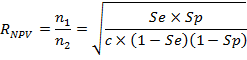
для NPV.
Минимально необходимые объемы выборок находят по формулам:

- для PPV и:
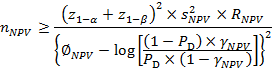
для NPV.
Здесь:
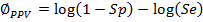
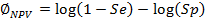
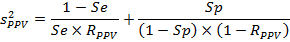
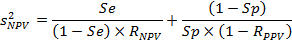
α – предпочитаемый исследователем уровень значимости, (1 – β) – предпочитаемая исследователем статистическая мощность, (1 – γ PPV) и (1 – γ NPV) минимальные значения PPV и NPV, которыми по мнению исследователя должен обладать проверяемый клинико-лабораторный диагностический тест (ПКЛДТ).
Источник:
Steinberg D.M., Fine J., Chappell R. Sample size for positive and negative predictive value in diagnostic research using case–control designs // Biostatistics, 2009. - Vol. 10. - N 1. – P. 94–105.
[1] По: Newman T.B., Kohn M.A. Evidence-Based Diagnosis. – Cambridge et al.: Cambridge University Press, 2009. – 295 p.
[2] По: Peacock J.L., Peacock P.J. Oxford Handbook of Medical Statistics. – New York: Oxford University Press, 2011. – 517 p.
[3] По: Королев В.Ю. Теория вероятностей и математическая статистика: учеб. – М.: ТК Велби, Изд-во Проспект, 2008. – 160 с.
[4] По: Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное издание. – М.: Финансы и статистика, 1983. – 471 с.
[5] По: Hopkins W.G. A Scale of Magnitude for Effect Statistics // A New View of Statistics (http://www.sportsci.org/resource/stats/)






