Если 100(1 - a)%-й доверительный интервал (ДИ) для отношения шансов накрывает практически бесполезное (неинформативное) значение OR = 1, то у нас нет оснований считать, что оцениваемое значение OR статистически значимо отличается от 1.
Если 100(1 - a)%-й ДИ для OR не накрывает значение OR = 1, то у нас появляется основание сомневаться в том, что оцениваемое значение OR равно 1.
Это является следствием того факта, что при многократных повторениях диагностического исследования границы ДИ для OR неизбежно будут варьировать, однако, доля тех из них, которые накроют значение OR = 1, не превысит выбранного нами уровня значимости a.
Статистическая значимость OR
Когда ДИ для OR не накрывает значение OR = 1, то в таких случаях говорят, что оцениваемое (неизвестное) значение OR статистически значимо отличается от 1 на уровне значимости a.
Например, если выбрана доверительная вероятность (1 - a) = 0,99, и полученный 99%-й ДИ OR не накрывает значение 1, тогда оцениваемое значение OR статистически значимо отличается от 1 на уровне значимости 0,01.
Словесная интерпретация градаций для OR [5]
| OR | Интерпретация степени согласованности |
| 1 – 1,5 | Практически ничтожная |
| 1,5 – 3,5 | От ничтожной до слабой |
| 3,5 – 9,0 | От слабой до умеренной |
| 9,0 – 32 | От умеренной до сильной |
| 32 – 360 | От сильной до очень сильной |
| >360 | Практически идеальная |
Коэффициенты каппа Коуэна
В общем виде их точечная статистическая оценка задается выражением:
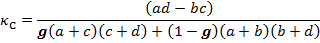
Имеют смысл три значения для «веса» g: 0; 0,5 и 1
При g = 0,5 этот коэффициент принимает «каноническую» форму:
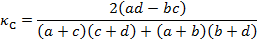
При g = 0 получается взвешенный коэффициент, который принимает во внимание исключительно влияние ложных негативов:
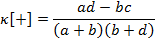
При g = 1 получается взвешенный коэффициент, который принимает во внимание исключительно влияние ложных позитивов:
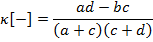
Низкое значение κ [-] указывает на высокую долю ложных негативов, в то время как тест, для которого κ [-] приближается к 1, будет давать мало ложных негативов и, следовательно, будет иметь высокую точность при исключении болезни.
И наоборот, низкое значение κ [+] указывает на высокую долю ложных позитивов, в то время как тест, для которого κ [+] приближается к 1, будет давать мало ложных позитивов и, следовательно, будет иметь высокую точность при выявлении болезни.
Статистическая интерпретация ДИ для κC
Если 100(1 - a)%-й доверительный интервал (ДИ) для коэффициента каппа Коуэна κ C накрывает практически бесполезное (неинформативное) значение κ C = 0, то у нас нет оснований считать, что оцениваемое значение κ C статистически значимо отличается от 0.
Если 100(1 - a)%-й ДИ для κ C не накрывает значение κ C = 0, то у нас появляется основание сомневаться в том, что оцениваемое значение κ C равно 0.
Это является следствием того факта, что при многократных повторениях диагностического исследования границы ДИ для κ C неизбежно будут варьировать, однако, доля тех из них, которые накроют значение κ C = 0, не превысит выбранного нами уровня значимости a.
Статистическая значимость κC
Когда ДИ для κ C не накрывает значение κ C = 0, то в таких случаях говорят, что оцениваемое (неизвестное) значение κ C статистически значимо отличается от 0 на уровне значимости a.
Например, если выбрана доверительная вероятность (1 - a) = 0,99, и полученный 99%-й ДИ κ C не накрывает значение 0, тогда оцениваемое значение κ C статистически значимо отличается от 0 на уровне значимости 0,01.






