Построение доверительных интервалов (ДИ) для индекса Юдена есть частный случай общей задачи построения ДИ для разности двух независимых долей.
Возможны два подхода: частотнический и бейзовский.
Частотнический подход
Поэтому введем общие обозначения: P 1 и P 2 – две независимые доли (вероятности); оценить надо 100(1-α)%-х ДИ для их разности: 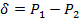
Задача не имеет точного решения, поэтому для ее решения предложено множество различных приближенных процедур.
Один из приемлемых способов такой:
Точечными статистическими оценками вероятностей P 1 и P 2 являются наблюдаемые частоты:

и
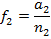
А точечной статистической оценкой разности этих вероятностей является:

Для каждой из оцениваемых вероятностей P 1 и P 2 находят статистические оценки границ приближенных 100(1-α)%-х ДИ для каждой доли по отдельности:
Для первой доли:
Статистическая оценка нижней границы 100(1-α)%-го ДИ:
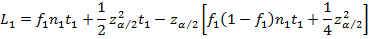
Статистическая оценка верхней границы 100(1-α)%-го ДИ:

Здесь

Для второй доли:
Статистическая оценка нижней границы 100(1-α)%-го ДИ:
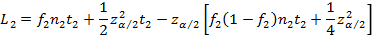
Статистическая оценка верхней границы 100(1-α)%-го ДИ:

Здесь
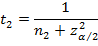
Тогда статистическими оценками нижней границы 100(1-α)%-го ДИ для оцениваемой разности двух независимых вероятностей может служить:
Статистическая оценка нижней границы 100(1-α)%-го ДИ:

Статистическая оценка верхней границы 100(1-α)%-го ДИ:

Источники:
Agresti A., Caffo B. Simple and effective confidence intervals for proportions and differences of proportions result from adding two successes and two failures // The American Statistician, 2002. - Vol. 54. - No. 4. P. 280-288.
Newcombe R.G. Interval estimation for the difference between independent proportions: comparison of eleven methods // Statist. Med., 1998. – Vol. 17. – N 8. – P. 873—890.
Бейзовский подход
Границы бейзовского 100(1-α)%-го ДИ для разности двух независимых долей можно приближенно вычислить по формулам:
Для нижней границы:
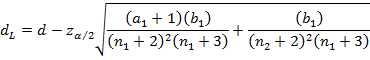
Для верхней границы:

Источник:
Agresti A., Caffo B. Simple and effective confidence intervals for proportions and differences of proportions result from adding two successes and two failures // The American Statistician, 2002. - Vol. 54. - No. 4. P. 280-288.
Доверительный интервал для коэффициента каппа Коуэна
Для построения 100(1 – α)%-го ДИ для коэффициента каппа Коуэна вычисляют стандартную ошибку его точечной оценки по приближенной формуле (по Garner, 1991):

Тогда нижней границей 100(1 – α)%-го ДИ будет: 
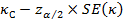
А верхней границей 100(1 – α)%-го ДИ будет:
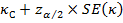
Источник:
Blackman N.J.-M., Koval J.J. Interval estimation for Cohen' s kappa as a measure of agreement // Statist. Med., 2000. – Vol. 19. – N 5. - P. 723 – 741.






