План темы
I. Методика изучения особых случаев умножения и деления чисел.
II. Теоретическая основа внетабличного умножения чисел и методика ее изучения.
III. Методика ознакомления учащихся с вычислительными приемами внетабличного приемами внетабличного умножения чисел.
IV. Теоретическая основа внетабличного деления чисел и методика ее изучения.
V. Методика ознакомления учащихся с вычислительными приемами внетабличного деления чисел.
Основное содержания
- Особые случаи умножения и деления – это случаи умножения и деления с 0 и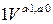 
, так как они не могут быть объяснены с общих позиций конкретного смысла действий (нет суммы из одного или нуля слагаемых). Поэтому случаи вида: 
, 
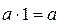вводятся как правила.
- Аналогичным образом вводится правило: «На нуль делить нельзя!».
- Приему умножения числа 1 на любое число и умножения числа 0 на любое число вводятся на основе конкретного смысла действия умножения как суммирование одинаковых слагаемых.
В записях 1 ∙ 5; 0 ∙ 3 первый множитель показывает, какое число суммируем, а второй множитель – сколько раз берем слагаемым первый множитель:
1 ∙ 5 = 1 + 1 + 1 + 1 + 1 = 5 => 1 ∙ a = a
0 ∙ 3 = 0 + 0 + 0 + 0 + 0 => 0 ∙ в = 0
- Для деления чисел на число и само на себя теоретической основой является правило взаимосвязи компонентов умножения и деления:
a ∙ b = с => с: в = а;
поэтому: 1 ∙ a = a => a: 1 = a; a: a = 1, если а ≠ 0;
0 ∙ в = 0 => 0: в = 0, в ≠ 0.
- К внетабличным случаям умножения и деления чисел в пределах 100 относятся случаи:
а) умножение двузначного числа на однозначное и однозначного числа на двузначное;
б) деление двухзначного числа на однозначное, когда в частном получается двузначное число;
в) деление двузначного числа на двузначное.
- Теоретическая основа внетабличного умножения числа включает:
а) правило умножения суммы на число;
б) переместительное свойство умножения;
в) сочетательное свойство умножения.
- В основе разъяснения правила умножения суммы на число лежит опора на знание конкретного смысла действия умножения:
а) схематическая иллюстрация:
ООО ∆
ООО ∆;
б) Математические записи для подсчета геометрических фигур:
(3 + 1) ∙ 2 = 4 ∙ 2 = 8
3 ∙ 2 + 1 ∙ 2 = 6 + 2 = 8;
в) сравнение записей и формулировка правила:
«Чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные произведения сложить».
- Переместительное свойство умножения изучалось перед составлением таблицы умножения однозначных чисел на постоянный второй множитель.
- Для разъяснения переместительного свойства применялся метод подсчета фигур по столбцам и по строкам:
ООО 2 ∙ 3 = 6
ООО 3 ∙ 2 = 6
Сравнение записей позволяет сформулировать правило «От перестановки множителей произведение не меняется».
Применение конкретного смысла действия умножения для вычислений в случаях вида: 2 ∙ 9 и 9 ∙ 2 приводит учащихся к выводу о том, что удобнее большее число умножать на меньшее.
- В основе разъяснения сочетательного свойства умножения лежит конкретный смысл действия умножения и правило перестановки множителей:
а) схематическая иллюстрация с помощью числовых фигур;
б) математические задания для подсчета числовых фигур:
(4 ∙ 3) ∙ 2 = 24
4 ∙ (3 ∙ 2) = 24
(4 ∙ 2) ∙ 3 = 24
в) рассматривая три способа вычисления результатов с опорой на анализ рисунка, ученики формулируют правило: «Перемножать числа можно в любом порядке. Результат умножения не зависит от порядка выполнения умножения».
- Вычислительные приемы внетабличного умножения чисел:
1) умножение чисел, оканчивающихся нулем:
а) 20 ∙ 3 = 2 дес. ∙ 3 = 6 дес. = 60;
б) 2 ∙ 30 = 30 ∙ 2 = 3 дес. ∙ 2 = 6 дес. = 60.
Вычислительный прием сводится к табличному умножению чисел, одно из которых – число десятков в заданных множителях.
2) прием умножения двузначного числа на однозначное:
3
а) 
23 ∙ 4 = 20 ∙ 4 + 3 ∙ 4 = 80 + 12 = 92
 |
При умножении двузначного числа на однозначное актуализируются следующие знания, являющиеся теоретической основой операции вычислительного приема: разрядный состав числа; правило умножения суммы на число; умножение целых десятков; таблица умножения; сложение двузначных чисел;
б) 4 ∙ 23 = 23 ∙ 4 – прием перестановки множителей, основанный на знании переместительного свойства умножения.
- Теоретическая основа внетабличного деления чисел включает:
а) правило деления суммы на число;
б) связь деления и умножения.
- Методика разъяснения правила деления суммы на число:
а) схематические иллюстрации и соответствующие записи:
?????
б) сравнение записей и формулировка правила: «Чтобы разделить сумму на число, можно каждое слагаемое разделить на это число и полученные частные сложить».
- Методика изучения связи деления и умножения может включать следующую последовательность учебных действий:
1) предметная или схематическая иллюстрация и соответствующая запись действия умножения: ∆ ∆ ∆ => 3 ∙ 2 = 6 (1)
∆ ∆ ∆
2) разбиение множества из 6 предметов в группы на 3 предмета:
∆∆∆ ∆∆∆ и соответствующая запись: 6: 3 = 2 (2)
3) разбиение множества из 6 предметов поровну в 2 группы
∆∆∆ ∆∆∆ и соответствующая запись: 6: 2 = 3 (3)
4) повторение названий компонентов в 1=й записи: первый множитель – 3; 2-й множитель – 2; произведение – 6;
5) какое действие мы с ними выполнили и что получили во 2 и 3 действии? Ученики отвечают: «Произведение разделили на 1-й множитель, получили 2-й множитель. Произведение разделили на 2-й множитель, получили 1-й множитель».
6) Формулируется правило: «Если произведение разделить на один из множителей. то получится второй множитель». Значит, по примеру на умножение можно составить 2 примера деления:
а ∙ в => с: а = в;
с: в = а.
Поэтому чтобы разделить одно число на другое, надо найти такое число, умножив которое на делитель, получим делимое: с: а = в => в ∙ а = с.
- Вычислительные приемы внетабличного деления чисел:
1) деление чисел, оканчивающихся нулем:
а) 80: 4 = 8 дес.: 4 = 2 дес. = 20 – прием представления круглых двузначных чисел, в виде разрядных единиц и табличное деление;
б) 80: 20 = ….
20 ∙ 4 = 80
80: 20 = 4 – прием подбора частного, основанный на связи деления и умножения;
2) прием деления двузначного числа на однозначное:
а) 36: 3 = (30 + 6): 3 = 30: 3 + 6: 3 = 10 + 2 = 12;
б) 36: 2 = (20 + 6): 2 = 20: 2 + 16: 2 = 10 + 8 = 18 – прием основанный на свойстве деления суммы разрядных слагаемых или удобных слагаемы на число;
3) прием делении двузначного числа на двузначное:
56: 14 = ….
14 ∙ 4 = 56
56: 14 = 4 – прием подбора частного, основанный на связи деления и умножения.
