1.Изменение коэффициента усиления САР.
Для главной цели характерным является последовательное соединение звеньев 
причем коэффициент усиления САР 
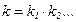находится в числителе передаточной функции.
Увеличение k увеличивает j(v) и f(v) и расширяет АФХ, приближая ее к критической точке (-1, j0).
При значительном увеличении коэффициента усиления САР может стать неустойчивой.
Рисунок 6.12 Влияние на устойчивость САУ коэффициента усиления
Влияние на устойчивость последовательного включения апериодического звена.
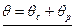
Для апериодического звена фаза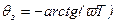 
, т.е. при построении результирующей АФХ каждый из векторов надо поворачивать на угол qз и одновременно увеличивать модуль 
. При этом все точки АФХ приблизятся к критической
(-1,j0) и устойчивость САР уменьшиться.
Вывод: чем больше постоянная времени звена T, тем больше будет Qз, больше разворот АФХ к критической точке, больше склонность САР к неустойчивости.
То же будет и при включении последовательно с системой нескольких апериодических звеньев.
Последовательное включение в главную цепь устойчивого звена второго порядка подобно поведению САР при включении двух апериодических звеньев, т.к.
.
В статической САР отсутствуют интегрирующие звенья. Тогда при v=0 точка АФЧХ лежит на положительном луче вещественной оси, т.к. 
, т.е. при v=0, W(jv)=k.
Рисунок 6.13 Влияние коэффициента усиления на точку v=0
При включении последовательно со статической САР интегрирующего звена 
и 
каждый из векторов системы, определяемый скобками, повернется на угол 
.
и при v=0 W(jv)=-j¥, т.е. при малых положительных значениях v АФЧХ располагается в III квадранте и при w®0 уходит в -j¥. Такая система с одним интегрирующим звеном называется САР с астатизмом первого порядка.
Вывод: последовательное включение в систему интегрирующего звена резко ухудшает устойчивость САР.
Рисунок 6.14 Различия между АФЧХ статической и астатической систем
Включение последовательно со статической САР двухкратноинтегрирующих звеньев.
При включение последовательно со статической САР двухкратноинтегрирующих звеньев получается САР с астатизмом второго порядка:
при малых значениях v АФЧХ располагается уже во втором квадранте и при v=0 
.
Рисунок 6.15 АФЧХ двукратно интегрирующей системы
Вывод: при включении последовательно со статической САР двухкратноинтегрирующих звеньев АФХ полученной САР всегда охватывает точку (-1,j0) и САР будет неустойчивой при любых параметрах системы. Это явление носит название структурной неустойчивости САР.
Запас устойчивости САУ
Запас устойчивости по фазе и запас устойчивости по модулю.
Назовем разность между углом -p и фазой q(v) вектора АФЧХ избытком фазы 
. Тогда запас устойчивости по фазе g определяется наименьшей величиной избытка фазы при модуле A(v)=1.
Запас устойчивости по модулю h определяется отрезком вещественной оси между критической точкой и АФЧХ. Частоту vср соответствующую точке АФЧХ с A=1 называют частотой среза разомкнутой САР. vср определяет ту частоту, с которой начинают меняться усилительные свойства звена или системы, т.е.
, т.е. 
,
при v<vср 
, т.е. 
,
при v>vср 
, т.е. 
.
Рисунок 6.16 К определению запаса устойчивости по фазе и по модулю
В этом случае система имеет коэффициент усиления меньше единицы, т.е. колебания затухают быстрее, система пассивна и при дальнейшем увеличении v амплитуда выходного сигнала продолжает уменьшаться.
Рисунок 6.17 Частотная характеристика системы, отличающейся коэффициентом усиления
Рисунок 6.18 К определению запаса устойчивости по амплитуде
Запас устойчивости может быть выражен в процентах
Если запас устойчивости по модулю и фазе задан, то можно построить запретную зону на комплексной плоскости АФХ в которую не должна заходить АФХ системы.
Считают достаточным g=30°; желательно 45°.
Если АФХ сложной формы, то наше определение запаса устойчивости может дать неверное представление о действительном запасе устойчивости.
В этом случае запас устойчивости по модулю определяется не отрезком вещественной оси, а наименьшим значением разности между модулем АФХ и единицей при избытке фазы в пределах ±g.
Рисунок 6.19 Определение запаса устойчивости по амплитуде при сложной форме АФХ
Рисунок 6.20 Определение запаса устойчивости по фазе при сложной форме АФХ
