В качестве оценок качества переходного процесса принимаются определенные интегралы отклонения выходной величины Y от нового установившегося состояния.
Оценки выбираются так, чтобы они с одной стороны характеризовали переходный процесс, а с другой выражались бы через параметры системы, такими оценками являются интегралы.
; (7.3)
Выражение (7.3) представляет собой линейную интегральную оценку.
; (7.4)
, (7.5)
Критерий (7.5) характеризует квадратичную интегральную оценку, где 
.
Интеграл (7.3) выражает площадь между кривыми переходного процесса и установившимся значением Y(¥) (рисунок 7.6).
Чем меньше эта площадь I1, тем быстрее производится регулирование, тем лучше, таким образом, имеется минимум интеграл (7.3) и соответствующие этому минимуму параметры системы.
Выражение (7.3) примем для монотонной Y(t) без перерегулирования и смены знака. Если Y(t) - колебательна, то для такой Y(t) площади будут вычитаться, и для неустойчивого режима автоколебаний будим иметь 0 I1 (площади) (рисунок 7.7).
Для оценки колебательного процесса надо использовать квадратичный критерий (7.4).
Этот критерий основан на приближении кривой Y(t) к форме скачка, которую имеет входное воздействие, если пишется минимум I2.
Геометрически это будет выглядеть так: кривая переходного процесса MLN будет тем ближе к идеальной кривой MON, чем меньше будет интеграл I2. Но опыт показывает, что, создавая такое быстродействие (при минимуме I2), Y(t) будет колебательным (тоже и с I1) (рисунок 7.8).
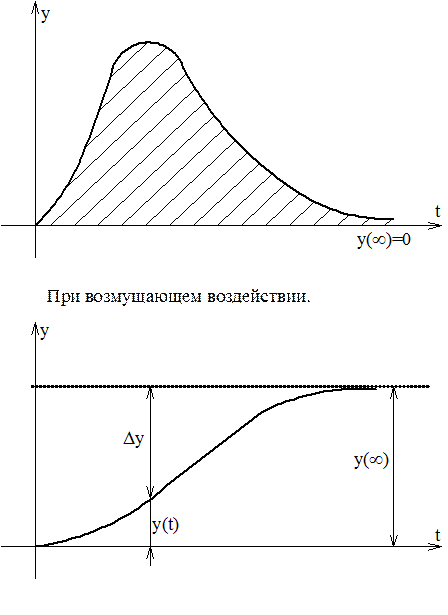
Рисунок 7.6 Линейная интегральная оценка
Рисунок 7.7 Кривая y(t) при неустойчивом режиме автоколебаний.
Рисунок 7.8 К оценке колебательного процесса.
Когда этот критерий неприменим, то переходят к критерию (7.5). Интеграл (7.5) состоит из 2-х частей. Первый интеграл является I2, а второй интеграл от 
, т.е. от квадрата скорости изменения Dy во времени.
Преобразуем (7.5):
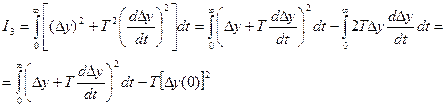
т.е. I3 будет минимальным, если 
, откуда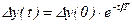 
, но так как 
, то 
.
При наименьшем интеграле (7.5) переходный процесс протекает по экспоненте с определенной постоянной времени. Если в случае наименьшей квадратичной ошибки (7.5) мы стремились приблизить переходный процесс к скачкообразной функции, то в случае (7.5) переходной процесс приближаем к экспоненте, смягчая условие оптимальности и задавая некоторое замедление (рисунок 7.9).
Рисунок 7.9 Кривая переходного процесса при квадратичной интегральной оценке
В заключении укажем основные области применения рассмотренных критериев.
Частотные и интегральные критерии используются при исследовании качества переходных процессов, вызванных основными (главными) воздействиями. Эти критерии позволяют учесть конкретную форму воздействия и начальные условия.
Интегральные критерии применяются в этом же случае для определения оптимального значения какого-либо варьируемого параметра; численной оценки показателя качества они не дают.
Корневые критерии используются главным образом для оценки в среднем качества переходных процессов при всевозможных воздействиях и начальных условиях.
Для систем выше пятого порядка применяются, в основном, частотные критерии.
