Этот критерий позволяет исследовать устойчивость замкнутой системы по частотным характеристикам разомкнутой системы, которые можно получить как аналитически, так и экспериментально. Эти обстоятельства выгодно отличают рассматриваемый критерий от ранее изложенных. Заметим, что критерий Найквиста применим только для систем с единичной обратной связью.
Пусть передаточная функция разомкнутой системы регулирования
, (6.30)
где Dp(p) - характеристический полином разомкнутой системы.
Передаточная функция системы, замкнутой единичной обратной связью, будет иметь вид:
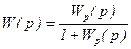, (6.31)
где
, (6.32)
Числитель выражения (6.32) представляет характеристический полином замкнутой системы, знаменатель - характеристический полином разомкнутой системы. При этом соблюдается условие m<n, где m - степень характеристического полинома K(p), а n - степень характеристического полинома D(p). Выполнение этого условия обеспечивает удовлетворение равенства
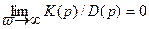. (6.33)
Рассмотрим три случая состояния разомкнутой системы: устойчива, неустойчива и находится на границе устойчивости, причем в последнем случае характеристическое уравнение разомкнутой системы Dp(p)=0 имеет нулевой порядок астатизма n, т.е. Dp(p)=pn×D1(p).
1.Система в разомкнутом состоянии устойчива.
Согласно критерию Михайлова, изменение аргумента характеристического полинома устойчивой разомкнутой системы, при изменении v от 0 до ¥
.
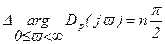Если потребовать, чтобы система и в замкнутом состоянии должна оставаться устойчивой, то должно быть удовлетворено равенство:
.
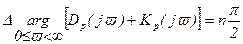Тогда из (6.32) следует
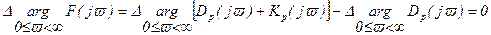(6.34)
Таким образом, система автоматического регулирования устойчива, если изменение аргумента вектора F(jv) при изменении v от 0 до ¥ равно 0. Это означает, что годограф F(jv) (рисунок 6.8, а, кривая 1) для устойчивой системы не охватит начало координат и, наоборот, для неустойчивой системы охватит точку с координатами (0, j0) (рисунок 6.8, а, кривая 2). Поскольку F(jv) отличается от Wp(jv) на +1, то условие устойчивости можно получить непосредственно для характеристики Wp(jv) (рисунок 6.8, б).
Приведем формулировку критерия Найквиста для этого случая.
Для устойчивой замкнутой системы автоматического регулирования необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи (частотной передаточной функции) разомкнутой системы Wp(jv) при изменении v от 0 до ¥ не охватывая точку (-1, j0).
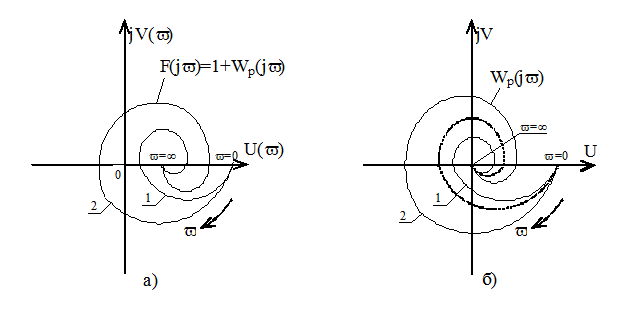
Рисунок 6.8 Амплитудно-фазовая характеристика, соответствующая устойчивой и неустойчивой системе
Применим критерий Найквиста для определения предельного коэффициента усиления разомкнутой системы, представленной на рисунке 6.3. Для этого структурную схему преобразуем к виду показанному на рисунке 6.9.
Чтобы определить значение Kкр, необходимо найти значение Kр, при котором годограф проходит через точку (-1; j0), т.е. решить уравнение
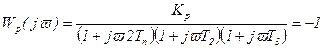, (6.35)
или
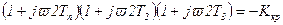(6.36)
Представив (6.36) в виде действительной и мнимой части, получим:
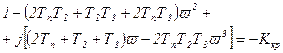(6.37)
Рисунок 6.9 Структурная схема
Очевидно, что в выражении (6.37) мнимая часть должна быть равна нулю. Это возможно при соблюдении условия
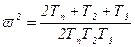, (6.38)
Подставляя (6.38) в (6.37) получим
, (6.39)
что совпадает с (6.16).
2.Система в разомкнутом состоянии неустойчива.
При рассмотрении многоконтурных или одноконтурных САУ они могут оказаться неустойчивыми в разомкнутом состоянии, т.е. характеристическое уравнение разомкнутой системы может иметь правые корни.
Пусть система в разомкнутом состоянии неустойчива, при этом характеристическое уравнение разомкнутой системы имеет a корней в правой полуплоскости. Тогда результирующий угол поворота вектора Dp(jv) будет складываться из следующих составляющих:
1) n-a «левых» корней при изменении v от 0 до ¥ обеспечат угол поворота 
;
2) a «правых» корней обеспечат отрицательный угол поворота 
;
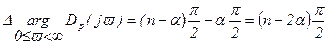, (6.40)
Если потребовать, чтобы в замкнутом состоянии система была устойчива, то должно выполняться равенство
. (6.41)
При этом с учетом (6.33)
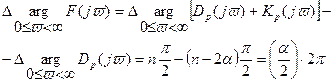, (6.42)
Отсюда следует формулировка критерия Найквиста: для устойчивости замкнутой системы автоматического регулирования, неустойчивой в разомкнутом состоянии, необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы Wp(jv) при изменении v от 0 до ¥ охватывая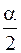 
раз в положительном направлении точку (-1; j0), где a - число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости. Очевидно, что формулировка критерия Найквиста для первого случая является частным случаем (a=0) только что приведенной формулировки.
3.Система в разомкнутом состоянии находится на границе устойчивости.
Передаточная функция в разомкнутом состоянии
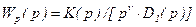, (6.43)
где n - число нулевых корней характеристического уравнения системы в разомкнутом состоянии. Этот случай соответствует астатической САУ, причем n - порядок астатизма.
В этом случае принцип аргумента, положенный в основу критерия Найквиста не рассматривает варианты, когда корни находятся на мнимой оси. Рассмотрим возможность применения критерия Найквиста для этого случая.
Произведем искусственный сдвиг нулевых корней (pi=±a) с последующим предельным переходом (a®0). Тогда при n=1 передаточную функцию (6.43) можно записать в виде:
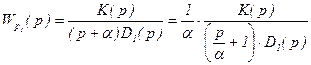, (6.44)
При этом интегрирующее звено превратилось в инерционное с постоянной времени и коэффициентом усиления равным 1/a. Это соответствует смещению влево нулевого корня (рисунок 6.10, а). Частотные годографы Wp(jv) и Wp1(jv) (рисунок 6.10, б) близки друг к другу. При a®0 они совпадают на всех частотах, кроме v=0. Годограф Wp1(jv) отличается от Wp(jv) наличием дуги бесконечного радиуса, проходящей через IV квадрант и приводящей годограф при v®0 к действительной положительной полуоси (рисунок 6.10, в). Эту часть годографа называют дополнением в бесконечности.
Аналогично строятся измененные частотные годографы при n=2,3. В этом случае дополнение проходит через число квадрантов, равное порядку астатизма, т.е. дуга бесконечно большого радиуса описывает угол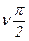 
в отрицательном направлении вокруг начала координат (рисунок 6.10, г).
Для частотных годографов разомкнутых систем, дополненных в бесконечности, можно пользоваться первой формулировкой критерия Найквиста.
Для устойчивой замкнутой системы автоматического регулирования, которая в разомкнутом состоянии находится на границе устойчивости, имея нулевые корни характеристического уравнения, необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы Wp(jv), дополненный в бесконечности, при изменении v от 0 до ¥ не охватывал точку (-1; j0).
Наиболее общая формулировка критерия Найквиста основана на подсчете числа переходов частотного годографа через отрицательную действительную полуось от -1 до -¥. При этом переход считается положительным, если при возрастании v годограф переходит из верхней полуплоскости в нижнюю и отрицательным, если годограф переходит из нижней полуплоскости в верхнюю.
Рисунок 6.10 Частотные годографы
Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы разность между числами положительных и отрицательных переходов частотного годографа комплексного коэффициента передачи разомкнутой системы Wp(jv) через отрицательную действительную полуось от -1 до -¥ была равна a/2, где a число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.
Для систем находящихся в разомкнутом состоянии на границе устойчивости с нулевыми корнями характеристического уравнения, число a считается равным нулю, а годограф Wp(jv) берется с дополнением в бесконечности.
Рисунок 6.11 Частотные годографы
