Это алгебраический критерий, по которому условия устойчивости сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы. В разной форме этот критерий был предложен английским математиком Е. Раусом (1872 г.) и затем швейцарским математиком А. Гурвицем (1895 г.). Приведем без доказательства этот критерий в форме Гурвица.
Возьмем характеристический полином, определяющий левую часть дифференциального уравнения системы:
, (6.7)
где полагаем a0>0, что всегда можно обеспечить умножением, при необходимости, полинома на -1. Из коэффициентов этого уравнения построим квадратную матрицу (таблицу) Рауса-Гурвица. Эта матрица называется определителем Гурвица. Он имеет n строк и n столбцов.
, (6.8)
Мнемоническое правило для составления этой матрицы следующее. В первом столбце записываются все нечетные коэффициенты характеристического уравнения, начиная с а1. Затем каждая строка матрицы дописывается последовательно коэффициентами с уменьшающимися номерами вплоть до а0, после чего дописываются нули так, чтобы общее количество элементов в строке равнялось n. В результате в главной диагонали определителя оказываются последовательно все коэффициенты, кроме а0. Например, третья строка матрицы должна начинаться с нечетного коэффициента а5 и выглядеть следующим образом:
, (6.9)
Условия устойчивости заключаются в требовании положительности определителя Гурвица и всех его диагональных миноров.
Развернем критерий Гурвица для нескольких конкретных значений n.
Для n=1
и условия устойчивости сводятся к неравенствам:
.
Для n=2
;
.
Условия устойчивости: a0>0; a1>0; a2>0. Система на границе устойчивости, если а1=0 или а2=0. Звено с передаточной функцией 
устойчиво, если перед всеми членами стоит знак плюс и находится на границе устойчивости, если Т2=0.
Для n=3
;
Условия устойчивости: a0>0; a1>0;
;
.
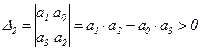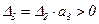Для n=4
;
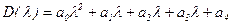Условия устойчивости: a0>0; a1>0;
;
;
.
Очевидно, что условия устойчивости опять сводятся к требованию положительности всех коэффициентов. То же самое можно сказать и для системы n -го порядка. Поэтому анализ устойчивости надо начинать с проверки этого простого необходимого, но недостаточного условия устойчивости.
Условия устойчивости, получаемые из критерия Рауса-Гурвица, усложняются с ростом порядка системы. Так, например, для уравнения 5-го порядка надо сделать около 60-ти умножений. Поэтому используют специальные приемы, например таблицы Рауса. Для систем 4-го и выше порядка целесообразно использование частотных критериев устойчивости.
Рассмотрим пример анализа устойчивости системы управления, принципиальная схема которой приведена на рисунке 6.3. Предположим, что контур напряжения оптимизирован, т.е. передаточная функция регулятора напряжения
, (6.10)
Тогда передаточная функция замкнутого контура напряжения будет иметь вид:
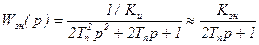, (6.11)
Здесь 
.
В данном случае пренебрегаем величиной 2Tп2p2, полагая что Tп<<1.
Если Tм>4Tэ, то передаточная функция двигателя по управляющему воздействию может быть представлена в виде:
, (6.12)
где 
.
Учитывая (6.11), (6.12), а так же считая, что гибкая отрицательная обратная связь по току двигателя отключена, т.е. Ki=0, получим структурную схему, представленную на (рисунке 6.3). Этой структурной схеме можно поставить в соответствие передаточную функцию
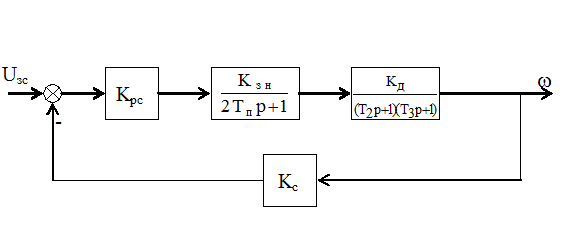
Рисунок 6.3 Структурная схема САРС
,
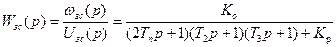(6.13)
где 
; 
.
Выражению (6.13) соответствует характеристический полином
,
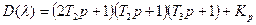т.е.:
.
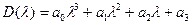Здесь:
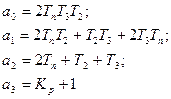; (6.14)
Условие устойчивости, как показано выше, для n=3 сводится к следующим неравенствам:
Первые четыре неравенства не представляют особого интереса, т.к. из них следует только лишь условие положительности постоянных времени и коэффициентов передачи.
Последнее неравенство налагает реальные ограничения на параметры системы. Его удобно переписать в виде:
. (6.15)
Это неравенство показывает, что устойчивость системы нарушается при определенном значении коэффициента усиления разомкнутой системы. Его предельные значения определяются постоянными времени системы. Согласно (6.15), это критическое значение
, (6.16)
Отсюда: величина коэффициента усиления регулятора скорости не должна превышать величины
, (6.17)
Допустим, что рассматриваемая САУ имеет следующие параметры:
Uгн=Uдн=830 В; Iн=8700 А; Rэ=0,006 Ом; nн=60 об/мин; Тэ=0,045 с-1; Тм=0,18 с-1; Kг=10; Kтп=40; Тп=0,02 с; Тг=4,4 с; Wрн(р)=Kрн=9; Ku=0,03.
Определим KЕ, Т2, Т3.
,
где 
.
Тогда 
.
В нашем случае Тм>4Тэ, поэтому двигатель можно представить двумя последовательно соединенными апериодическими звеньями, т.е.
,
где 
.
Из (6.16) следует
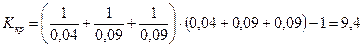(6.18)
. (6.19)
