Часто требуется полное устранение статизма системы. Для того, чтобы выяснить пути полного устранения статизма, обратимся вновь к общему выражению для yст, полученному через передаточную функцию путем подстановки в нее p=0:
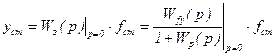, (5.15)
При наличии fст статическое отклонение будет отсутствовать, если при p=0 выражение Wз(p) обратится в нуль. Это возможно в двух случаях: если Wfy(0)=0 или если W(p)=¥. Первый путь реализуется введением компенсирующего воздействия по возмущению и рассматривался нами ранее при анализе систем с принципом управления по возмущению (1.21¸1.23). Второй путь реализуется введением в систему интегрирующего звена, т.е. переходом к так называемой астатической системе управления. Такую систему можно получить, если ввести в рассматриваемую статическую САУ интегрирующее звено так, чтобы оно находилось вне участка системы от места приложения f до y, т.е. чтобы его передаточная функция не входила в Wfy(p). В этом случае, как следует из (5.15), статическое отклонение yст будет равно нулю, так как при конечном значении Wfy(0)=Kfy имеем Wp(0)=¥ из-за наличия в знаменателе Wp(p) множителя p, обязанного своим появлением передаточной функции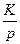 
интегрирующего звена.
Наличие интегрирующего звена между точками нахождения f и y, т.е. в составе передаточной функции Wfy(p), не устраняет yст. Это легко показать, используя выражение (5.15).
Таким образом, для получения астатической САУ достаточно в замкнутый контур регулирования ввести интегрирующее звено. В связи с этим, интегрирующее звено часто называют астатическим. Астатическим называется элемент, у которого при постоянном входном воздействии сигнал на выходе в установившемся режиме непрерывно растет с постоянной скоростью, ускорением и так далее.
Вернемся к нашему примеру. Если вместо усилительного звена поставить ПИ-регулятор с передаточной функцией
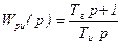, (5.16)
то статизм системы станет равным нулю. Структурная схема такой системы представлена на рисунке 5.4.
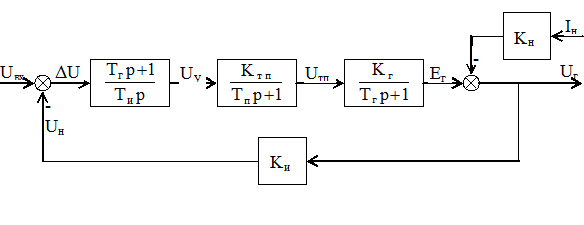
Рисунок 5.4 Структурная схема астатической системы автоматического регулирования напряжения генератора
Передаточная функция замкнутого контура относительного возмущающего воздействия в виде
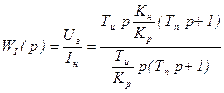, (5.17)
откуда следует, что по окончании переходного процесса отклонение выходной величины Uг равно 0, т.е. система астатическая относительно возмущающего воздействия.
Записывая передаточную функцию относительно входной величины Uвх, получим
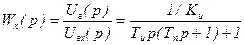, (5.18)
Из выражения (5.18) следует, что система статическая относительно управляющего воздействия.
Таким образом, одна и та же САР может быть статической по отношению к какому-либо возмущающему воздействию и астатической по отношению к управляющему воздействию, и наоборот.
