Середні значення випадкової величини мають ту ж розмірність, що й сама випадкова величина, і обчислюються:
Ø середня арифметична для оцінки математичного очікування випадкової величини - функція СРЗНАЧ;
Ø середня геометрична для оцінки середніх темпів росту, знаходження значення, рівновіддаленого від інших значень - функція СРГЕОМ;
Ø середня гармонійна для оцінки середньої суми зворотних величин - функція СРГАРМ.
Ø Основні характеристики випадкової величини:
Ø число значень – функція СЧЕТ;
Ø сума значень - функція СУМ;
Ø дисперсія - характеризує розкид значень випадкової величини біля середньої арифметичної, розмірність дисперсії - розмірність випадкової величини у квадраті. Розрізняють дисперсію по вибірковій сукупності значень випадкової величини - функція ДИСП і по генеральній сукупності - функція ДИСПР;
Ø стандартне відхилення має ту ж розмірність, що й випадкова величина. Розрізняють стандартне відхилення по вибірці - функція СТАНДОТКЛОН), стандартне відхилення по генеральній сукупності - СТАНДОТКЛОНП;
Ø середній модуль відхилень, нівелюється знак відхилення від середнього, є показником сили варіації - функція СРОТКЛ;
Ø довірчий інтервал для середнього значення випадкової величини - функція ДОВІРИТЬ;
Ø середня квадратична помилка середнього - обчислюється як відношення СТАНДОТКЛОН до кореня квадратному із числа елементів вибірки;
Ø мінімальне значення випадкової величини - функція МІН;
Ø максимальне значення випадкової величини - функція МАКС;
Ø інтервал - розмах варіації, рівний різниці максимального й мінімального значень випадкової величини;
Ø порядкове найбільше значення випадкової величини - функція НАЙБІЛЬШИЙ;
Ø порядкове найменше значення випадкової величини - функція НАЙМЕНШИЙ
Міра взаємного розташування даних у масиві значень характеризується за допомогою функцій МОДА, КВАРТИЛЬ, МЕДІАНА, ПЕРСЕНТИЛЬ, ПРОЦЕНТРАНГ.
Мода - найбільш імовірне значення випадкової величини. При симетричному розподілі щодо середнього мода збігається з математичним очікуванням. Якщо значення випадкової величини не повторюються, мода відсутня.
Безліч значень випадкової величини ділиться на 4 рівні частини по числу змінних - квартилі. У квартилях значення змінних упорядковані по зростанню. Указується номер частини (квартиля) і відповідне початкове значення змінної певного квартиля:
Ø 0 - мінімальне значення;
Ø 1 - значення 25-го персентиля (персентиль - одна сота частка масиву значень випадкової величини);
Ø 2 - значення 50-го персентиля або медіани;
Ø 3 - значення 75-го персентиля;
Ø 4 - максимальне значення.
Форма розподілу випадкової величини характеризується значеннями асиметрії й ексцесу - функції СКОС і ЕКСЦЕС відповідно.
Асиметрія служить для оцінки симетричності розподілу випадкової величини щодо середньої. Якщо асиметрія - позитивне число, розподіл має зрушення убік позитивних значень, інакше - убік негативних значень.
Ексцес є характеристикою гостро конечності або згладженості кривої розподілу щільності ймовірності випадкової величини. Ексцес дорівнює нулю для нормального розподілу, позитивний для гострих і негативний для згладжених у порівнянні з нормальною щільністю розподілу.
Пакет аналізу забезпечує найбільш швидкий засіб формування описової статистики. Команда меню Сервіс? Аналіз даних викликає діалогове вікно. Інструменти аналізу, у якому вибирається Описова статистика. Вихідні дані для аналізу розташовуються в осередках рядків або стовпців таблиці й можуть мати мітки. Для вхідного інтервалу вказується орієнтація - по рядках або стовпцям, наявність мітки рядка або стовпця.
Описова статистика обчислює з показники: середнє, стандартна помилка, медіана, мода, стандартне відхилення, дисперсія вибірки, ексцес, асиметричність, інтервал, мінімум, максимум, сума, рахунок, k-й найменший, k-й найбільший, довірчий інтервал для заданого рівня надійності. Результати описової статистики виводяться в зазначене місце (поточний аркуш, інший аркуш, нова книга).
Приклад 1
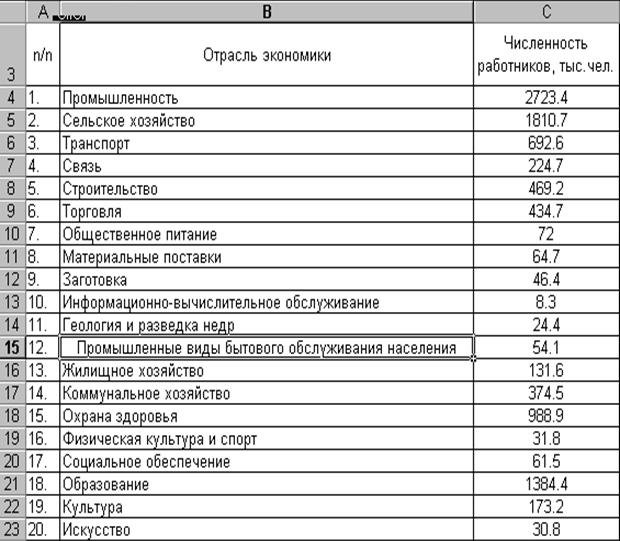
Застосувати методи описової із для аналізу кількості працівників галузей економіки України, яким нарахована заробітна плата за березень 2006 року. Розмірність масиву вихідних даних 20 елементів (табл.1).
Таблиця 1
Чисельність працівників галузей економіки України, яким нарахована заробітна плата за березень 2006 р.
Ø Послідовність дій
Ø 1. Створити робочу книгу за допомогою команди меню Файл? Створити.
Ø 2. Перейменувати перший аркуш за допомогою команди меню Формат? Аркуш? Перейменувати, в аркуш - Статистика1.
Ø 4. Розмістити вихідні дані в стовпцях і вказати їхньої назви.
Ø 5. За допомогою команди меню Сервіс? Аналіз даних викликати діалогове вікно Аналіз даних Вибрати інструмент аналізу? Описова статистика Вказати параметри описової статистики (рис 1,2):
Ø ў вхідний інтервал - блок осередків, що містить число працівників, включаючи назви стовпця, групування по стовпцях, указати наявність міток у першої строки;
ў вихідний інтервал - Новий робочий аркуш;
ў указати Підсумкова статистика; рівень надійності - 95%; обчислити k-й найменший - 2; k-й найбільший - 2.
ў із кнопку ОК.
ў З новий аркуш в аркуш Підсумок1.
6. Закрити файл зі збереженням за допомогою команди меню Файл? Закрити. Привласнивши йому ім'я Аналіз-номер групи. Наприклад Аналіз-351.

Рис. 1 Перше діалогове вікно Аналізу даних

Рис.2 Друге діалогове вікно Аналізу даних
Таблиця 2
Результати розрахунків
| Показник | Значення |
| Середнє | 490,095 |
| Стандартна помилка | 161,6843 |
| Медіана | 152,4 |
| Мода | #Н/Д |
| Стандартне відхилення | 723,0741 |
| Дисперсія вибірки | 522836,2 |
| Ексцес | 4,1284 |
| Асиметричність | 2,070713 |
| Інтервал | 2715,1 |
| Мінімум | 8,3 |
| Максимум | 2723,4 |
| Сума | 9801,9 |
| Рахунок | |
| Найбільший(2) | 1810,7 |
| Найменший(2) | 24,4 |
| Рівень надійності(95,0%) | 338,4092 |
Вправа 1.
Таблиця 3
Кількість і заробітна плата працівників зайнятих у галузях економіки
| Галузь економіки | Середньо облікова чисельність штатних працівників, тис.чол. | Заробітна плата нарахована в середньому за місяць на один штатного працівника, грн. | ||
| 2005г. | 2006г. | 2005г. | 2006г. | |
| Промисловість | 4338.5 | 4323.6 | 173.2 | 176.14 |
| Сільське господарство | 2916.5 | 2914.1 | 69.3 | 70.83 |
| Лісове господарство | 128.9 | 104.2 | 109.7 | 112.25 |
| Рибне господарство | 29.6 | 23.9 | 79.3 | 81.35 |
| Транспорт | 963.2 | 962.5 | 177.3 | 180.33 |
| Зв'язок | 269.4 | 207.6 | 209.55 | |
| Будівництво | 849.8 | 827.7 | 153.5 | 156.31 |
| Торгівля | 597.1 | 567.7 | 120.1 | 123.91 |
| Громадське харчування | 131.6 | 102.4 | 67.1 | 70.02 |
| Матеріальні поставки й збут | 93.5 | 85.5 | 160.1 | 163.65 |
| Заготівля | 71.6 | 64.8 | 157.3 | 157.67 |
| Інформаційно-обчислювальне обслуговування | 12.2 | 10.2 | 189.1 | 190.68 |
| Геологія й розвідка надр, геодезична й гідрометеорологічна служба | 40.3 | 159.0 | 160.13 | |
| Промислові види побутового обслуговування населення | 79.3 | 76.8 | 68.9 | 70.88 |
| Житлове господарство | 169.5 | 153.7 | 132.1 | 134.38 |
| Комунальне господарство | 455.4 | 445.4 | 189.8 | 192.1 |
| Непромислові види побутового обслуговування населення | 35.3 | 29.1 | 97.5 | 98.41 |
| Охорона здоров'я | 1201.8 | 1175.6 | 120.0 | 122.71 |
| Фізична культура й спорт | 59.7 | 34.3 | 136.6 | 139.53 |
| Соціальне забезпечення | 95.4 | 72.1 | 101.0 | 103.36 |
| Утворення | 1576.1 | 1554.4 | 122.1 | 126.43 |
| Культура | 217.3 | 208.9 | 95.9 | 97.36 |
| Мистецтво | 45.2 | 42.1 | 115.2 | 117.44 |
| Наука й наукове обслуговування | 239.8 | 213.9 | 112.5 | 117.35 |
| Фінансування, кредитування й страховання | 162.7 | 314.9 | 319.53 | |
| Апарат органів державного й господарського керування, органів керування кооперативних і громадських організацій | 587.1 | 573.8 | 180.2 | 183.46 |
Застосувати методи описової статистики для аналізу кількості й заробітної плати працівників галузей економіки України. Розмірність масиву вихідних даних 26 елементів.
Дані таблиці3 розмістити на аркуші 2. Аркуш2 перейменувати в аркуш Статистика2. Таблиці результатів розмістити на новому аркуші, давши йому назва Підсумок2. Зрівняєте результати аналізу даних за 2005 і 2006 роки.
ПРАКТИЧНА РОБОТА 2
ОДНОФАКТОРНИЙ ДИСПЕРСІЙНИЙ АНАЛІЗ
Дисперсійний аналіз - це особливий прийом установлення кількісної залежності між досліджуваними ознаками сукупності. При дослідженні залежностей однієї з найбільш простих є ситуація, коли можна вказати тільки один фактор, що впливає на кінцевий результат, і цей фактор може приймати лише кінцеве число значень (рівнів). Такі завдання називаються завданнями однофакторного аналізу. Однофакторний дисперсійний аналіз використається для перевірки гіпотези про подібність середніх значень двох або більше рівнів фактора, що належать однієї й тієї ж генеральної сукупності. Цей метод поширюється також на тести для двох середніх (до яких з також t - критерій).
Приклад 2
Розглянемо статистичну сукупність, що розбита на групи (рівні) по регіонах України. Наприклад, фірма продає свої товари в різних регіонах України, має дані про обсяги продажів у цих регіонах по окремих торговельних крапках фірми. Менеджери фірми хочуть внести зміни в організацію регіонального менеджменту. Насамперед необхідно виконати статистичний аналіз, чи є розходження в середніх обсягах продажів по даних регіонах і чи є вони випадковими або невипадковими, істотними або несуттєвими.
Найпоширенішим і зручним способом подання подібних даних для однофакторного дисперсійного аналізу є таблиця (табл.4). Для розрахунків можна використати Сервіс - Аналіз даних - Однофакторний дисперсійний аналіз. Якщо для дослідження прийняті лише два середніх значення, то можна використати функцію ТТЕСТ у Майстру функцій.
При використанні пакета "Аналіз даних" необхідно згрупувати дані певним чином. Наприклад, дані для кожного з п'яти регіонів представлені в окремому стовпці, у першому рядку якого втримується назва регіону.
Таблиця 4.
Обсяги продажів продукції фірми по регіонах України, грн..
| A | B | C | D | E | |
| Север | Северо-запад | Восток | Юг | Юго-запад | |

Рис. 3 Діалогове вікно "Однофакторний дисперсійний аналіз"
Ø Порядок дій:
Ø 1. Відкрити файл Аналіз. Додати новий аркуш. Перейменувати його й давши ім'я Дисперсія. Розмістити на аркуші Дисперсія дані таблиці 4.
Ø 2. На мал.3 показане діалогове вікно Однофакторний дисперсійний аналіз, у яке необхідно ввести інформацію для проведення аналізу, а саме встановити наступні параметри:
Ø ў клацнути в поле Вхідний інтервал і ввести діапазон осередків А1:Е9;
Ø ў установити перемикач по стовпцях у групі Групування;
Ø ў установити прапорець Мітки в першому рядку;
ў з у поле Альфа значення 0,05, установлене за замовчуванням, або змінити його на інше значення в діапазоні від 0 до 1;
ў визначитися параметри висновку- Новий робочий аркуш.
3. Новий аркуш разом перейменувати давши йому ім'я Підсумок3.
Результати розрахунку представлені в таблиці 5.
Таблиця 5
Результати розрахунку
| Однофакторный дисперсионный анализ | ||||||
| ИТОГИ | ||||||
| Группы | Счет | Сумма | Среднее | Дисперсия | ||
| Север | 1307617.286 | 1.74169E+12 | ||||
| Северо-запад | 2103706.6 | 2.25978E+11 | ||||
| Восток | 2.56978E+12 | |||||
| Юг | 455198.6667 | |||||
| Юго-запад | 781815.625 | 1.80068E+11 | ||||
| Дисперсионный анализ | ||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Между группами | 1.1397E+13 | 2.84937E+12 | 3.067431112 | 0.037689179 | 2.816705091 | |
| Внутри групп | 2.0436E+13 | 9.28911E+11 | ||||
| Итого | 3.1834E+13 |
Перша частина результатів (таблиця "Підсумки") являє собою звіт описової статистики для кожного регіону: кількість спостережень (рахунок), сума, середнє й дисперсія обсягу продажів у даному регіоні (див. лабораторну роботу 1).
Для розуміння другої частини таблиці необхідно згадати деякі поняття математичної статистики, а саме, групова дисперсія, внутрігрупова дисперсія, межгрупповая дисперсія й загальна дисперсія.
Групова дисперсія характеризує варіацію значень кожної групи щодо її середнього значення.
Внутрігруповою дисперсією називають среднеарифметическую групових дисперсій, зважену на обсяг груп (частоту значень).
Межгрупповая дисперсія - це дисперсія групових середніх щодо середнього значення всієї сукупності.
Загальна дисперсія характеризує варіацію, викликану дією всіх рівнів фактора. Вона обчислюється за індивідуальним значенням всієї сукупності щодо її середнього значення. Загальна дисперсія дорівнює сумі внутрігрупової й межгрупповой дисперсій.
Друга частина (таблиця "Дисперсійний аналіз") містить виведену інформацію, тобто дані, що ставляться до питання про значимості спостережуваних результатів продажів у розрізі міжгрупових і внутрігрупових показників. У ній представлені:
ў Df - число ступенів волі (незалежні значення);
ў SS - сума квадратів відхилень;
ў MS - дисперсія, розраховується як відношення SS/Df;
ў F - відношення дисперсії регресії до дисперсії залишку;
ў Значимість F - рівень значимості, розраховується як
МSрегрессия/МS0статок.
Дисперсійний аналіз дозволяє оцінити ймовірність появи розбіжності між фактичними й передбачуваними значеннями за умови, що спостережувані розходження викликані випадковими подіями. У нашому випадку рівень імовірності (Р-Значение) дорівнює 0,0377. На підставі цього можна з висновок, що розходження в обсягах продажів, швидше за все, носять невипадковий характер і викликані конкретними обставинами (імовірність становить 96%), а ймовірність випадкових обставин дорівнює всього 4%. Виходить, при зміні маркетингової політики фірми необхідно враховувати регіональний фактор і варто більш детально вивчити розходження в демографічних і економічних умовах регіонів і ступінь їхнього впливу на обсяг продажів.






