Выбор вида ур-ия регрессии с использ-ем теста Бокса-Кокса

Исп-ие нелин-ых ур-ий для построения ур-ия регрессии значит-но повышает универс-сть регр-го анализа, но и усложняет задачу исслед-ля, т.к. усложняется проблема спецификации ур-ия регрессии. Если мы имеем дело с парной регрессией, то вид ур-ия м.б. решен (выбран) путем построения графика зависимости у = f(x) и по виду этого графика можно дост-но просто выбрать ур-ия. Однако в случае множ-ой регрессии такой подход практич-ки невозможен. В этом случае часто задача решется путем подбора подходящей функции и в качестве критерия оптим-ти используют коэф-т множ-ой детерминации R², иногда сумма квадратов отклонений. Такой подход неправомерен, если сравниваются принципиально различ-е функц-ые зависимости. Н-р: лин-ая аддитивная модель (1) мультипликтивная модель (2)

Использовать для срав-ия этих моделей сумму кавдратов отклонений невозм-но, т. к. lny_i ≠ y_i, а значит-но < его

(3)

Величина R² также не может быть использ-на, хотя она и безразмерна, т. к. она относ-ся к разным понятиям. В (1) она объясняет дисперсию у, объясн-ую дисперсией факториальных приз-ов (х₁ и х₂). Во (2) она объясняет дисперсию lny, вызванную дисперсией ln х₁ или ln х₂. В тех случаях, когда R² у одной модели значит-но >, чем у другой, тогда можно обоснованно осущ-ть выбор в пользу этой модели. Однако в тех случаях, когда R² одной и др. модели соизмеримы др.с другом, то проблема выбора усложняется. В этом случае предлагается для выбора исп-ть тест Бокса-Кокса (это в общем случае). Для сравнения моделей (1) и (2) Пол Зарембко предложил упрощение теста Бокса-Кокса в 1968г. Суть теста в этом сл. след-ая:

1) исход-ые данные по у исп-ся для вычисления средней геометрической

2) значение у персчит-ся с исп-ем

3) исп-ие нов. знач-я у находим параметры (оценки) ур-ия (1). А исп-уя ln y’из ур-ия (3) нах-ся оценки а_о,β₁,β₂.Для этих двух моделей (1) и (3) нах-ся сумма квадратов отклонений. Эти суммы являются сопоставимыми и след-но та модель, которая дает меньшую сумму квадратов отклонений и признается лучшей.

4) для того, чтобы окончат-но решить вопрос, что действительно одна из моделей дает лучшее соответ-ие, рассчит-ся пок-ль: 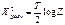, где Т-число набл-й (n), Z-отнош-е ∑ кв. отклонений в 1 и 2 ур-ии. . Х²_расч. сравнив-ся с табличным. Данное стат. распределение им. одну степень свободы и разное знач-е уровня значимости, если Х²_расч. > Х²_табл. при 5 %-значимости, то действ-но одна из моделей сущ-но лучше другой.

13.1 Общая характеристика временных рядов. Трендовые модели.

Динамич. процессы, происх-ие в эк-их системах чаще всего проявляются в виде ряда послед-но располож-ых в хронолог-ом порядке знач-ий того или иного пок-ля, кот. в своих изменениях отражает ход развития изучаемого явления. Эти знач-я пок-ей могут служить основой для разработки прикладн. моделей особого вида, наз-ых трендовыми моделями. Послед-ть наблюдений одного пок-ля, упорядоч-ая в завис-ти от послед-но возраст-их или убывающих знач-ий др. показ-ля наз. динамическим рядом. Если в кач-ве приз-ка, в завис–ти от кот-го проис-ит упорядочеие, берется время, то такой динамич. ряд наз. временным рядом. Состав-ми элем-ми радов динамики явл. цифровые значения пок-ля, наз-ые уровнем этих радов и моменты или интервал времени, к кот. относ-ся эти уровни. Временные ряды образованные пок-ми. харк-ми эк. явления на опред. моменты времени над. моментными. Если уровни временного ряда образ-ся путем агрегирования за опред-ый промежуток времени, то такие рады наз-ся интервальными врем. Рядами. Врем. Ряды могут быть образованы как из абсолютных знач-й эк. пок-ей, так и из средних относит-ых величин. Эти ряды наз. производными рядами. Под длиной врем. ряда поним-ся время, прошедшее от начала момента набл-ия до конечного. Если во врем. ряду прояв-ся длит-ая тенденция изм-ия эк. пок-ля, то считается, что в этом имеется тренд. След-но под трендом поним-ся изменение, опред-ее общее направ-е развития, т. е. осн. тенденция врем. ряда. След-но, эк-ко-мат-ая динамич-ая модель, в кот. развитие эк. системы отраж-ся через тренд ее осн. показ-ей наз. трендовой моделью. Отличие врем. эк. радов от простых стат. совокуп-ей закл-ся прежде всегов том, что послед-ые знач-я уровня временного ряда зависят друг от друга, т. е. имеется существенная автокорел-ия между уровнями ряда (не остатков, а х). В связи с этим выводы и формулы ТВ и МС могут исп-ся с большей осторожностью. Любой врем. ряд эк. пок-ей можно разложить на 4 составл-ие: , где Т-тренд, S-сезонная сост-ая, С-циклич-ая сост-ая, -случ-ая сост-ая. При построении трендовых моделей необходимо, чтобы дан. Модельсущ-ым образом отражала изменения систематич-их компонент врем. ряда. (Т, S, C). Случ. сост-ая () для адекватных моделей должна подчиняться 4 св-ам Гаусса-Марка (2 лаб. Работа):1) случай-ть колеб-й; 2) мат. ожидание = 0; 3) норм-ый закон распр-ия; 4) независ-ть. - трендовая модель.