В кач-ве примера рассм.спрос на автомобили в завис-ти от располагаемого дохода ур-ие регрессии запишем в сл.виде: 
; y-спрос на авто; x-располаг.доход
Предполагается, что со временем доход растет. Проводится анализ с 1963 по 1983. В 1974 наблюдалось резкое снижение спроса на авто из-за повышения цены на бензин. (график)
Чтобы учесть в одном ур-ии: 
Если δ считать отриц.величиной, то с 1963 по 1974г.,D=0; а с 1974 по 1983г., D=1.
Использование сезонных фиктивных переменных.
При исп-ии данных вр.рядов зачастую вместо годовых данных исп-ют квартальные пок-ли это позволяет существенно увеличить кол-во наблюдений. Однако на эти данные сущ-ое влияние оказ.сезонный фактор.Н-р, расходы потребителей на газ и электричество растут во времени(от года в год), но и изм.сущ-но от сезонов года. Для учета этого исп-ем след.ур-ие регрессии: 
y- потребление (в руб.), t-время, D2,D3,D4-фиктив переменные
За базовый период взят 1-ый квартал. В этом сл.все фиктив.переменные = 0
Если наблюдение относится ко 2-му кварталу, то D2=1, D3=0, D4=0
Если наблюдение относится ко 3-му кварталу, то D3=1, а ост. = 0
Если наблюдение относится ко 4-му кварталу, то D2=0, D3=0, D4=1
Обычно 
имеет отриц.значение. (график)
Это сезонное отражение изменения потребления газа и электричества за год.
Фиктивные переменные для коэф-та наклона ур-ия регрессии.
Любые примеры обеспечивали интерпретацию сдвига графиков (вверх,вниз) при изм-ии кач-го признака. При этом предполагалось, что наклон графика не зависит от кач-го признака, что не всегда верно. В связи с этим введем фиктивную переменную для коэф-та наклона, назыв-ый иногда фиктив.переменной взаимодействия. В любом ранее примере с рождением первенца/не первенца ур-ие регрессии имело вид:: 
D=0- если первенец; D=1-если не первенец
Введем дополнительную фиктивную переменную для коэф-та наклона графика:
; 
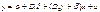
D1=0, D2=0, если первенец 
D1=1, D2=1, если не первенец
Доугерти провел исслед-ие и получил:
Если первенец=(3363-4х)гр. Если матери курят, (график)
Если не перв.=(3410-12х)гр. то вес меньше
Тест Чоу.
Иногда выборки наблюдений состоят из двух или более подвыборок и необходимо решить вопрос: «сделать для каждой подвыборки отдельное уравнение регрессии или сделать одно общее уравнение регрессии?»
Для подвыборки А: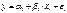 
Для подвыборки В: 
Для подвыборки А+В: 
Обозначим суммы квадратов остатков для регрессии подвыборок 
, и 
, и 
(сумма квадратов отклонений для регрессии А+В на участке А), и 
(сумма квадратов отклонений для регрессии А+В на участке В)
Естественно предположить, что 
, а 
Следовательно, 
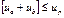
Up – сумма квадратов отклонения для регрессии (А+В). В пределе 
. Это будет достигаться при совпадении коэффициентов уравнения регрессии (Объединенной регрессии и регрессии подвыборок). Таким образом можно сказать, что имеется уличшение качества уравнения регрессии равное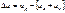 
за счет представления уравнения регрессии в виде двух уравнений регрессии.
Однако в этом случае уменьшается число степеней свободы, т.к. в первом случае для объединенной регрессии мы имели число степеней свободы k=n-p-1, где р – число неизвестных.
Если мы берем для двух уравнений регрессии (А+В), то k2=n-2p-2.
Кроме того во втором случае остается необъясненной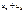 
поэтому необходим критерий, который помог бы однозначно решить вопрос: «эффективно ли улучшение качества уравнения, получаемое за счет использования двух уравнений регрессии, по сравнению с использованием одного уравнения»
Для решения этого вопроса используется тест Чоу, который предполагает вычисления критерия Фишера по формуле:
Где в числителе записано улучшение качества уравнения, деленное на использованные степени свободы, а в знаменателе необъясненная дисперсия результативного признака, деленное на число оставшихся степеней свободы.
Данные расчетные значения критерия Фишера сравнивается при 5% уровне значимости нулевой гипотезы.
Нулевая гипотеза: в ген. Совокупности улучшение качества за счет использования двух уравнений регрессии равно 0.
Табличное значение Fp находится из таблицы со степенями свободы 
; 
Если Fp меньше Fтабл, то нулевая гипотеза отвергается и считается, что улучшение качества за счет использования двух уравнений регрессии существенно, т.е. имеет смысл их использовать.
