Задачей регрессионного анализа явл.нахожд-е такой кривой ур-я регрессии, кот.наилучшим обр.подходила к имеющимся фактическим данным. В больш-ве случаев исследов-ли пытаются найти параметр лин.алгебр.ур.вида: у=а0+а1х1+а2х2+…архр.
Для этого ур-я разраб.надежные стат.методы оценки парам-ров и легко дать эк.интерпритацию парам.ур.регрессии. И в этом случае возн.вопр.о кол-ве использ.фак-ров. Матем.кол-во фак-ров можно увел.до числа наблюдений и найденное при этом ур-е будет иметь кривую, кот.пройдет все точки наблюдения. В этом случае нах-ся не закономерность развитий явлений, а сами эти случайные колебания, т.е.познават.ценность модели будет близка к 0.
Эта зад.реш-ся путем нахождения коэф.множеств., парной и частной корреляции. Вычисл-е основано на законе сложения дисперсии. Для ур-я у=а0+а1х1+а2х2+…архр линейный случай:
Коэф.парной и частной коррел., коэф.эластичности.
После линейного ур-я регрессии, в рез-тате расчетов нах-ся практически теоретич.завис-ть результирующ.признака от факторов аргумента у=а0+а1х1+а2х2+…архр. Эта зад.закл.в определении силы, с кот.найден завис.проявл.среди многообр.нарушающих ее возд-вий. Данная задача распадается на 2е: 1)определ-ся степенью возд-я всех аргументов на результир.показ-лях; 2)определ-ся степень возд-я каждого аргум.на результир.показ-лях.
Коэф.парной коррел.:
показ.устойч.стат.связь м/у х и у.
Коэф.порной коррел.правильно отражает силу фактора по у при условии, что в стат.данных отражено изм-е у и х при постоян.значениях др.фак-ров, влияющих на у. Данное обстоят-во мож.иметь и положит.обстоят-во, т.к.этот коэф.коррел.фактич.отражает влияние всей совок-ти фак-ров, изм-щихся вместе с изучаемым фак-ром в том же направл. Т.обр.исслед-ль, включив в ур-е регрессии фактор хj учитывает в этой модели влияние на у целой совок-ти фак-ров, иногда даже не зная об этом.
Для оценки чистого влияния на у конкр.фактора исп-ся коэф.частной корелл.:
В практических прилож-ях реал.оценку фак-ров определяет коэф.эластичности:
Коэф.множественной коррел.и детерминации.
После линейного ур-я регрессии, в рез-тате расчетов нах-ся практически теоретич.завис-ть результирующ.признака от факторов аргумента у=а0+а1х1+а2х2+…архр. Реш.корреляц.зад.на фоне анализа, кот. позволяет решить как изм.результирующий признак при изменении части аргументо, кот.вкл.в модель при условии, что остальные аргум.нах-ся на одном и том же ср.уровне.
Отнош.дисперсий теор.к общей – это коэф.множеств.детерминации:
Коэф.множеств.корреляции показ.тесноту линейной корреляц.связи фак-ров с у: R= 
. Если R=1, то мы имеем не кореляц.связь, а функциональную. Если R=0, то стат.устойчивых связей нет 0<=R>=1.
Критерий Фишера.
Критерий Фишера характ-ет отношение общей дисперсии зависимой и остаточной переменной:
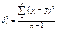
Задаем уровень значимости нулевой гипотезы, находим v1 и v2 и по табл.критич.знач.находим на их пересечении критич.знач-е:
В генерал.совок-ти все коэф.при факторах (в1 и в2)=0, а0=у
y=a0 +b1x1 +b2x2+ε; у=а0=у
Fт>Fp – соглашаемся, если наоб.- опровергаем нулевую гипотезу.
tp>tт – нулевая гипотеза отклоняется
ν=n-p-1.
Вячисл-е критич.знач-я t-критерия позволяет произвести оценку доверительного интервала изм-я данного парам-ра:
Критерий Стьюдента.
Для проверки значимости коэффициентов парной корреляции используют t-критерий Стьюдента. Для этой цели требуется найти для каждого коэффициента парной корреляции значение t-критерия Стьюдента, который рассчитывается по формуле:
где r – значение коэффициента парной корреляции; n – число наблюдений (n = 20).
Затем сравним tф для каждого коэффициента парной корреляции с t-критическим (табличное значение) для 5 % уровня значимости (двустороннего) и числа степеней свободы v = n - 2.
Если tф > tкр, то найденный коэффициент парной корреляции признается значимым. В модель включаются только те факторы, которые имеют коэффициент парной корреляции ryxj > 0,5. В случае, если между самими факторами коэффициент парной корреляции ryixj >= 0,8, для избежания мультиколлинеарности, в модель включается только один фактор, тот у которого больше ryixj.
