Наиб. лучший способ устранения – это опред-ть фактор, кот.вызывает авт-цию остатков и вкл.его в ур-ие регрессии. Однако, данный способ очень часто не может быть реализован или в связи с незнанием этого фактора или трудностью его измерения.
Поэтому исп-ют др.способы. Допустимым имеем ур-е регрессии: уt = α+βxt+Ut (1); уt-1 = α+βxt-1+Ut-1 (2) умножим на ρ и отнимем от (1): yt-ρ*yt-1= α (1-ρ) + β(xt-ρt-1) + Ut – ρ*Ut-1 (3); у’t= α*γ+β*x’t+ήt (4).
Метод Прайса-Уинстена. Недостатком такого подхода явл.то, что в сист.ур-ний вида (4) отсутств.1ое наблюдение. Сниж-е кол-ва наблюдений приводит к уменьш.числа степеней свободы и соотв.к сниж-ю эффект-ти МНК оценки. Что особ.характ-но для ЭММ и это приводит к сниж-ю эффект-ти оценок, соизмер.со сниж.эффект., вызванной автокоррел.остатка. однако в сист.ур.вида (4) остатки не завис.др.от др., а значит остаток в (1) не завис.от др.остатков, т.е.не связан с ним. След-но, (1) ур.можно вкл.в сист.ур.вида(4). Однако при таком приеме 1ое наблюд-е будет иметь неоправданно большой вес среди др.наблюдений, особ.при большом знач.ρ.
Поправка Прайса-Уинстена. Для того, чтобы уравновесить след.наблюд.с последующим., необх.умнож.его на коэфф. k=√1-ρ² и в этом случае устраняется чрезмерное влияние 1го наблюд-я.
8.3.2. Метод Кокрана-Оркатта. Метод Хилдрета – Лу.
Метод Кокрана-Оркатта.
Данный метод исп-ся для устранения автокоррел.итерационный хар-тер и вкл.след.этапы: 1.оцениваем исходное регрессионное ур-е, т.е. находим λ и β.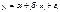 
2.вычисляем остатки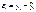 
3.находим:
4.исп-я найденный знач.строим сист.ур.вида: у’t= α*γ+β*x’t+ήt. 5.решив с пом.МНК сист.ур.находим новые оценки α и β. Затем повторяем этап 2.
Процесс повторяется до тех пор, пока не будет получена требуемая точность сходимости в оценках α и β
Метод Хилдрета – Лу.
В данном методе исслед-ль задает интервал изм-я величины ρ, допустим в пределах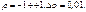 
Для каждого знач-я ρ производится оценка параметров α и β из ур-я: yt-ρ*yt-1= α (1-ρ) + β(xt-ρt-1) + Ut – ρ*Ut-1. Затем из полученных рез-татов выбир-ся такой, кот.дает минимальную стандартную ошибку для преобразованного ур-я. Исп-мые в этом ур-ии знач-я ρ, α и β принимаются за искомые. В сл., когда статистика Дарбина – Уотсона указ.на очень тесную положительную автокоррел., можно использ.упрощенную процедуру, в кот.принимается ρ =1. В этом сл.ур-е принимает след. вид: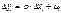 
9.2, 9.3 Мультиколлин-ть: способы ее обнаружения и устранения.
Мульт-сть – это коррелир-ть 2х или неск-ких объясняющих переменных в ур-ии регрессии. Оценка коэф-та ур-ия регрессии может оказаться незначимой не только из-за несущественности данного фактора, но и из-за того, что трудно разграничить воздействие на завершающую переменную 2-х или неск. факторов. Это обычно возникает в том сл.когда факторы линейно связаны м/д собой и меняются синхронно. Природу мульт-ти наиб.наглядно можно выявить на примере совершенной мульт-ти, т.е. в сл.если ф-ры функционально связаны друг с другом. Пусть ур-ие регрессии им.вид: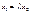 
(1) 
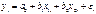(2)
Используя соотношение (1) и (2) можем переписать в сл.виде:
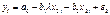или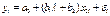 
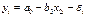
Используя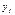 
и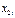 
МНК находим оценки: 
, но в этом сл.имеем одно ур-ие с 2-мя неизв-ми и следовательно найти значение оценок b1 и b2 невозможно.
В реальности имеем несовершенную мульт-ть, т.е. стахост.линейную связь м/у x1 и x2. Оценка этой связи находится путем расчета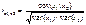 
. Чем ближе 
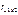к 1, тем ближе несовершенная мульт-ть к совершенной, и тем менее надежными будут оценки коэф-та регрессии при этих переменных.
Небольшое смещение ведет к большим изменениям признака. В эк.исследованиях счит.,что предельным значением коэф-та парной корреляции м/д двумя факторами д.б. 0,8. Устранение мульт-ти ведется путем искл-и одного из фак-ров из ур-ия регрессии. Искл-ют тот фактор, кот.: по мнению исслед-ля считается менее значимым; менее высокий коэф-т (r) с результат.переменной (y); более высокий r с др.факторами. Другие пути: изменить выборку
10. Обобщенный МНК и его исп-ие для оценки эфф-ти методов определения параметров уравнения регрессии.
Под обобщенным МНК будем понимать м-д опред-ия пар-ов ур-ия регрессии, кот.предполагает предварительное преобразование исх.данных, т.о. чтобы устранить гетероск-сть и автокор-цию остатков.
Согласно Доугерти, оценки ур-ия регрессии будут иметь желательные для МНК св-ва, если для преобразования ур-ий исп-ся истинные значения коэф-та ρ (показ-ля авток-ции остатков) и если сохранено первое наблюдение.
Учитывая данное положение можно сказать, что м-д Карно-Оркатто и Прайса-Уинстона работает лучше чем обычные МНК только для больших выборок.
Точность оценок ур-ия регрессии, опред-ых МНК, во многом зависят от закона изменения факториального признака и эту зависимость исследовали Парк и Митчелл. В своих исслед-ях они брали ур-ие регрессии вида: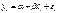 
, у кот.случ.составляющая имела авт-цию, подчиняется авторегрессионной схеме 1-го порядка: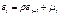 
В качестве исх. данных для каждого взято 3 вида зависимостей: 1. простоы временной тренд 2. ежегодные данные о ВНП США. В данной зав-сти на фоне случ.отклонений прослеживается опред.зависимость (слабый временной тренд) 3. ежегод.инф-ция о коэф-те исп-ния произв.мощностей США. В этой зависимости временной тренд отсутствует.
Случ.составл-ая генерируется генератором случ.цифр. Размер выборки = 20, и для кождой зависимости было сделано по 1000 экспериментов. Определялась относительная эфф-сть оценки как обратная величина отношения среднеквадратич. ошибки в эксперименте к соотв.ошибке при определении параметров с помощью обычного МНК. На основании повторного исслед-ия сделаны след.выводы: 1)выигрыш в эфф-сти, обеспечиваемый заменой обычного МНК на м-д Карнана-Оркатто (СО) или СО-PW (Прайс-Уинстон), то выигрыш в эфф-сти обеспечивается при наличии неярко выраженного тренда и большом значении ρ 2) в условиях сильного тренда, обычный МНК м.б.эфф-ым даже при высоких значениях ρ.
Исп-ие м-да СО в чистом виде значительно менее эфф-но, чем СО-PW когда данные подвержены сильному тренду. В этом сл.м-д СО работает хуже, чем обычный МНК, следовательно, всегда более целесообразно исп-ть м-д СО-PW, сохраняющий 1-ое наблюдение. Кроме того, исслед-ия показали, что при наличии авт-ции необх. исп-ть более высокие уровни значимости 0-гипотезы.
