Многие эк-ие явления более лучшим способом, чем лин-ые уравнения, описываются нелин-ми уравнениями. И в этом случае мы не можем применить к ним обычный МНК, и используем станд-ые подходы к оценке стат. надежности. В связи с этим встает задача по возможности привести нелин-ое уравнение к лин-му виду. В тех случаях, когда нелин-ть касается факториальных переменных, но не связана с нелин-тью коэф-ов ур-ия регрессии, нелин-сть обычно устраняется путем замены переменных:
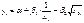Вводим нов. перемен.: 
и 
След-но 
, т. е. лин-ое ур-ие.
Во всех случаях, когда можно вычислить нов. перем-ую с использованием инф-ии об исход. перм-ой до опред-ия пар-ов ур-ия регрессии. Метод замены пер-ых решает поставл. задачи линеализацией ур-ия регрессии.
Линеаризация уравнения регрессии с использованием логарфмического преобразования (степенные и показательные функции).
В тех случаях, когда связь между фактор-ми перем-ми и результ-им приз-ом имеет вид степенного ур-ия (мультиколлин-ая функция) линеализация произв-ся путем логарифмирования исх. ур-ия.
Представление случайного члена в преобразованных нелинейных ур-ях регрессии.
(1)
(2)
Если 
в (1) удовл-ет четырем условиям случайности, т. е. мат. ожид-е =0, независимо др. от друга, то случ. Составляющая во (2) также будет удовл-ть этим усл-ям, и найденные из (2) с пом. МНК оценки параметров будут несмещ-ми, состоят-ми и эффектив-ми оценками. Если будем иметь ур-ие вида: 
(3), то случ. состав-ая должна входить как сомножитель.
(4)
Четырем усл-ям случайности должен удовл-ть lnδi, а само δi подчин.др. законам. Н-р, 
В получаемые с пом. МНК оценки состоятельные и эфектив-ые для ур-ия (4) и все стат. критерии справедливы для лин-го аддитивного ур-ия (4).
Определение параметров нелин-го ур-ия герессии, не приводимого к лин-му ур-ию.
Возьмем ур-ие: 
.Данное ур-ие не м. б. приведено к лин-му путем замены переменных или логарифмированием. Для оценки парам-ов данного ур-ия также используем метод минимизации суммы квадратов отклонений. Алгоритм нах-ия парам-ов α и b представим в виде послед-ти процедур:
1) примем некоторые правдоподобные исходн. знач-я α и b (α =1÷10, b = 0 ÷ 1,α0 =1,b=0,5)
2) исп-уя эти знач-я, найдем теоретич. знач-я 
и вычислим 
3) вычислим 
4)сделаем небольшой шаг по параметру α: Δ α =1+0,1= 1,1 и снова найдем величину μ(2). Если μ(2)< μ(1) , то шаг сделан в правильном направлении.
5) продолжаем увелич-ть α в дан. напр-ии по шагам до тех пор, пока μ не начнет расти.
6) аналогич-ую процедуру проводим с параметром b фиксиров. α.
7) фиксируем найденное b и снова начинаем изменять α. Процедура повтор-ся до тех пор, пока любые измен-ия α и b не будут приводиь к увнлич-ю μ.
