Под определенным интегралом функции f (x)на отрезке [ a, b ] чаще всего понимают площадь криволинейной фигуры под графиком функции f (x) (рис. 1). Предполагается, что отрезок от a до b разбит на множество маленьких интервалов величиной h, и вычислены площади i -х столбцов Si = f (xi) . h, тогда можно с заданной точностью определить значение площади криволинейной трапеции, ограниченной графиком функции f (x)и равной сумме площадей элементарных интервалов.

Рис. 1. Геометрическая интерпретация определенного интеграла
Для вычисления определенного интеграла непрерывной функции f (x)на отрезке [ a, b ] применяют формулу Ньютона-Лейбница
 , (1)
, (1)
где F (a), F (b)– первообразные функции от подынтегральной функции F (x) = f `(x). Однако использовать формулу (1) в большинстве случаев невозможно. Для многих функций f (x)первообразную F (x)сложно определить. Кроме того, функция f (x)может быть задана не аналитически, а таблично. В этом случае используют приближенные формулы для вычисления интеграла.
Численное интегрирование широко применяется в практических расчетах, учитывая простую реализацию на компьютере и разнообразие реальных функциональных зависимостей, не описываемых элементарными функциями, заданными таблично и др.
Существует несколько методов численного интегрирования. Наиболее известные из них методы прямоугольников (4), метод трапеции (6) и метод Симпсона. Сформулируем общую постановку задачи.
1. Постановка задачи
Пусть требуется вычислить
 (2)
(2)
на отрезке [a, b], если известно, что a и b – нижний и верхний пределы интегрирования, а функция f (x) непрерывна на интервале [a, b].
2. Метод прямоугольников
Согласно общему подходу численного интегрирования интервал [a, b] разделяют на n участков длиной
 . (3)
. (3)
На каждом участке [xi, xi+1] заменяют подынтегральную функцию горизонтальной прямой и определяют площадь элементарного прямоугольника Si = f (xi).
Обобщенная формула для приближенного вычисления определенного интеграла методом левых прямоугольников имеет вид
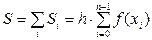 . (4)
. (4)
Замена реальной функции f (x)уравнением прямой на участках интегрирования вносит определенную погрешность в вычисление интеграла. Погрешность будет уменьшаться при увеличении количества разбиений интервала за счет более точной аппроксимации подынтегральной функции. Очевидно, что при
 . (5)
. (5)
Погрешность вычисления определенного интеграла методом
прямоугольников по формуле (4) пропорциональна шагу интегрирования h.
3. Метод трапеций
Более точно вычислить определенный интеграл можно с помощью метода трапеций. Подынтегральная функция f (x) разбивается на n равных участков, которые заменяются прямыми, соединяющими точки со значениями функции на границах каждого элементарного участка аппроксимации f (xk), f (xk+ 1). Сумма площадей образованных таким образом трапеций (рис. 1) при том же значении n точнее приближает значение интеграла к истинному, по сравнению с методами прямоугольников.
Интегральная сумма метода трапеции может быть рассчитана по одной из равносильных формул:
 (6)
(6)
 .
.
Погрешность метода трапеций (6) пропорциональна h2.
Приложение 6
Блок-схемы в Word
Вар. 1.

| Вар. 3.

|
Вар. 2.

|
Вар. 4.

|
Приложение 7
Примерный вариант
Контрольной работы Word
1. Исходный текст с помощью MS Word отформатируйте в соответствии с приведенным заданием.
2. Оформите первый лист документа как титульный, на котором введите название документа (размер шрифта – 35 пт., интервал – разреженный на 2,5 пт.). Добавьте объект WordArt –  (подобрать палитру, поместить за текстом).
(подобрать палитру, поместить за текстом).
3. Для текстовой части документа установите стиль оформления: шрифт – Arial; 14 пт.; интервал между символами обычный; межстрочный интервал множитель 1,4; выравнивание по ширине страницы, автоматическая расстановка переносов.
4. Выделите и озаглавьте разделы документа. Установите красную строку с отступом 1,25 см.
5. Для заданных слов во всем тексте установите шрифт жирный, разреженный на 2 пт. (использовать правка/замена).
6. Выделенный раздел оформите многоуровневым списком.
7. Создайте верхние колонтитулы на всех страницах документа, за исключением первой страницы (название документа). На титульном листе создайте нижний колонтитул, содержащий вашу фамилию.
8. Часть документа оформите в три колонки.
9. Одну страницу расположите на альбомных листах.
10. Вставьте в документ рисунки, расположив их в тексте. Сделайте надписи.
11. Установите сквозную нумерацию страниц, начиная со второй. Подготовьте документ к печати. Установите следующие параметры страницы: верхние и нижние поля – 2 см., левое поле – 3 см., правое – 1,5 см., отступ от колонтитула – 1 см.
12. Оформите и отредактируйте таблицу согласно заданию.
13. Вставьте в документ заданные нумерованные формулы.
14. Составьте автоматически обновляемое оглавление полученного текста.
15. Составьте список иллюстраций.
Учебное издание






