MICROSOFT WORD – один из наиболее распространенных текстовых редакторов, созданный фирмой Microsoft Corp., программа, которая позволяет набирать, исправлять, форматировать и распечатывать текст. В технологии расположения рисунка под текстом используются: Выделение, далее Выбор объекта, операция Порядок, выбор варианта расположения текста относительно рисунка.
Газетный стиль текста
M ICROSOFT WORD – один из наиболее распространенных текстовых редакторов, созданный фирмой Microsoft Corp., программа, которая позволяет набирать, исправлять, форматировать и распечатывать текст. Оформим текст в газетном стиле с буквицей. Формат газетного стиля для выделенного фрагмента текста задается с помощью последовательности команд Разметка страницы, Колонки, затем устанавливаются параметры варианта газетного текста. Для оформления буквицы используют команду Вставка, Буквица.
Приложение 2
Шрифты Word
Использовать для текста шрифт.
(Garamond, 12, обычный, красный)
Использовать для текста шрифт.
(Impact, 10, обычный, двойное синее подчеркивание).
Использовать для текста шрифт.
(Mistral, 13, с тенью, интервал разреженный 1,3 пт)
Использовать для текста шрифт.
(Verdana, 14, курсив, приподнятый)
Использовать для текста шрифт .
(Raavi, 9, полужирный курсив, Зачёркнутый, зелёный)
Написать Н2О и y = x 3.
Н2О (полужирный, обычный, 2 – нижний индекс)
y = x 3 (13, латиница – курсив, 3 – верхний индекс)
 |
Приложение 3
МНОГОУРОВНЕВЫЙ СПИСОК
1. Многие операции выполняют над выделенными фрагментами текста.
1. Способы выделения фрагмента текста:
2. С помощью клавиш:
3. Установить курсор в начало выделения;
3. Нажав клавишу Shift, перемещать курсор.
2. С помощью мыши:
4. Для отдельных символов, слов, строк текста —
5. Установите указатель мыши в начало выделения и, держа нажатой левую кнопку, протащите мышь до конца выделяемого фрагмента;
4. Для прямоугольного фрагмента —
5. Установите указатель мыши в начало выделения, при нажатой клавише Alt и левой кнопке мыши протяните мышь как по горизонтали, так и по вертикали;
4. Для отдельного слова —
5. Установите указатель мыши на слово и произведите двойной щелчок левой кнопкой мыши;
4. Для отдельного абзаца —
5. Установите курсор в произвольное место абзаца и произведите тройной щелчок левой кнопкой мыши;
4. Для одной строки —
5. Одинарный щелчок левой кнопкой мыши слева от строки текста;
4. Для группы строк текста —
5. Щелкните левой кнопкой мыши слева от начала текста и протяните мышь до конца фрагмента по вертикали;
4. Для объекта (рисунка, формулы, диаграммы) —
5. Установите курсор на объекте и щелкните левой кнопкой мыши.
1. Выделение текста всего документа выполняется с помощью команды
3. Главная \ Редактирование \ Выделить \ Выделить все.
МНОГОУРОВНЕВЫЙ СПИСОК
1. Многие операции выполняют над выделенными фрагментами текста.
2. Способы выделения фрагмента текста:
2.1. С помощью клавиш:
2.1.a. установить курсор в начало выделения;
2.1.b. нажав клавишу Shift, перемещать курсор.
2.2. С помощью мыши:
- для отдельных символов, слов, строк текста —
· установите указатель мыши в начало выделения и, держа нажатой левую кнопку, протащите мышь до конца выделяемого фрагмента;
- для прямоугольного фрагмента —
· установите указатель мыши в начало выделения, при нажатой клавише Alt и левой кнопке мыши протяните мышь как по горизонтали, так и по вертикали;
- для отдельного слова —
· установите указатель мыши на слово и произведите двойной щелчок левой кнопкой мыши;
- для отдельного абзаца —
· установите курсор в произвольное место абзаца и произведите тройной щелчок левой кнопкой мыши;
- для одной строки —
· одинарный щелчок левой кнопкой мыши слева от строки текста;
- для группы строк текста —
· щелкните левой кнопкой мыши слева от начала текста и протяните мышь до конца фрагмента по вертикали;
- для объекта (рисунка, формулы, диаграммы) —
· установите курсор на объекте и щелкните левой кнопкой мыши.
3. Выделение текста всего документа выполняется с помощью команды
3.1.a. Главная \ Редактирование \ Выделить \ Выделить все.
Приложение 4
Формулы в word
Вар. 1.
 
|
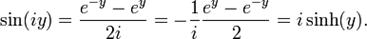
Вар. 2.
|
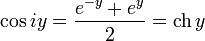
Вар. 3.
 
|
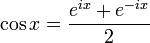
Вар. 4.
 
|
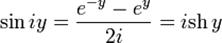
Вар 5.
 
 
|
Приложение 5
Фрагменты текста
Вариант 1
Аппроксимация первой и второй производных
через конечные разности
Вспомним определение первой производной. Если f (x) – функция одной переменной и x 0 Î [ a, b ], то функцию f ¢(x) можно записать
, (1)
где x0 – фиксированная точка.
Геометрическая интерпретация показана на рис. 1. Пусть на графике функции fзаданы фиксированная точка P0 [x0, f (x0)] и подвижная точка P [x, f (x)], и секущая, проведенная через эти точки, образует угол b с положительным направлением оси x.
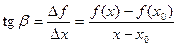. (2)
Рис. 1. Геометрическая интерпретация первой производной
Разностное отношение функции f в точке x0 равно угловому коэффициенту секущей, проведенной через точки P и P0.
Функция f называется дифференцируемой в точке x0Î[ a,b ], если существует предел разностного отношения функции в точке x0:
. (3)
Предел (3) называется производной функции f в точке x0 и обозначается
. (4)
Производная функции f в точке x0 – это тангенс угла наклона касательной к графику функции f в точке P0[x0, f (x0)](рис. 1)
. (5)
Простейшая формула численного(приближенного) дифференцирования для непрерывной функции в точке x0 через конечные разности имеет вид
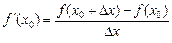(6)
или 
,
где D x=x 1 – x 0или в общем виде D x=x i – x i-1– шаг дифференцирования, величина которого должна быть достаточно малой.
Если производная функции f / (4) дифференцируема в точке x0, то 
называется второй производной функции fв точке x0 и обозначается одним из приведенных способов
. (7)
Формула численного нахождения второй производной
(8)
При подстановке в (8) выражения для нахождения первой производной получим
(9)
или 
.
При численном дифференцировании исходят из того, что функция f (x) задана конечной последовательностью пар значений (x i , fi) без помехи, и приближенные значения величин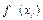 
и 
находят по формулам (6) и (9).
Вариант 2
