Динамічний режим у схемі виникає під дією змінних у часі сигналів, які подаються ззовні або виробляються в самій схемі.
5.1. Явна форма моделі
(22 а,б)
(22 а) – нормальна система звичайних диференціальних рівнянь (ЗДР).
5.1.1. Методика одержання нормальної форми ЗДР
Нехай є системи компонентних та топологічних рівнянь, причому компонентними рівняннями реактивних елементів служать диференціальні залежності:
(23)
1-й етап. На основі законів Кірхгофа змінні IC, UL записують через струми та напруги інших віток:
(24)
2-й етап. IC та UL заміняються похідними, згідно з (23), законів К. та компонентних рівнянь і передаються через IL та UC. Одержимо нормальну систему:
– нормальна система.
Приклад.
1-етап: iC = iR-IL, UL=UC
2-й етап: UR=R*iR 
Остаточно отримаємо:
Цей метод ще називається методом змінних стану.
Ємнісні контури та індуктивні зірки – топологічні виродження, так як одна з ємностей контуру (
) або одна з індуктивностей зірки (
) не може бути використана для одержання незалежного диференціального рівняння. N=NC+NL-NT – порядок нормальної системи, де NT – кількість топологічних вироджень.
Приклад.
N = 4
Виродження усувається під’єднанням до ємнісного контуру малого опору R або паралельно до індуктивності – малої провідності G. Розрахунки ускладнюються, оскільки потрібно розв’язати ще рівняння на зразок (22 б).
5.1.2. Організація розрахунку моделі схеми в явній формі
(22 а) та (22 б) розраховуються довільними числовими методами. Організація розрахунку (22 а,б) полягає в почерговому розв’язку системи (22 а) та (22 б). Нехай зі статичного режиму відомі 
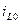та 
. Тоді:
1) підставляючи 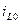та в (22 а) і розв’язуючи її будь-яким чисельним методом, визначаємо 
та 
,
2) вважаючи та , постійними джерелами струму та напруги розраховуємо квазістатичний режим, тобто (22 б) і визначаємо 
. Потім знову переходимо до п.1.
Приклад.
(а,б)
Нехай відомі 
, 
. Тоді з (а) знайдемо . Підставимо в рівняння (б) і знайдемо 
, 
, 
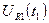. Маючи та , можемо знову розв’язати (а) відносно 
і т.д.
Основні числові методи розв’язку системи ЗДР
, 
– початкова умова. (25)
У результаті розв’язку одержимо: 
, 
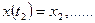
(26)
Найпростішим методом розв’язування (26) є узагальнений двоточковий метод:
, 
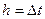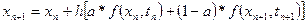(27)
При а=1 – явний метод Ейлера:
При а=0 – неявний метод Ейлера:
При 
– метод трапецій:
Приклад.
, Нехай 
Тоді явний метод: 
,
У неявниму методі: 
Неявний метод дуже стійкий, явний має обмеження на крок інтегрування 
.
5.2. Неявна форма математичної моделі
У загальному випадку маємо:
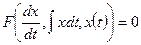, i=1,2,..,n (28)
Використаємо кінцево-різницеві апроксимації (дискретизація).
, 
(29)
Отже, від системи (28) переходимо до системи кінцево-різницевих алгебраїчних рівнянь:
(30)
Операції (29) – дискретизація. Підстановка (29) в (28) і одержання (30) – алгебраїзація.
Дискретизація і алгебраїзація – суть побудови моделі в неявній формі.
Одержана модель (30) розв’язується відносно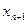 
довільним числовим методом (наприклад методом Ньютона):
(31)
, 
- матриця Якобі. Процес повторюємо, поки не пройдемо весь інтервал А.
Особливості неявної форми моделі схеми
1.Немає числового методу розв’язку (типу (26))
2.Система (28) – змішана (
, 
, і т. д.)
3.Система (28) не накладає обмежень на тип змінних (
).
5.2.1.Розрахунок неявної форми моделі схеми в базисі вузлових потенціалів.
Рівняння компонентів повинні мати вигляд 
, тобто
, 
(32)
Здійснивши операції дискретизації (в неявному методі) формул (32) (див. розділ 3.1. та рис.(3-4)), одержимо:
У загальному випадку ці формули мають вигляд:
(33)
У базисі вузлових потенціалів теоретична модель схеми для алгоритму (31) має вигляд:
(34)
При формуванні вектора струмів в (34) кожне з рівнянь для 
(33) розглядається як рівняння струму відповідної вітки. При цьому 
, 
Замінюємо через різниці потенціалів, а 
, 
...вважаємо відомими. При формуванні матриці вузлових провідностей G внесок ємнісної вітки дорівнює 
, індуктивної – 
з відповідними знаками.
Таким чином, у базисі вузлових потенціалів формування моделі схеми (34) для розрахунку перехідних процесів не відрізняється від формування моделі (21) для розрахунку статичних режимів.
Приклад.
, 
; 
;
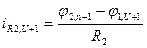
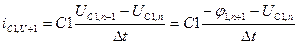Матриця вузлових струмів має вигляд
Матриця вузлових провідностей має вигляд
5.3. Моделювання частотних характеристик
Амплітудно-частотна характеристика (АЧХ):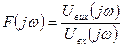 
Способи розрахунку АЧХ:
1. Аналітичний: 
, де M,N – многочлени;
2. Моделювання АЧХ на ЕОМ. При цьому є символьний підхід (коефіцієнт многочленів у вигляді формул) та чисельний підхід (розраховуються чисельні значення 
при різних 
).
Метод вузлових потенціалів дозволяє формувати вузлові рівняння і для частотної області. Методика та ж сама, змінюються лише компонентні рівняння реактивних віток, а саме:
, 
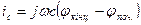(35)
Відповідно провідності реактивних віток дорівнюють
, 
(36)
Формула (35) використовується при формуванні вектора вузлових струмів, а (36) – при формуванні матриці вузлових провідностей. У схемі заміщення джерела напруги Е закорочуються, а джерела струму I – розмикаються. Одержимо вузлове рівняння лінійної схеми в частотній області:
(37)
Рівняння (37) на кожній частоті треба розв’язувати тільки один раз (на відміну від (34)).
Підставляючи в (37) різні 
і вираховуючи 
, одержимо комплексну частотну характеристику РЕП.
Якщо треба розрахувати характеристику в k-му вузлі схеми, на кожній треба вибрати з вектора 
комплексне значення потенціалу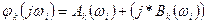 
і розрахувати АЧХ і ФЧХ у вузлі “k” за формулами
, 
(38)
