Моделювання – абстрагування від конкретного об’єкта та заміна його або фізичним аналогом, або математичним описом поведінки. Метод схеми заміщення – заміна елементів РЕА еквівалентними схемами (складні процеси та паразитні ефекти моделюються опорами (R), ємностями (С), індуктивностями (L), джерелами струму (І0) та напруги (U0)). Кінцева мета математичного моделювання РЕП – визначення струмів та напруг в усіх точках схеми протягом усього часу (після розв’язку складеної системи рівнянь).
Аналіз РЕП здійснюється в статичних та динамічних моделях.
3.1. Моделювання пасивних елементів
3.1.1. Опір. 
, 
– математичні моделі R=R(T,U,I)
3.1.2. Джерела струму та напруги.
Rвнутр→∞ Rвнутр→0
Схеми заміщення джерела струму (I0) та напруги (U0).
Групи джерел: 1. Незалежні; 2. Залежні; 3. Керовані.
3.1.3. Ємність.
, q=C·U. Частотна область:
(2)
– математична модель. Часова область: 
(3) – для математичного опису одержимо диференціальне рівняння.
 |
Машинний метод:
(4) – різницеве співвідношення
, 
(відома величина з розрахунків на попередніх трьох кроках, оскільки 
задається як початкова умова). Тоді 
(5) – одержали різницеву модель ємності у вигляді схеми заміщення.
 |
Uk
Рис.3. Схема заміщення ємності.
3.1.4. Індуктивність.
, 
. Частотна область:
. (6)
– математична модель. Часова область:
(7) – математична модель у диференціальній формі.
Машинний метод:
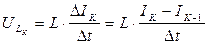(8)
– задається, тому Ік-1 – відома величина з попередніх розрахунків. 
– провідність. Тоді при 
(9)– різницева модель індуктивності.
 |
Рис.4. Схема заміщення індуктивності.
 |
3.1.5. Напівпровідниковий діод.
(10)
Інерційність процесів в р - п - переході визначається накопиченням неосновних носіїв:
– змінна складова струму через р - п - перехід.
Q – сумарна зміна заряду неосновних носіїв в р - п - переході.
τ – ефективний час життя неосновних носіїв. Тоді
,
де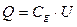 
, 
r – диференційний опір р - п - переходу, який можна визначити з вольт-амперної характеристики:
,
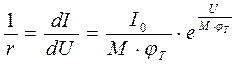тоді 
– дифузійна ємність. (11)
Вводиться 
– бар’єрна ємність. (12)
Зважатимемо ще на два фактори: 1) частина напруги Ug падає на об’ємних опорах р - п - переходу, причому rn-обл.» rр-обл і rn-обл ≡ rбази , а rр-обл=0; при оберненому зміщенні треба враховувати струм через опір поверхневого витоку Rвит.; rб і Rв вважаються лінійними.
Рис. 5. Схема заміщення напівпровідникового діода.
Математична модель діода – єдине диференціальне співвідношення із змінними Іg та Ug. У статичній моделі Сg=Cб=0.
3.2. Моделювання активних елементів
Способи моделювання транзисторів: 1. Пасивні двополюсники та керуючі джерела; 2. Багатополюсники.
Групи моделей транзисторів: 1. Нелінійні статичні; 2. Нелінійні динамічні; 3. Лінійні низькочастотні; 4. Лінійні високочастотні.
Види підходів до моделювання: 1. Формальне зображення у вигляді “чорного ящика”; 2. Побудова моделей на основі опису фізичних процесів в активному елементі.
(13)
Рис. 6. Нелінійна статична модель (Еберса Мола).
, 
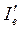– струм емітерного та колекторного переходів (описуються вольт-амперними характеристиками).
αN, αI – коефіцієнти прямої та оберненої передачі струму (за схемою з спільною базою). Отже (13) – статичні ВАХ, на основі яких можна побудувати математичну модель.
Рис. 7. Нелінійна динамічна модель (Еберса-Мола).
Rе , Rк , Rб враховує опори відповідних областей, а Се ,Ск моделює динамічні процеси, причому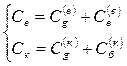 
Моделі Еберса-Мола широко застосовуються (точність – 10-15%).
Рис. 8. Лінійна низькочастотна модель (формальне зображення)
(14)
Це схема заміщення зі спільним емітером.
Коефіцієнти hік мають конкретний фізичний зміст (вхідний опір, вихідна провідність і т.д.) та знаходяться з диференціювання відповідних рівнянь за певних умов.
Рис. 9. Т-подібна лінійна високочастотна модель.
β визначає крутизну вихідного генератора струму
.
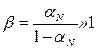Се ,Ск – моделюють інерційність транзистора, причому
Використовується наступне наближення:
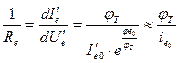, де Ue0, ie0 – статичні напруга та струм, відносно яких змінюється високочастотний сигнал.
3.3. Моделювання радіоелектронних пристроїв
Види математичних моделей РЕП: 1. Загальна схема заміщення; 2. Загальна система рівнянь для всієї схеми.
Порядок складання схеми заміщення:
1. Вибір рівнянь для опису схеми. “Первинні” внутрішні параметри – площа p-n - переходу, NA,Nф, ширина бази, μu , μр і т.д. (для підприємств, які працюють із пристроями в інтегральному виконанні). Вторинні внутрішні параметри – вхідний та вихідний опори, коефіцієнти підсилення, крутизна ВАХ і т.д. (для підприємств, які працюють із окремими елементами).
Отже, вибір рівнянь та коефіцієнтів залежить від типу промислового підприємства.
2. Вибір схеми заміщення для нелінійного елемента.
– джерело струму, 
– джерело напруги,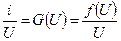 
– нелінійна провідність і.т. д.
Вибирається та схема заміщення, яка найбільше узгоджується з системою зовнішніх параметрів і дає однозначну залежність між струмом і напругою елемента.
3. Вибір системи зовнішніх параметрів.
Незалежні змінні схеми – зовнішні параметри елементів (відносно них складаються рівняння схеми).
Компонентні рівняння – описують залежності між параметрами окремих елементів (, 
і т.д.).
Топологічні рівняння – залежать від топології з’єднань і описують залежності між окремими елементами (складаються на основі законів Кірхгофа)
Нехай схема має “В” віток, “Y” – вузлів та “К” контурів. Усього “2·В” невідомих, отже система має мати “2·В” рівнянь, причому “В” компонентних, “В” топологічних (“Y-1” – за І законом К., “В-(Y-1)”– за другим законом К.).
Загальна математична модель має вигляд:
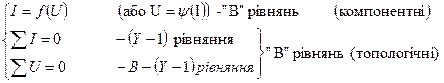
Системи незалежних змінних треба вибирати так, щоб кількість рівнянь була мінімальною. Перший крок – підстановка компонентних рівнянь у топологічні (тобто виключення струмів або напруг).
Одержуємо метод рівнянь К. для струмів:
(15)
або метод рівнянь К. для напруг:
(16)
“В” напруг, або “В” струмів після розв’язку систем (15) або (16) визначаються з відповідних компонентних рівнянь. Другий крок – вибір таких топологічних змінних, які перетворюють ряд рівнянь у тотожності. Це вузлові потенціали та контурні струми.
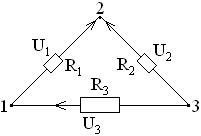
=0
0=0 – одержали тотожність.
Отже, при виборі вузлових потенціалів з системи (16) залишиться (Y-1) рівняння відносно вузлових потенціалів φ: 
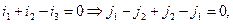
0=0 – одержали тотожність
Отже, вибравши як незалежні змінні контурні струми із системи (15) залишається В-(Y-1) рівняння відносно контурних струмів j: 
.
Для зменшення кількості рівнянь зрозуміло, що при (Y-1)<B-(Y-1) застосовуємо метод вузлових потенціалів, при В-(Y-1)<(Y-1) – метод контурних струмів.
4. Складання математичної моделі схеми.
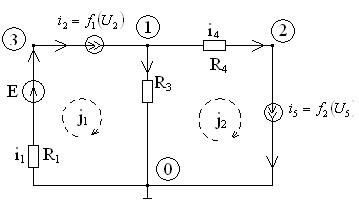
Нумеруємо всі вузли схеми. Нумеруємо всі напруги та струми. Вибираємо опорний вузол (вузол відліку). Потенціал його звичайно вважається нульовим, φ=0. Знаходимо ψ1(і2) та ψ2(і5) – обернені залежності до f 1(U2) та f 2(U5). Вибираємо напрями струму в усіх вітках і вважаємо, що струм тече від більшого потенціалу до меншого. Тепер можна складати математичну модель схеми.
Запишемо системи компонентних і топологічних рівнянь.
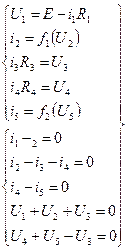
За методом рівнянь для напруг одержимо:
За методом рівнянь для струмів одержимо:
Вибравши як незалежні змінні вузлові потенціали отримаємо:
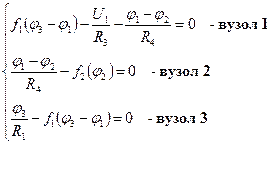
Метод контурних струмів дає наступну систему:
Топологічні рівняння схеми повинні бути лінійно незалежними – тоді розв’язок математичної моделі буде єдиним (тому маємо (Y-1) рівняння за І законом К. і В-(Y-1) – за ІІ законом К.)
3.4. Основні топологічні співвідношення
 |
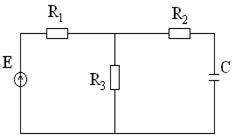
а) б) в)
Рис.10. Схема (а), граф (б), її дерево графа (в).
Граф – сукупність відрізків довільної форми й довжини, які називаються вітками, і точок їх перетину, які називаються вершинами. Контур – довільний замкнутий шлях у графі, який не проходить двічі по одних вітках. Підграф – довільна сукупність віток і вершин графа. Дерево графа – підграф, який має всі вершини графа, але не має жодного контуру. Ребро – вітка, яка належить до дерева графа. Хорда – вітка, яка не належить до дерева графа. Доповнення дерева графа – вся сукупність хорд. Головний контур – контур, який утворюється при підключенні хорди до дерева.
Якщо у схемі “В” – віток, “Y” – вузлів, то дерево графа має (Y-1) – ребро. Кількість хорд тоді В-(Y-1) (стільки ж головних контурів).
3.4.1. Топологічні матриці інциденцій та вузлів
Топологічна матиця схеми – запис інформації про з’єднання елементів у схемі в матричній формі (див. рис. 10)
Рядки матриці – вузли, графа, стовпці – вітки, причому елементи матриці:
+1 – вітка входить у вузол; -1 – вітка виходить; 0 – вітка та вузол не з’єднані. Одержана матриця називається матрицею інциденцій (з’єднань), або структурною.
Матриця вузлів містить “В” стовпців та (Y-1) рядків (рядок опорного вузла викреслюємо, тоді одержиться незалежна система рівнянь). З допомогою матриці вузлів можна записати:
- І закон К., 
- ІІ закон К.
